Axiomes de Hilbert

Dans un mémoire paru en 1899, Les fondements de la géométrie ((de) Grundlagen der Geometrie), David Hilbert propose une axiomatisation de la géométrie euclidienne. Ce sont ces axiomes, qui ont été révisés au cours des éditions successives par Hilbert lui-même, ou des axiomes directement inspirés de sa présentation que l'on appelle axiomes de Hilbert.

David Hilbert

Hilbert se situe dans la lignée d'Euclide et de ses Éléments, qui du point de vue de la rigueur ne satisfont plus les géomètres du XIX^e siècle, car pour démontrer rigoureusement les théorèmes associés à cette géométrie, il est nécessaire d'admettre comme vraies des hypothèses supplémentaires laissées implicites par Euclide.

Hilbert établit un système d'axiomes simples, qu'il répartit en plusieurs groupes, dont il analyse la portée, les théorèmes qu'ils permettent de démontrer, et ceux qui ne peuvent être obtenus sans ce groupe d'axiomes. Son objet est, ainsi qu'il le présente dans son introduction, « l'analyse de notre intuition de l'espace ».

Les axiomes de Hilbert apparaissent souvent comme la version axiomatique moderne qui permet une fondation rigoureuse de la géométrie d'Euclide. Il existe cependant d'autres axiomatisations de la géométrie élémentaire (dont les objectifs sont en partie différents) comme celle de Tarski ou celle de Birkhoff (en).

Contexte

Angles et longueurs chez Euclide

Preuve d'Euclide

Pour une image fixe, cliquer sur la flèche

Pour une animation, cliquer sur la flèche

Euclide définit dans sa géométrie les notions de longueur et d'angle. Il est intéressant de voir ce qu'Euclide présuppose implicitement lorsqu'il les utilise.

Les définitions d'angle, d'angle droit, d'angle obtus, d'angle aigu, apparaissent dès les premières définitions du Livre I des Éléments.

Un angle plan est l'inclinaison mutuelle de deux lignes qui se touchent dans un plan, et qui ne sont point placées dans la même direction.

Lorsque les lignes, qui comprennent ledit angle, sont des droites, l'angle se nomme rectiligne.

Lorsqu'une droite tombant sur une droite fait deux angles de suite égaux entre eux, chacun des angles égaux est droit.

L'angle obtus est celui qui est plus grand qu'un droit.

L'angle aigu est celui qui est plus petit qu'un droit.

Cependant Euclide ne précise pas comment il définit l'égalité ou la comparaison de deux angles, pas plus qu'il ne définit l'égalité de deux longueurs. En fait, il apparaît qu'Euclide utilise implicitement la conservation des angles ou des longueurs de segments lorsque ceux-ci sont déplacés d'une position à l'autre, même si la notion de déplacement n'apparaît pas non plus explicitement dans les Éléments. Ainsi, pour montrer qu'un triangle ABC, ayant deux côtés AB et AC de même longueur, est tel que les angles B et C sont égaux, Euclide superpose les triangles ABC et ACB. Il suppose donc implicitement que, dans cette superposition, longueurs et angles sont conservés. La géométrie d'Euclide est donc ce qu'on pourrait appeler une géométrie des figures rigides.

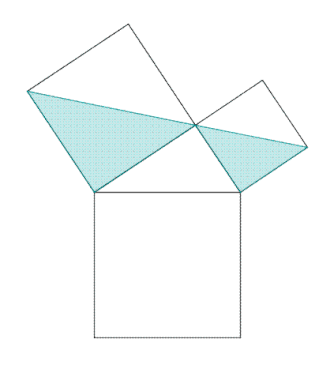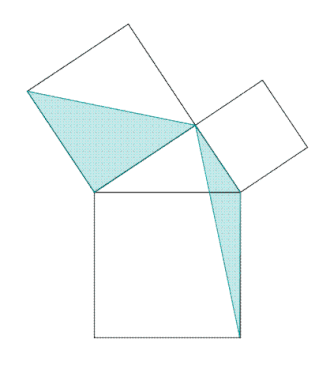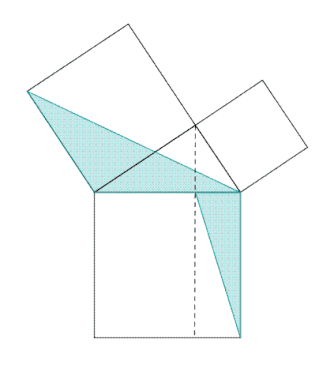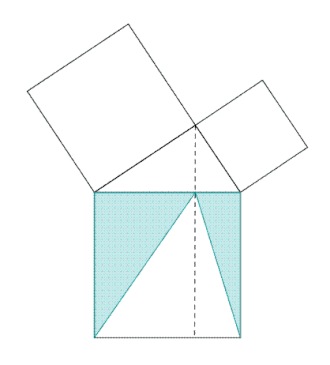
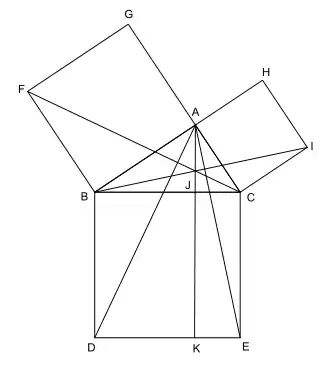
La figure du paragraphe illustre le mécanisme d'une preuve classique dans la démonstration d'un théorème, celui de Pythagore. Les triangles AEC et IBC sont semblables car le deuxième est la rotation d'un quart de tour du premier. Un triangle est donc une figure rigide qui possède une aire invariante par rotation.

Théorie des proportions

Le livre V des éléments d'Euclide introduit une théorie des proportions entre grandeurs de même nature (longueur, aires, volumes). Cette théorie, attribuée à Eudoxe de Cnide par Archimède, qui ne fait jamais référence à Euclide, permet de traiter les proportions entre grandeurs incommensurables, ce que nous appelons aujourd'hui les nombres irrationnels, comme l'a illustré en particulier Archimède. Les proportions des grecs n'ont pas vraiment le statut de nombre, les opérations doivent avoir un sens géométrique. Elles peuvent être multipliées ou divisées par un nombre entier.

Hilbert établit une théorie des proportions (voir plus loin) où celles-ci ont le statut de nombre à part entière.

Géométries non euclidiennes

Une géométrie non euclidienne

Une idée fréquente pendant plus des deux millénaires qui ont suivi l'édition des Éléments d'Euclide est le fait qu'il n'existe que deux uniques géométries, celle du plan euclidien, et celle de l'espace euclidien.

Elle se traduit par le statut donné au cinquième postulat, dit de la parallèle. Tel que formulé par Proclos, celui-ci stipule que « dans un plan, par un point distinct d'une droite d, il n'existe qu'une unique droite parallèle à d.» Si, comme on l'a cru jusqu'au début du XIX^e siècle l'unicité de la géométrie euclidienne est vraie, alors le cinquième postulat ne serait qu'un théorème, encore à l'état de conjecture. Il ne manquerait que le talent d'un mathématicien pour la démontrer, mais la proposition serait vraie et son statut de postulat ne serait que provisoire.

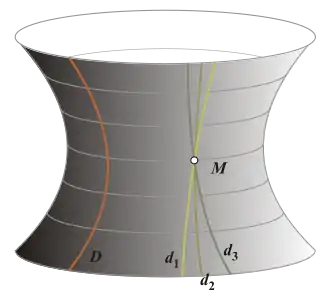
Il existe une infinité de droites qui, comme d1, d2 et d3, passent par le point M et sont parallèles à la droite D. Exemple de géométrie hyperbolique ne respectant pas le 5^e postulat d'Euclide.

Mais lorsque Hilbert axiomatise la géométrie euclidienne, on sait déjà qu'il y a des géométries qui ne respectent pas le 5^e postulat. Dans son programme d'Erlangen, Felix Klein ordonne les différentes géométries : les espaces de Nikolaï Lobatchevski et Bernhard Riemann ne vérifient pas le 5^e postulat.

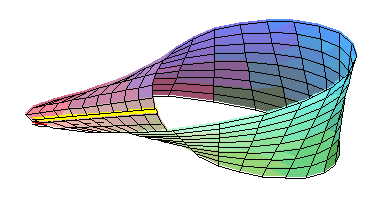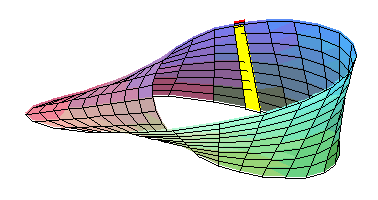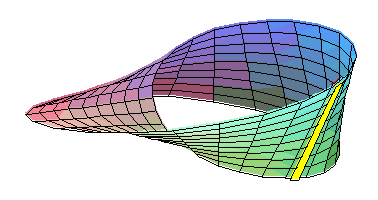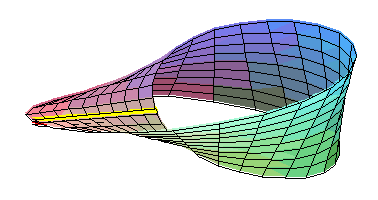
D'autres cas sont connus : Klein a construit un espace, celui de la figure qui respecte le cinquième postulat, mais qui n'est pas orientable. Dire qu'un espace est « orientable » signifie que la droite et la gauche existent. Dans un espace euclidien, une main droite et une main gauche ne sont jamais superposables, il est impossible de les faire coïncider sans utiliser une symétrie, c’est-à-dire une transformation équivalente à celle d'un miroir. La figure du paragraphe montre que cet état de fait n'est pas vrai dans toutes les géométries. Ainsi, la règle de la figure, jaune sous le plan et rouge au-dessus, par un mouvement continu devient rouge sous le plan et jaune au-dessus. Ce qui est impossible dans un plan euclidien.

Analyse de Hilbert

Ces présuppositions ont été mises en évidence à la fin du XIX^e siècle par Pasch et Hilbert. Celui-ci a donné, avec Les fondements de la géométrie, un exposé axiomatique complet et rigoureux, s'attachant à clairement identifier tous les axiomes implicitement utilisés dans la géométrie traditionnelle.

Angle et longueur

Une des notions fondamentales de la théorie d’Euclide est donc celle d’égalité, ou congruence entre figures. Deux figures sont égales si elles peuvent représenter deux positions différentes d’un même corps rigide. Pour savoir si deux distances AB et CD sont égales, on peut repérer deux points E et F sur une règle rigide, et s’assurer que EF peut être ajusté à la fois sur AB et sur CD. Cela conduit à un problème de circularité : au sens géométrique, une règle est rigide lorsque les distances entre ses points ne varient pas au cours d'un déplacement. Mais pour savoir que deux distances sont égales, on se sert d’un corps rigide qu'on déplace.

David Hilbert, dans ses Fondements de la géométrie, mettra en évidence ce cercle vicieux. Pour y remédier, il introduit de nouveaux axiomes dévoilant les présupposés implicites d'Euclide. Ces axiomes donnent les propriétés qu'on souhaite voir vérifiées par des figures congruentes. Par exemple, on souhaite que la règle de transitivité soit respectée : si AB et CD ont la même longueur, et que CD et EF ont aussi la même longueur, alors AB et EF doivent avoir même longueur. Par ailleurs, un des axiomes de Hilbert relie congruence de segments et congruence d'angles et constitue le premier cas d'égalité des triangles : si [AB] est congruent à [A'B'], [AC] à [A'C'] et l'angle BAC à l'angle B'A'C', alors [BC] est congruent à [B'C']. À noter que cette propriété, qui est un théorème chez Euclide, est devenue un axiome chez Hilbert. C'est qu'Euclide suppose implicitement que les déplacements conservent la congruence. Cette supposition, mise à jour par Hilbert, revient en fait à admettre la validité du théorème. Hilbert déduit de cet axiome les autres cas d'égalité des triangles, l'existence de l'angle droit et la congruence entre eux de tous les angles droits, cette dernière propriété étant un axiome chez Euclide.

Nombre et géométrie chez Hilbert

Le choix axiomatique de Hilbert, ne fait pas appel aux nombres. Des deux axiomes de continuité, l'un correspond à la propriété archimédienne, l'autre à la complétude du corps des réels. Ces deux axiomes assurent que « la géométrie ainsi construite est identique à la géométrie cartésienne » (Hilbert 1971, p. 42, traduction Rossier), en particulier une droite représente la droite réelle. Le corps des réels est, en théorie des ensembles, l'unique corps archimédien complet.

Cependant Hilbert montre, au chapitre III de son ouvrage, qu'il est possible sans faire appel aux axiomes de continuité, d'« établir la théorie euclidienne des proportions ». il se fonde sur les axiomes d'incidence, d'ordre, et des parallèles (I.1 à 3), II, III et IV) de la géométrie plane, et démontre pour cela le théorème de Pappus (appelé par Hilbert théorème de Pascal, en tant que cas particulier de celui-ci). Le théorème de Pappus permet de définir un « calcul segmentaire » qui satisfait les propriétés de corps commutatif.

Au chapitre V il montre qu'il est possible d'introduire un calcul segmentaire fondé sur le théorème de Desargues, sans utiliser les axiomes de congruence (groupe III). Les axiomes d'ordre ne sont pas utilisés pour établir le calcul, mais seulement pour ordonner le système de nombre obtenu[1], dont la multiplication peut ne pas être commutative. C'est-à-dire que les axiomes d'incidence et l'axiome des parallèles, correspondent à une géométrie construite sur un corps gauche (commutatif ou non), et Hilbert montre qu'une géométrie construite sur un « système arguésien de nombres » (corps gauche ordonné) vérifie les axiomes d'incidence d'ordre et de parallélisme (voir plan affine arguésien pour une présentation modernisée due à Emil Artin).

Hilbert[2] montre que le théorème de Desargues nécessite, si on se restreint aux axiomes d'incidence et de parallélisme, d'utiliser l'espace. L'autre possibilité est d'utiliser les axiomes de congruence (c'est une conséquence du chapitre III, le théorème de Desargues étant conséquence du théorème de Pappus, par le théorème d'Hessenberg).

Géométries non archimédiennes

Hilbert montre que l'axiome du premier cas d'égalité des triangles ne peut se déduire des autres axiomes. On peut en effet définir une géométrie non-archimédienne vérifiant tous les axiomes de la géométrie de Hilbert sauf le premier cas d'égalité des triangles. Dans cette géométrie :

On ne dispose pas de l'inégalité triangulaire.
Les cas d'égalité des triangles ne sont plus valables.
On peut avoir un triangle ayant deux angles égaux, mais dont les deux côtés ne sont pas égaux.
La symétrie par rapport à une droite ne conserve pas nécessairement les longueurs.
La notion d'aire d'un triangle (base × hauteur/2) n'est plus définie.
On peut trouver deux carrés équidécomposables (i.e. qui peuvent être décomposés en triangles congruents), dont l'un est intérieur à l'autre.

Les axiomes

Hilbert présente ses axiomes en les accompagnant de théorèmes et de définitions. Ses axiomes ne sont pas conçus pour être présentés isolément. Ils utilisent certaines définitions, qui s'appuient sur des axiomes précédemment introduits, ou des théorèmes obtenus à partir de ceux-ci. Ainsi les notions de segment, de demi-droite, d'angle (de demi-droites), de triangle sont introduites au fur et à mesure de l'exposé, et ne font pas partie des notions primitives.

Hilbert introduit trois types d'objets primitifs. Ces objets ne sont pas définis, il s'agit de point, de droite et de plan.

Certaines relations entre ces objets sont décrites par les axiomes, regroupés en cinq groupes : l'incidence (ou association, ou appartenance), l'ordre, les parallèles, la congruence, et la continuité.

Les axiomes d'incidence[3] définissent être situé sur, qui correspond aux notions est élément de (pour un point vis-à-vis d'une droite où d'un plan) et est inclus dans (pour une droite vis-à-vis d'un plan). On utilise librement ces équivalents ou d'autres expressions, comme telle droite passe par tel point, tel point est sur telle droite, deux droites, ou deux plans ont un point en commun, etc.

Les axiomes d'ordre définissent la relation entre reliant 3 points, qui permet de définir les segments.

Les axiomes de congruence, définissent trois relations d'équivalence, être congruent à, pour les couples de points, les triangles et les angles.

Les points, droites et plans sont considérés comme distincts par défaut, les cas contraires sont précisés dans la suite de l'article.

I. Incidence

I.1 : Par deux points distincts, passe une droite.

I.2 : Par deux points distincts, passe une seule droite (c'est-à-dire que la droite donnée en I.1 est unique, elle est déterminée par les deux points distincts).

I.3 : Sur une droite sont situés au moins deux points, et pour une droite donnée, il existe au moins un point qui n'est pas sur la droite.

I.4 : Soient trois points non alignés c'est-dire non situés sur une même droite, alors il existe un plan sur lequel sont situés ces trois points. Sur tout plan est situé au moins un point.

I.5 : Soient trois points non alignés, il n'existe qu'un et un seul plan sur lequel sont situés ces trois points.

I.6 : Soient deux points (distincts) d'une droite d qui sont sur un plan α, alors tous les points de d sont sur α. On dit alors que la droite d est dans le plan.

I.7 : Si deux plans ont un point en commun, ils ont alors au moins un autre point en commun.

I.8 : Il existe au moins un quadruplet de points non situés sur un même plan, c'est-à-dire tels que les quatre points sont non coplanaires.

II. Ordre

II.1 : Si un point B est entre les points A et C, B est aussi entre les points C et A, et il existe une droite contenant les trois points A, B, C.

II.2 : Soient deux points A et C, il existe au moins un point B de la droite AC tel que C soit entre A et B.

II.3 : Soient trois points alignés, alors un au plus se situe entre les deux autres.

Définition : Deux points A et B sur une droite d, définissent un segment noté AB ou BA. Les points du segment AB sont les points de d entre A et B. Les extrémités du segment AB sont les points A et B.

II.4 : Axiome de Pasch. Soient trois points A, B, C non alignés et soit une droite d contenue dans le plan ABC mais ne passant par aucun des points A, B, C. Si d passe par un point du segment AB, alors d passe aussi soit par un point du segment AC, soit par un point du segment BC.

III. Congruence

III.1 : Soient deux points distincts A, B et un point A' élément d'une droite d, il existe deux et deux uniques points C et D éléments de la droite d, tel que A' se situe entre C et D, et AB est congru à CA' ainsi qu'à DA' .

III.2 : La relation de congruence est transitive, c’est-à-dire, si AB est congru à CD et si CD est congru à EF, alors AB est congru à EF.

III.3 : Soient une droite d contenant les segments sans point commun AB et BC et une droite d' contenant les segments sans point commun A'B' et B'C' . Si AB est congru à A'B' et BC est congru à B'C' , alors AC est congru à A'C' .

III.4 : Soient un angle ABC dans un plan α et une demi-droite B'C' dans un plan α', il existe deux et seulement deux demi-droites, B'D et B'E dans le plan α', telles que l'angle DB'C' est congru à l'angle ABC et l'angle EB'C' est congru à l'angle ABC.

Corollaire : Tout angle est congru à lui-même.

III.5 : Soient deux triangles ABC et A'B'C' tel que AB est congru à A'B' , AC est congru à A'C' , et l'angle BAC est congru à l'angle B'A'C' , alors le triangle ABC est congru au triangle A'B'C' .

IV. Parallèles

IV : Axiome des parallèles. Soient une droite d et un point A non sur d ; dans le plan déterminé par d et A, il existe au plus une droite passant par A qui n'a aucun point commun avec d.

De cet axiome et des précédents on déduit que par un point extérieur à une droite, il passe une et une seule parallèle à cette droite.

V. Continuité

V.1 : Axiome d'Archimède. Soient deux segments AB et CD tel que C est différent de D. Alors il existe un entier n, et n points A₁, etc., A_n de la droite contenant le segment AB, tels que A_j se situe entre A_j-1 et A_j+1 si 2 ≤ j < n - 1, A_jA_j+1 est congru à CD si 1≤ j <n - 1, A est confondu avec A₁ et B se situe entre A et A_n.

Ce groupe peut, ou non, être complété par un axiome impliquant la complétude de la géométrie. Celui-ci est ajouté par Hilbert à la traduction française de 1900 et apparaît dès la seconde édition de 1903[4]. Hilbert précise qu'il ne supposera pas en général sa validité.

V.2 : Axiome de l'intégrité linéaire. L'ensemble des points d'une droite, soumis aux relations d'ordre et de congruence, n'est susceptible d'aucune extension dans laquelle restent valides les relations précédentes et les axiomes I à III et V.1[5]

Hilbert précise que l'axiome d'intégrité permet de montrer le théorème de Bolzano sur l'existence de points d'accumulation, et la construction des coupures de Dedekind.

L'axiome apparaît sous une forme proche à partir de la 7^e édition (la dernière parue du vivant de Hilbert). Dans les éditions précédentes (sauf la première où il est absent et n'a pas d'équivalent), il est énoncé pour tous les éléments de la géométrie, points, droites et plans (« ... les éléments de la géométrie forment un système d'êtres qui, si l'on conserve tous les axiomes, n'est susceptible d'aucune extension »), énoncé qui devient un théorème de l'intégrité, déduit de l'intégrité linéaire, dans les versions suivantes[6].

Ce dernier axiome n'est pas un axiome ordinaire, il fait référence aux autres axiomes, et il s'agit plutôt d'un « meta-axiome »[7]. Hilbert fait d'ailleurs remarquer que cet axiome, en l'absence de celui d'Archimède devient contradictoire[7].

Il est possible de le remplacer par un axiome plus « usuel », mais du second ordre (faisant intervenir la notion d'ensemble), comme l'axiome de Cantor, sur les segments emboîtés d'intersection non vide (leurs extrémités comprises)[8], ou l'axiome de Dedekind, qui énonce que pour toute partition d'une droite en deux parties non vides, telle qu'aucun point de l'une de ces parties ne soit entre deux points de l'autre, il existe un point de la droite telle que l'une des parties est une demi-droite issue de ce point[9].

Commentaires

Dans l'article de 1899, Hilbert avait ajouté un 21^e axiome, qui s'est avéré redondant : il était possible de le déduire des autres. Eliakim Hastings Moore démontra cette redondance en 1902, de même que le jeune Robert Lee Moore (homonyme sans lien de parenté).

« Soient quatre points sur une droite, il est toujours possible de les nommer A, B, C, et D, tel que B est entre A et C et entre A et D. De sorte que, C se trouve entre A et D et aussi entre B et D. »

Cette base axiomatique décrit l'espace euclidien de dimension trois. Il est relativement simple de transformer les hypothèses pour décrire un espace de dimension 2.

Cette axiomatique se formalise naturellement dans un calcul des prédicats à plusieurs types d'objets, les points, les droites, et les plans, une variante du calcul des prédicats ordinaire, où on préfère séparer syntaxiquement les objets de base du modèle plutôt que de les définir par des prédicats. Les axiomes de continuité ne sont pas des axiomes de la logique du premier ordre : ils requièrent la logique du second ordre (quantifications sur des ensembles d'objets de base). Tarski a donné une axiomatisation au premier ordre de la géométrie, qui repose de fait sur la notion de corps réel clos (et non sur le corps des réels), et qui est décidable et complète, à la différence de l'axiomatisation de Hilbert.

L'intérêt de l'approche de Hilbert est plus méthodologique que pédagogique ou appliquée. En effet, dès cette époque était déjà connue l'approche algébrique par des espaces vectoriels abstraits et des produits scalaires. Son article sur les fondements n'a donc une conséquence que secondaire en géométrie. En revanche, la démarche consistant à définir une approche axiomatique non redondante, cohérente et si possible complète est avant-gardiste. L'article, durant le XX^e siècle, est d'une influence considérable sur l'approche axiomatique formelle en logique.

Modèle algébrique des axiomes de Hilbert.

Soit E un espace affine euclidien, ayant pour direction l’espace vectoriel euclidien V sur le corps des réels de dimension 3.

I Axiomes d'incidence

Nous appelons droites les sous-espaces affines de dimension 1 et plans les sous-espaces affines de dimension 2. Les points, les droites et les plans de E vérifient les axiomes d’incidence de Hilbert.

Démonstration

I.1 Soient A et B deux points. La droite d contenant le point A, et de direction W, sous-espace de V de dimension 1 engendré par le vecteur AB, contient aussi le point B.

I.2 Soit une autre droite d’ passant par A et B de direction W. Le sous-espace W’ de dimension 1 contient le vecteur AB : il est donc identique à W et d’est identique à d

I.3 Toute droite d est non-vide et contient au moins un point A. Sa direction contient au moins un vecteur v non nul, et la droite d contient aussi le point A + v.

L’espace vectoriel V étant de dimension strictement supérieure à 1 contient au moins un vecteur w n’appartenant pas à la direction de d. Le point A+w n’appartient pas à la droite d.

I.4 Soient A, B et C trois points non alignés. Les vecteurs AB et AC ne sont donc pas colinéaires et le sous-espace vectoriel Q engendré par AB et AC est de dimension 2. Le plan P contenant A et de direction Q contient aussi les points B et C.

I.5 Soit P’ un autre plan passant par A, B et C de direction Q’. Le sous-espace vectoriel Q’ de dimension 2 contient les vecteurs AB et AC : il est donc identique à Q et P’ est identique à P.

I.6 Soit A et B deux points appartenant au plan P de direction Q. Le vecteur AB appartient donc au sous-espace vectoriel Q. Soit C un autre point quelconque de la droite AB. Les vecteurs AC et AB sont colinéaires et le vecteur AC appartient aussi à la direction Q, donc C appartient au plan P.

I.7 Soit P un plan de direction Q passant par le point A, et soit P’ un autre plan de direction Q’ passant aussi par A. L’intersection de Q et de Q’ est un sous-espace vectoriel de dimension 1 ou 2. Soit v un vecteur non nul de cette intersection. Le point A + v, différent de A, appartient à la fois à P et à P’.

I.8 Soient A, B, et C trois points non alignés, et P le plan de direction Q passant par ces trois points. L’espace V étant de dimension strictement supérieure à 2, il contient au moins un vecteur w de V n’appartenant pas à Q. Le point A + w n’appartient pas au plan P.

II Axiomes d’ordre.

Soit O(A, B, C) la relation ternaire « B est entre A et C », vérifiée si et seulement s’il existe un réel r négatif tel que le vecteur ${\overrightarrow {BA}}$ soit égal au produit du vecteur ${\overrightarrow {BC}}$ par r. Muni de cette relation, E vérifie les axiomes d’ordre de Hilbert.

Démonstration

II.1 Si B est entre A et C, le vecteur ${\overrightarrow {BA}}$ est égal au produit du vecteur ${\overrightarrow {BC}}$ par r, et le vecteur ${\overrightarrow {BC}}$ est égal au produit du vecteur ${\overrightarrow {BA}}$ par 1/r. Donc B est entre C et A.

II.2 Soient deux points A et B. Il existe au moins un réel r strictement compris entre 0 et 1. Soit M le point A + r. ${\overrightarrow {AB}}$ :

${\overrightarrow {MA}}$ = -r. ${\overrightarrow {AB}}$

${\overrightarrow {MA}}$ = (-r/1-r). ${\overrightarrow {MB}}$

Donc M est entre A et B.

II.3 Soient A, B et C trois points alignés et r le réel tel que :

${\overrightarrow {BA}}$ = r. ${\overrightarrow {BC}}$

Si r est négatif, B est entre A et C.

Si r est compris entre 0 et 1 :

${\overrightarrow {AB}}$ = r. ${\overrightarrow {CB}}$

${\overrightarrow {AB}}$ = (-r/1-r). ${\overrightarrow {AC}}$

Donc A est entre B et C.

Si r est supérieur à 1 :

${\overrightarrow {CB}}$ =(1/r). ${\overrightarrow {AB}}$

${\overrightarrow {CB}}$ =(1/1-r). ${\overrightarrow {CA}}$

Donc C est entre B et A.

II.4 Dans un plan P de direction Q, étant donnés une droite d définie par un de ses point A et sa direction W, et un point B du plan P n’appartenant pas à d, un point M du plan P est dit «du côté de B (resp. du côté opposé à B) par rapport à d » si la projection du vecteur ${\overrightarrow {AM}}$ selon W sur le vecteur ${\overrightarrow {AB}}$ est positive (resp. négative)

Cette définition est indépendante du point A choisi pour définir d. Deux points M et N du plan P non situés sur la droite d sont soit d’un même côté de d, soit de côtés opposés.

Si M et N sont deux points du plan P non situés sur la droite d de côtés opposés de d, la droite MN coupe la droite D en un point A, qui est entre M et N.

En effet, la droite MN n’a pas la direction W, sinon M et N seraient du même côté de d. Elle coupe la droite d en un point A. M étant de côté opposé à N, il existe r négatif tel que :

${\overrightarrow {AM}}$ = r. ${\overrightarrow {AN}}$

Donc A est entre M et N.

Soient A, B et C trois points non alignés et soit d une droite passant par un point D entre A et B de direction W. Donc A et B sont de côtés opposés par rapport à d. Le point C est soit du côté de A, soit du côté de B par rapport à d, et donc soit du côté opposé à B, et dans ce cas d coupe BC entre B et C, soit du côté opposé à A, et dans ce cas d coupe AC entre A et C. L’axiome de Pasch est donc vérifié.

III Axiomes de congruence.

Deux segments AB et A’B’ sont dits congrus si les normes des vecteurs ${\overrightarrow {AB}}$ et ${\overrightarrow {A'B'}}$ sont égales. Une demi-droite d’origine O et de vecteur unitaire ${\overrightarrow {u}}$ est l’ensemble des points M pour lesquels il existe un réel positif ou nul r tel que : ${\overrightarrow {OM}}$ = r. ${\overrightarrow {u}}$

Un angle ${\widehat {xOy}}$ est un couple de deux demi-droites Ox et Oy de même origine.

Deux angles ${\widehat {xOy}}$ et ${\widehat {x'Oy'}}$ sont dits congrus si, ${\overrightarrow {u}}$ , ${\overrightarrow {v}}$ , ${\overrightarrow {u'}}$ et ${\overrightarrow {v'}}$ étant respectivement les vecteurs unitaires de Ox, Oy, O’x' et O’y', le produit scalaire ${\overrightarrow {u}}\cdot {\overrightarrow {v}}$ est égal au produit scalaire ${\overrightarrow {u'}}\cdot {\overrightarrow {v'}}$ .

L’espace affine E vérifie les axiomes de congruence de Hilbert.

Démonstration

III.1 Soient deux points distincts A et B et un point A’ appartenant à une droite d. Soit ${\overrightarrow {u}}$ le vecteur unitaire d’une des demi-droites d’origine A’ de la droite d. Soient C et D les points A’ + || ${\overrightarrow {AB}}$ ||. ${\overrightarrow {u}}$ et A’ – || ${\overrightarrow {AB}}$ ||. ${\overrightarrow {u}}$

${\overrightarrow {A'C}}$ = -1. ${\overrightarrow {A'D}}$ donc A’ est entre C et D

|| ${\overrightarrow {A'C}}$ || = || ${\overrightarrow {AB}}$ ||

|| ${\overrightarrow {A'D}}$ || = || ${\overrightarrow {AB}}$ ||

Si E est tel que :

${\overrightarrow {A'E}}$ = r. ${\overrightarrow {u}}$ et || ${\overrightarrow {A'E}}$ ||=|| ${\overrightarrow {AB}}$ ||

alors soit r = || ${\overrightarrow {AB}}$ || et E est confondu avec C

soit r = - || ${\overrightarrow {AB}}$ || et E est confondu avec D

III.2 Si AB est congru à CD et CD est congru à EF, les normes des trois vecteurs ${\overrightarrow {AB}}$ , ${\overrightarrow {CD}}$ et ${\overrightarrow {EF}}$ sont égales, et AB est donc congru à EF.

III.3 Soient une droite d contenant deux segments sans points communs AB et BC, et un droite d’ contenant deux segments sans points communs A’B’ et B’C’. Il existe donc deux réels positifs r et r’ tels que :

${\overrightarrow {BC}}$ = r. ${\overrightarrow {AB}}$ et ${\overrightarrow {B'C'}}$ = r’. ${\overrightarrow {A'B'}}$

Donc ${\overrightarrow {AC}}$ = (1+r). ${\overrightarrow {AB}}$ et ${\overrightarrow {A'C'}}$ =(1+r’). ${\overrightarrow {A'B'}}$

Si AB est congru à A’B’ et BC est congru à B’C’ :

|| ${\overrightarrow {AB}}$ ||=|| ${\overrightarrow {A'B'}}$ || et || ${\overrightarrow {BC}}$ ||=|| ${\overrightarrow {B'C'}}$ ||

Alors r = r’ et (1+r)|| ${\overrightarrow {AB}}$ || = (1+r’)|| ${\overrightarrow {A'B'}}$ ||

Donc AC est congru à A’C’.

III.4 Soient BC et BA deux demi-droites du plan P d’origine B et de vecteurs unitaires ${\overrightarrow {u}}$ et ${\overrightarrow {v}}$ , et soit une demi-droite B’C’ du plan P’ d’origine B’ et de vecteur unitaire ${\overrightarrow {u'}}$ . Soient ${\overrightarrow {w}}$ et ${\overrightarrow {w'}}$ des vecteurs unitaires respectivement orthogonal à ${\overrightarrow {u}}$ et orthogonal à ${\overrightarrow {u'}}$ et appartenant respectivement à la direction de P et à la direction de P’. Soient x et y les coordonnées de ${\overrightarrow {v}}$ dans la base ( ${\overrightarrow {u}}$ , ${\overrightarrow {w}}$ ). Soient ${\overrightarrow {v'}}$ et ${\overrightarrow {v''}}$ les vecteurs de coordonnées (x,y) et (x,-y) dans la base ( ${\overrightarrow {u'}}$ , ${\overrightarrow {w'}}$ ).

|| ${\overrightarrow {v'}}$ ||²= x² + y² = 1

${\overrightarrow {u}}\cdot {\overrightarrow {v}}$ = x

${\overrightarrow {u'}}\cdot {\overrightarrow {v'}}$ = x

Donc la demi-droite d’origine B’ et de vecteur unitaire v’ forme un angle avec la demi-droite congru à l’angle ${\widehat {ABC}}$ . De même la demi-droite B’ et de vecteur unitaire v’’ forme un angle avec la demi-droite congru à l’angle ${\widehat {ABC}}$ .

Soit une autre demi-droite d’origine B’ et de vecteur unitaire ${\overrightarrow {v'''}}$ , de coordonnées (x’’’, y’’’) dans la base ( ${\overrightarrow {u'}}$ , ${\overrightarrow {w'}}$ ) formant aussi un angle avec la demi-droite congru à l’angle ${\widehat {ABC}}$ .

|| ${\overrightarrow {v'''}}$ ||= 1

${\overrightarrow {u'}}\cdot {\overrightarrow {v'''}}$ = x’’’ = x

y’’’² = y²

Donc ${\overrightarrow {v'''}}$ est confondu soit avec ${\overrightarrow {v'}}$ soit avec ${\overrightarrow {v''}}$ .

III.5 Soient deux triangles ABC et A'B'C' tel que AB est congru à A'B', AC est congru à A'C', et l'angle ${\widehat {BAC}}$ est congru à l'angle ${\widehat {B'A'C'}}$ . Soient ${\overrightarrow {u}}$ , ${\overrightarrow {v}}$ , ${\overrightarrow {u'}}$ et ${\overrightarrow {v'}}$ les vecteurs unitaires respectifs des demi-droites d’origine A passant par B, d’origine A passant par C, d’origine A’ passant par B’ et d’origine A’ passant par B’.

|| ${\overrightarrow {B'C'}}$ ||²= || ${\overrightarrow {A'B'}}$ ||² + || ${\overrightarrow {A'C'}}$ ||² - 2 || ${\overrightarrow {A'B'}}$ || || ${\overrightarrow {A'C'}}$ || ${\overrightarrow {u'}}\cdot {\overrightarrow {v'}}$

|| ${\overrightarrow {B'C'}}$ ||²= || ${\overrightarrow {AB}}$ ||² + || ${\overrightarrow {AC}}$ ||² - 2 || ${\overrightarrow {AB}}$ || || ${\overrightarrow {AC}}$ || ${\overrightarrow {u}}\cdot {\overrightarrow {v}}$

|| ${\overrightarrow {B'C'}}$ ||² = || ${\overrightarrow {BC}}$ ||²

Donc B’C’ est congru à BC.

${\overrightarrow {BA}}\cdot {\overrightarrow {BC}}$ = ${\overrightarrow {BA}}\cdot {\overrightarrow {AC}}$ - ${\overrightarrow {BA}}\cdot {\overrightarrow {AB}}$

${\overrightarrow {BA}}\cdot {\overrightarrow {BC}}$ = || ${\overrightarrow {BA}}$ ||² - ${\overrightarrow {AB}}\cdot {\overrightarrow {AC}}$

${\overrightarrow {BA}}\cdot {\overrightarrow {BC}}$ = || ${\overrightarrow {B'A'}}$ ||² - ${\overrightarrow {A'B'}}\cdot {\overrightarrow {A'C'}}$

${\overrightarrow {BA}}\cdot {\overrightarrow {BC}}$ = ${\overrightarrow {B'A'}}\cdot {\overrightarrow {B'C'}}$

Donc l’angle ${\widehat {ABC}}$ est congru à l’angle ${\widehat {A'B'C'}}$ .

De même l’angle ${\widehat {ACB}}$ est congru à l’angle ${\widehat {A'C'B'}}$ , et les triangles ABC et A’B’C’ sont donc congrus.

IV Parallèles.

Si deux droites ont des directions complémentaires, elles ont un point commun.

Soit d passant par A et de direction W, et d’ passant par A’ de direction W’. Le vecteur AA’ peut être décomposé en deux vecteurs u et u’ appartenant respectivement à W et à W’.

${\overrightarrow {AA'}}$ = ${\overrightarrow {u}}$ + ${\overrightarrow {u'}}$

Les deux points A + ${\overrightarrow {u}}$ et A' - ${\overrightarrow {u'}}$ sont confondus en un point commun à d et à d’.

Donc toute droite passant par A’ et ne coupant pas d a la même direction que d. Elle est donc unique et l’axiome d’Euclide est vérifié.

V Continuité.

Pour toute droite, il existe au moins une bijection sur l’ensemble R des réels respectant l’incidence, l’ordre et la congruence. En effet, étant donné deux points distincts O et A de la droite, l’application qui fait correspondre au point P l’unique réel r tel que :

${\overrightarrow {OP}}$ = r. ${\overrightarrow {OA}}$

est une telle bijection.

La vérification par toute droite des axiomes d’Archimède et d’intégrité, résulte de la vérification par l’ensemble des réels des axiomes d’Archimède et d’intégrité.

Démonstration

V.1 Soit j+1 le plus petit entier de la classe supérieure de r : r est compris entre j et j+1 et l’axiome d’Archimède est vérifié par l’ensemble des réels.

V.2 Supposons l’existence R’ d’une extension de R satisfaisant les axiomes d’incidence, d’ordre de congruence et d’Archimède et soit m’ un élément de R’ n’appartenant pas à R. On peut repartir tous les rationnels en deux classes C’ et C’’ de la façon suivante : si sur R’ q est inférieur à m', q est dans la classe C’, et si sur R’ q est supérieur à m', q est dans la classe C’’. Ces deux classes forment une coupure de Dedekind. Soit m le réel associé à cette coupure. Le nombre m’ n’appartenant pas à R est distinct de m. Supposons m inférieur a m’. R’ satisfaisant l’axiome d’Archimède, il existe un rationnel q’ strictement supérieur à m entre m et m’. Mais q’ serait dans C’ donc inférieur à m, d’où contradiction. En supposant m supérieur à m, on aboutit aussi à une contradiction. Donc il n’existe pas d’extension de R satisfaisant les axiomes d’incidence, d’ordre de congruence et d’Archimède.

Notes et références

Hilbert 1971, p. 146 commentaire de Bernays.
toujours au chapitre V, Hilbert 1971, p. 124
appelés axiomes d'association par Laugel (Hilbert 1900), d'appartenance par Rossier (Hilbert 1971), qui utilise aussi incidence, et axiomes d'incidences par Artin 1957, Greenberg 1993 et Arsac 1998.
Hilbert 1971, p. 43 (commentaire de Rossier)
L'énoncé de Hilbert, à partir de la 7^e édition, est plus précis : il donne les « propriétés fondamentales », axiomes ou déduites de ceux-ci, qu'il est nécessaire de conserver (Hilbert 1971, p. 41).
à la suite d'une remarque de Paul Bernays, Hilbert 1971, p. 41 et page 43 pour la citation.
Grattan-Guinness 2000, p. 210
Hilbert 1971, p. 281 commentaire de Rossier
Greenberg 1993, p. 98

Bibliographie

Grundlagen der Geometrie

Les Grundlagen der Geometrie ont connu 10 éditions de 1899 à 1968, 7 du vivant de Hilbert, et les 3 dernières préparées par Paul Bernays qui avait été un de ses proches collaborateurs, (source et détails : Hilbert 1971 préface de Rossier p. VI et VII), et d'autres ultérieures.

Éditions

(de) David Hilbert, Grundlagen der geometrie, Leipzig, Teubner, 1899 (comme partie d'un mémoire Festschrift zur Feier der Enthüllung des Gauss-Weber-Denkmals in Göttingen).
(de) David Hilbert, Grundlagen der geometrie, Leipzig, Teubner, 1903, 2^e éd. (lire en ligne)

Traductions

David Hilbert (trad. L. Laugel), Les principes fondamentaux de la géométrie, Paris, Gauthier-Villars, 1900 (lire en ligne) traduction de la première édition avec des additions de Hilbert, reprises par celui-ci dans la seconde édition de 1903.
(en) David Hilbert (trad. E. J. Townsend), The Foundations of Geometry, 1902 (lire en ligne) traduction de la première édition avec prise en compte des additions de Hilbert à la traduction de L. Laugel.
David Hilbert (trad. PauL Rossier), Les fondements de la géométrie, Paris, Dunod, 1971 (réimpr. Gabay 1997), 311 p. (ISBN 2-87647-127-2) Édition critique avec introduction et compléments préparée par Paul Rossier. La traduction est celle de la 10^e édition, avec indications des variantes des éditions successives.

Autres

Gilbert Arsac, L'axiomatique de Hilbert et l'enseignement de la géométrie au Collège et au Lycée, Lyon, Aleas, octobre 1998, 125 p. (ISBN 2-84301-004-7)
M. J. Greenberg, Euclidiean and non-Euclidiean geometries, W.H. Freeman and Company, 1993 (ISBN 0-7167-2446-4)
H. Languereau Les 100 ans de la géométrie de Hilbert, Mathématiques vivantes Bulletin IREM de Besançon n^o 66 2001 archive
Emil Artin, Algèbre géométrique, Calmann-Lévy, traduction de Geometric algebra New York, Interscience Publishers, Inc., 1957, chap.II (présentation axiomatique, essentiellement de la géométrie plane, inspirée de celle de Hilbert et modernisée).
Jacqueline Lelong-Ferrand, Fondements de la géométrie, Paris, PUF, 1985, 287 p. (ISBN 2-13-038851-5).
Yves Martin - IREM de La Réunion Géométrie non arguésienne dynamique sur cultureMATH (Ressources pour les enseignants de mathématiques, site expert des Écoles Normales Supérieures et du Ministère de l'Éducation Nationale) : plan de Moulton et autres.
(en) Ivor Grattan-Guinness, In Search of Mathematical Roots, Princeton University Press, 2000, 690 p. (ISBN 978-0-691-05858-0, présentation en ligne) section 4.7.

Liens externes

Les axiomes de Hilbert par Fabien Besnard, professeur de mathématiques, en lycée et à l'EPF

Portail de la géométrie
Portail de la logique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Hilbert 1971, p. 146 commentaire de Bernays.

[2] toujours au chapitre V, Hilbert 1971, p. 124

[3] és axiomes d'association par Laugel (Hilbert 1900), d'appartenance par Rossier (Hilbert 1971), qui utilise aussi incidence, et axiomes d'incidences par Artin 1957, Greenberg 1993 et Arsac 1998.

[4] Hilbert 1971, p. 43 (commentaire de Rossier)

[5] L'énoncé de Hilbert, à partir de la 7^e édition, est plus précis : il donne les « propriétés fondamentales », axiomes ou déduites de ceux-ci, qu'il est nécessaire de conserver (Hilbert 1971, p. 41).

[6] à la suite d'une remarque de Paul Bernays, Hilbert 1971, p. 41 et page 43 pour la citation.

[igg210-7] Grattan-Guinness 2000, p. 210

[8] Hilbert 1971, p. 281 commentaire de Rossier

[9] Greenberg 1993, p. 98