Interféromètre de Michelson

L'interféromètre de Michelson est constitué de deux miroirs M1 et M2 et d'une lame semi-réfléchissante appelée séparatrice. Ces trois éléments sont orientables et M2 est déplaçable par translation (pour ajuster la distance notée d sur le schéma)

Sur le schéma ci-contre, qui modélise un Michelson utilisé en lame d'air, la source de lumière envoie un rayon (d'intensité I) vers la lame séparatrice. Ce rayon est divisé en deux rayons (bleu et vert) d'intensité I/2. M1' représente l'image du miroir M1 par la séparatrice, donc symétrique par rapport à celle-ci ; le trait pointillé bleu représente donc un trajet virtuel équivalent au trajet réel de la lumière vers le miroir M1. La différence de longueur d des bras de l'interféromètre induit une différence de marche entre les deux rayons égale à 2d.

Dans la configuration en lame d'air, si l'inclinaison du rayon par rapport à la normale de la lame (ici 0°) vaut i, la différence de marche vaut ${\displaystyle 2d\cos i}$ (en l'occurrence ${\displaystyle 2d}$).

Vue de dessus d'un interféromètre de Michelson

Dans la pratique, la lame séparatrice possède une certaine épaisseur. Et la face semi-réfléchissante est la face du côté d'entrée de la lumière. Alors que le rayon vert ne la traverse qu'une fois, le rayon bleu la traverse trois fois. Cette traversée induit une différence de marche supplémentaire.

Pour corriger cela, on place sur le chemin du rayon violet et vert (c’est-à-dire légèrement en haut et à gauche de la séparatrice) une lame dite compensatrice qui doit être de même indice de réfraction et de même épaisseur que la séparatrice, parfaitement parallèle à celle-ci.

Ainsi, le rayon vert et le bleu auront traversé trois fois (ou quatre si le rayon initial traverse lui aussi la compensatrice) une lame de même épaisseur et de même indice de réfraction. Aucune différence supplémentaire n'est donc induite.

Schéma d’un interféromètre de Michelson utilisé en lumière blanche.

Pour configurer l'interféromètre de Michelson en lame d'air, il suffit d'agir sur la distance d représentée sur le schéma, comme cela est indiqué dans la partie précédente. En pratique, cela s'effectue souvent à l'aide d'une vis de chariotage. Nous nous pencherons ici sur les résultats obtenus lors d'une expérimentation avec cette configuration.

La figure d'interférence observable est celle qui est représentée sur le schéma de droite. On peut y observer un ensemble d'anneaux concentriques, successivement sombres et clairs. La figure est constituée d'anneaux d'égale inclinaison.

On explique cette forme des franges à l'aide de l'expression de la différence de marche dans cette configuration : ${\displaystyle \delta =2d\cos i}$ où i correspond à l'angle formé entre la normale au support de visualisation et la droite issue du milieu des deux sources secondaires. Une différence de marche constante (c'est-à-dire un état d’interférence constant) correspond donc à un angle i constant, d'où une figure d’interférence présentant des anneaux.

Cas particulier de l'observation, lors du contact optique, c'est-à-dire lorsque la distance d est réduite à zéro, on observe une figure d'interférence avec un contraste nul. On a donc une teinte unie. Cette mesure peut permettre de tester la planéité des miroirs utilisés.

• 
  Figure d'interférence obtenue avec un interféromètre de Michelson en configuration lame d'air.
• 
  Figure d'interférence obtenue avec un interféromètre de Michelson en configuration lame d'air éclairé par une lampe à vapeur de mercure

Schéma de la formation des anneaux du Michelson en lame d'air, avec lentille.

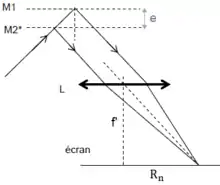
On peut déterminer le rayon théorique des anneaux :

on a ${\displaystyle I=2A^{2}(1+\cos(\phi ))}$ . Donc les franges brillantes correspondent à ${\displaystyle \cos(\phi )=1}$ c'est-à-dire ${\displaystyle \phi =2k\pi }$ ou encore ${\displaystyle \delta =k\lambda }$ , et les franges sombres à ${\displaystyle \cos(\phi )=-1}$ c'est-à-dire ${\displaystyle \phi =(2k+1)\pi }$ ou encore ${\displaystyle \delta ={\frac {\lambda (2k+1)}{2}}}$ .

D'après l'expression de l'ordre d’interférence ${\displaystyle p={\frac {\delta }{\lambda }}={\frac {2e}{\lambda }}(1-{\frac {r^{2}}{2f'^{2}}})}$ (en effectuant un développement limité du cosinus).

On a alors le rayon d'un anneau (caractérisé par son ordre d’interférence p) ${\displaystyle R_{p}=f'{\sqrt {2\left({\frac {2e}{\lambda }}-p\right){\frac {\lambda }{2e}}}}=f'{\sqrt {2\left(1-p{\frac {\lambda }{2e}}\right)}}}$

Figure d'interférence obtenue avec un interféromètre de Michelson en configuration coin d'air éclairé par une lampe blanche.

La configuration en coin d'air consiste à introduire un angle entre les deux miroirs, et donc obtenir un dispositif où M1 et M2 ne sont plus perpendiculaires.

La figure d'interférence, cette fois-ci, est composée de raies toutes parallèles, séparées par une distance (l'interfrange) notée i.

On y voit au milieu entre les deux raies noires l'interférence d'ordre 0, ensuite les teintes de Newton à droite et à gauche, et enfin, pour des ordres d'interférence élevés en valeur absolue, on a le blanc d'ordre supérieur (apparaissant gris dans l'illustration suivante).

Si le Michelson est éclairé par une source (quasi-)ponctuelle, comme par un laser hélium-néon, les interférences sont visibles dans toute la zone de recouvrement des faisceaux : on dit que les interférences ne sont pas localisées. On peut les observer sans aucun système optique sous réserve de vérifier la condition de cohérence temporelle également (par exemple en utilisant un laser).

Si le Michelson, réglé en coin d'air, est éclairé par une source étendue, comme par une lampe spectrale ou bien une lampe blanche, les interférences ne sont pas brouillées mais elles sont localisées au voisinage du coin d'air. On peut les observer :

• soit en formant l'image du coin d'air (c’est-à-dire des miroirs) sur un écran grâce à une lentille convergente;
• soit en observant à l'œil nu le coin d'air (c’est-à-dire les miroirs) en accommodant.

Quand on utilise le Michelson réglé en lame d'air, éclairé par une source étendue, les interférences ne sont pas brouillées mais elles sont localisées à l'infini. On peut les observer :

• soit en plaçant un écran dans le plan focal image d'une lentille convergente;
• soit en observant à l'œil nu sans accommoder.

• Interférométrie
• Spectroscopie à interférence réflectométrique

• Simulations informatiques:
  • TD Info Michelson / Université de Nantes
• L'interféromètre de Michelson et son application à la tomographie (ESPCI ParisTech, École centrale Paris)
• Une vidéo montrant et expliquant les expériences classiques faites avec un interféromètre de Michelson
• Simulation complète des principaux dispositifs d'interférométrie. Université Paris XI

• Portail de la physique
• Portail de l’optique