Loi de Boyle-Mariotte

La loi de Boyle-Mariotte ou loi de Mariotte, souvent appelée loi de Boyle dans le monde anglo-saxon, du nom du physicien et chimiste irlandais Robert Boyle et de l'abbé physicien et botaniste français Edme Mariotte, est l'une des lois de la thermodynamique constituant la loi des gaz parfaits. Elle relie la pression et le volume d'un gaz parfait à température constante.

Dispositif de Kröncke pour la démonstration de la loi Boyle-Mariotte.
Musée des sciences de Milan, ((it) voir sur le site du musée).

Énoncé

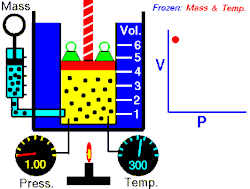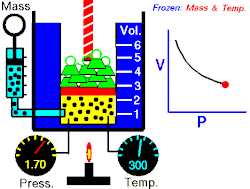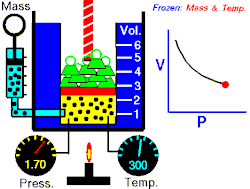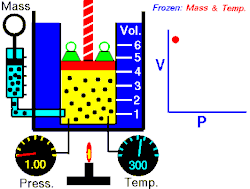
Animation montrant la relation entre pression et volume lorsque la température est maintenue constante.

La loi de Boyle-Mariotte relie la pression et le volume d'un gaz parfait à température constante. On trace ainsi une courbe isotherme du gaz. Boyle et Mariotte ont constaté que la courbe $P=f\!\left(V\right)$ était proche, à quelques pourcents près, d'une branche d'hyperbole équilatère en coordonnées de Clapeyron $\left(P,V\right)$ , soit $PV={\text{constante}}$ pour une température donnée constante.

En d'autres termes, à une température donnée et maintenue constante, une diminution du volume d'un gaz entraîne une augmentation de sa pression. Inversement, la diminution de la pression du gaz se traduit par une augmentation de son volume. La valeur exacte de la constante n'a pas besoin d'être connue pour appliquer la loi entre deux volumes de gaz sous des pressions différentes, à la même température :

Loi de Boyle-Mariotte :

P_{1}\times V_{1}=P_{2}\times V_{2}

La loi a été découverte à quelques années d'intervalle par l'Irlandais Robert Boyle (en 1662) et par le Français Edme Mariotte (en 1676). Le Français Guillaume Amontons précisa en 1702 que cette loi n'est valable qu'à température constante et est plus précise aux basses pressions.

Limitations

Isothermes de l'équation d'état de van der Waals dans un diagramme d'Amagat.
En marron : courbe de Boyle-Mariotte ; en violet : isotherme de Boyle-Mariotte ; en rouge : isotherme critique.
Dans ce type de diagramme, les courbes isothermes d'un gaz parfait sont des droites horizontales en vertu de la loi de Boyle-Mariotte.

Lorsque l'on trace dans un diagramme d'Amagat, à température $T$ et quantité de matière $n$ constantes, le produit $PV$ en fonction de la pression $P$ pour un gaz parfait, on obtient, en vertu de la loi de Boyle-Mariotte, une droite horizontale. En faisant varier la température, on obtient un faisceau de droites parallèles appelées isothermes. Plus la température est élevée, plus l'isotherme est haute dans le diagramme.

Il n'en va pas de même pour les gaz réels, pour lesquels le produit $PV$ , à température $T$ et quantité de matière $n$ constantes, varie en fonction de la pression. La figure ci-contre représente le diagramme d'Amagat d'un gaz répondant à l'équation d'état de van der Waals : cette équation d'état représente qualitativement le phénomène physique réel.

Les isothermes d'un gaz réel dans un diagramme d'Amagat décroissent avec une pression croissante aux basses pressions, puis croissent avec la pression aux hautes pressions. Le point auquel la tangente à l'isotherme est horizontale, soit $\left({\partial PV \over \partial P}\right)_{T,n}=0$ , et auquel la pente de l'isotherme s'inverse, est appelé point de Boyle-Mariotte de l'isotherme. Le lieu géométrique des points de Boyle-Mariotte, qui sont les minimums des isothermes, est appelé courbe de Boyle-Mariotte[1]. Il existe une température appelée température de Boyle-Mariotte au-delà de laquelle les isothermes sont croissantes monotones, l'isotherme correspondante est appelée isotherme de Boyle-Mariotte.

Par contre, lorsque la pression $P$ tend vers zéro, quelle que soit la température $T$ , le comportement d'un gaz réel, quel qu'il soit, tend vers celui du gaz parfait et la valeur de $PV$ du gaz réel tend vers $nRT$ (avec $R$ la constante universelle des gaz parfaits). La loi de Boyle-Mariotte n'est donc applicable qu'aux basses pressions, généralement moins de 10 bar ou 10 atm.

Applications

Loi des gaz parfaits

La loi de Boyle-Mariotte est l'une des composantes de la loi des gaz parfaits :

Loi des gaz parfaits :

PV=nRT

avec :

$P$ la pression ;
$V$ le volume ;
$n$ la quantité de matière (nombre de moles) ;
$R$ la constante universelle des gaz parfaits (8,314 J mol⁻¹ K⁻¹) ;
$T$ la température absolue.

Ainsi pour une quantité de matière $n$ donnée, à une température $T$ donnée, quel que soit le gaz $PV={\text{constante universelle}}$ .

Autonomie d'une bouteille de gaz

Détente du contenu d'une bouteille respiratoire.

La loi de Boyle-Mariotte permet de déterminer l'autonomie d'une source de gaz en fonction du débit de consommation :

Autonomie d'une bouteille :

t={PV \over Q}

avec :

$t$ l'autonomie de la bouteille (en minutes) ;
$P$ la pression relative du gaz contenu dans la bouteille (en bars relatifs) ;
$V$ le volume de la bouteille (en litres) ;
$Q$ la consommation moyenne, soit le débit volumique de gaz après détente (en litres par minute, l/min).

Pour démontrer cette relation, on considère une bouteille de gaz ayant les caractéristiques suivantes :

$P_{1}=P$ la pression dans la bouteille ;
$V_{1}=V$ le volume de la bouteille.

On considère également :

$P_{2}=P_{\text{atm}}$ la pression atmosphérique (environ 101 325 Pa) ;
$V_{2}=V_{\text{atm}}$ le volume produit par la détente du contenu de la bouteille à pression atmosphérique (en considérant la détente à température constante).

L'autonomie $t$ permise par la bouteille est donnée par :

t={V_{\text{atm}} \over Q}

La loi de Boyle-Mariotte donne :

P\times V=P_{\text{atm}}\times V_{\text{atm}}

on a :

t={P \over P_{\text{atm}}}{V \over Q}

En considérant les deux pressions en bars, puisque 1 bar = 100 000 Pa, $P_{\text{atm}}$ ≈ 1 bar, on retrouve la relation donnée plus haut.

Remarque

La pression

P

dans la bouteille est la pression relative et non la pression absolue du gaz, qui est égale à

P^{\prime }=P+P_{\text{atm}}

. En effet, lorsque la pression dans la bouteille atteint la pression atmosphérique la bouteille cesse de se vider et le reliquat de gaz dans la bouteille, égal au volume

V

à

P_{\text{atm}}

, n'est pas utilisable. Considérer la pression absolue dans le calcul précédent fausse donc le calcul de l'autonomie de la bouteille en produisant une valeur surestimée.

Exemple

La loi de Boyle-Mariotte permet par exemple d'estimer l'autonomie permise par les bouteilles de plongée, les ARI utilisés par les pompiers, les mono-bouteilles utilisées en oxygénothérapie.

Pour une bouteille d'ARI portée par un sapeur-pompier ayant un matériel normé et une condition physique normale :

la pression minimale nécessaire pour l'engagement d'une mono-bouteille d'un ARI est de $P$ = 280 bar (pression relative) ;
le volume d'une mono-bouteille $V$ = 6,8 litres ;
la consommation moyenne d'air d'un individu normal lors d'un entrainement $Q$ = 90 l/min.

On a :

t={P\times V \over Q}={280\times 6{,}8 \over 90}

≈ 21,155 minutes.

Voir aussi

Références

Thermodynamique et énergétique, Volume 1, Lucien Borel, Daniel Favrat, Presses Polytechniques et Universitaires Romandes, 2005, (ISBN 2-88074-545-4), p. 264.

Bibliographie

Danielle Baeyens-Volant, Pascal Laurent et Nathalie Warzée, Chimie générale : Exercices et méthodes, Dunod, 2019, 384 p. (ISBN 978-2-10-080272-2, lire en ligne), p. 188.
Michel Lagière, Physique industrielle des fluides : Notions fondamentales et applications numériques, Paris, Éditions Technip, 1996, 394 p. (ISBN 2-7108-0701-7, lire en ligne), p. 122.

Liens externes

Loi de Boyle-Mariotte sur le site Bibliothèque virtuelle Allô Prof.

Articles connexes

Diagramme d'Amagat

Portail de la physique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Thermodynamique et énergétique, Volume 1, Lucien Borel, Daniel Favrat, Presses Polytechniques et Universitaires Romandes, 2005, (ISBN 2-88074-545-4), p. 264.