Loi sécante hyperbolique
En théorie des probabilités et en statistique, la loi sécante hyperbolique est une loi de probabilité à densité dont la densité de probabilité et la fonction caractéristique sont proportionnelles à la fonction sécante hyperbolique.
| Loi sécante hyperbolique | |
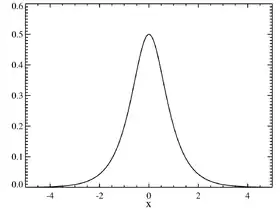 Densité de probabilité | |
 Fonction de répartition | |
| Paramètres | aucun |
|---|---|
| Support | |
| Densité de probabilité | |
| Fonction de répartition | |
| Espérance | |
| Médiane | |
| Mode | |
| Variance | |
| Asymétrie | |
| Kurtosis normalisé | |
| Entropie | 4/π K |
| Fonction génératrice des moments | pour |
| Fonction caractéristique | pour |
Description
La densité de la loi sécante hyperbolique est donnée par la transformation suivante de la fonction sécante hyperbolique :
La fonction de répartition de la loi sécante hyperbolique est :
où arctan est la fonction trigonométrique inverse arc tangente. La fonction quantile, ou fonction inverse de la fonction de répartition, est donnée par :
où arsinh est la fonction inverse sinus hyperbolique et cot est la fonction cotangente.
La loi sécante hyperbolique partage plusieurs propriétés avec la loi normale : elle est symétrique, de variance unitaire et de moyenne, médiane et mode nuls ; Sa densité est proportionnelle à sa fonction caractéristique. Cependant la loi sécante hyperbolique est leptokurtique, c'est-à-dire qu'elle possède un pic autour de sa moyenne et une longue traîne, comparée à celle de la loi normale.
Johnson et al. (1995, p. 147) donnent cette loi dans le contexte d'une classe de lois qui généralisent la loi logistique, ils utilisent cependant une paramétrisation différente de celle présentée ici.
Références
- W. D. Baten, « The probability law for the sum of n independent variables, each subject to the law », Bulletin of the American Mathematical Society, vol. 40, no 4, , p. 284-290 (DOI 10.1090/S0002-9904-1934-05852-X)
- J. Talacko, 1956, "Perks' distributions and their role in the theory of Wiener's stochastic variables", Trabajos de Estadistica 7:159-174.
- Luc Devroye, 1986, Non-Uniform Random Variate Generation, Springer-Verlag, New York. Section IX.7.2.
- G.K. Smyth, « A note on modelling cross correlations: Hyperbolic secant regression », Biometrika, vol. 81, no 2, , p. 396–402 (DOI 10.1093/biomet/81.2.396, lire en ligne)
- Norman L. Johnson, Samuel Kotz and N. Balakrishnan, 1995, Continuous Univariate Distributions, volume 2, (ISBN 0-471-58494-0).