Méthode FORM-SORM

On suppose que les variables aléatoires ont une distribution normale.

Si les variables sont normales d'espérance μ_i et d'écart type σ_i, on les transforme également en variables de loi centrées réduites

U_i = (X_i - μ_i)/σ_i

X_i = σ_iU_i + μ_i

Si les variables aléatoires X_i ne sont pas normales, on les transforme pour avoir des variables U_i suivant lois normales centrées réduites ; cette opération est la « transformation de Nataf et Rosenblatt » :

U_i = Φ^-1(F_i(X_i))

et réciproquement

X_i = F^-1(Φ_i(U_i))

où Φ (lettre grecque Phi) est la fonction de répartition de la loi normale centrée réduite, et F_i la fonction de répartition de X_i.

Plus on est proche du sommet de l'hypersurface y, plus la densité de probabilité est élevée. Les fonctions de densité ƒ_i étant des courbes en cloche symétriques, y forme une « colline » : plus on s'éloigne du sommet, plus la densité de probabilité y diminue. Donc, le point le plus critique, le point de conception x*, est le point de la zone de défaillance F le plus proche du sommet.

La méthode FORM-SORM consiste à trouver le point de la zone frontière g(x₁, …, x_n) = 0 le plus proche du sommet. Dans l'espace centré réduit, le sommet de y se trouve à l'origine, le point de coordonnées (0, 0, …, 0). La fonction de défaillance devient alors g* :

F(t) = α ⇔ g*(u₁, …, u_n) ≥ 0.

La distance à l'origine est donc

${\displaystyle d^{*}={\sqrt {u_{1}^{2}+u_{2}^{2}+\cdots +u_{n}^{2}}}}$

et ainsi,

la méthode consiste à minimiser d*(u₁, …, u_n) avec pour contrainte g*(u₁, …, u_n) = 0.

C'est une méthode d'optimisation quadratique : en effet, minimiser d* revient à minimiser d*² (puisque la fonction carré est strictement croissante sur [0 ; +∞[), on doit donc minimiser une fonction quadratique ∑x_i² avec une contrainte linéaire.

La distance minimale trouvée est appelée indice de fiabilité et est noté β (lettre grecque bêta) :

β = d*(x*).

Distribution de la contrainte S et de la résistance R : toutes les situations (R, S) ont une densité de probabilité (surface en niveaux de gris). La zone où la marge m = R - S est positive est la zone où le système survit (R > S).

Même situation vue de dessus.

Point de conception : maximum de la courbe m = 0.

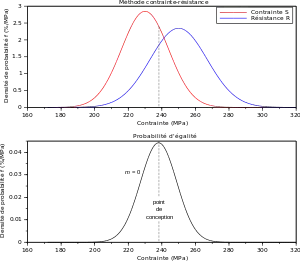
Dans la méthode contrainte-résistance, la condition sur la durée de vie

F(t) ≤ α

s'exprime par une résistance R supérieure à une contrainte S (stress) :

R ≥ S

ou plutôt en définissant la marge m = R - S :

m ≥ 0.

Cette marge m est donc une fonction de défaillance :

g(R, S) = m.

Si l'on dispose des distributions (densités de probabilité) ƒ_R et ƒ_S, on peut alors déterminer cette probabilité :

F(t) = P(R ≤ S) = P(m ≤ 0)

La probabilité d'avoir une couple de valeurs dans un intervalle ([S, S + dS], [R, R+dR]) est donné par

P([S, S + dS]∩[R, R+dR]) = P([S, S + dS])×P([R, R+dR]) = ƒ_S׃_R×dS×dR.

On peut tracer la surface y = ƒ_S׃_R, ainsi que la ligne de séparation m = 0 : cette ligne marque l'état limite entre la situation de survie et la situation de défaillance. Une méthode simple d'estimer la probabilité P(m ≤ 0) consiste à utiliser une méthode de Monte-Carlo : on effectue N tirages aléatoires de couples (R, S), et l'on dénombre les n situations pour lesquelles m ≤ 0 :

P(m ≤ 0) ≃ n/N.

Si l'on veut un risque α faible, cela signifie que le sommet de la surface doit être loin de l'état limite m = 0.

Le point que l'on veut le mieux connaître est le maximum de la courbe m = 0 ; c'est notre « point de conception ». Si le risque α est faible, alors le point de conception est loin du sommet de la surface. Cela signifie que lors du tirage aléatoire, peu de points seront proches du point de conception ; il faudra donc de très nombreux tirages — N devra être très grand — si l'on veut caractériser ce point.

Exemple

Nous avons représenté ci-contre une situation pour laquelle :

• la contrainte S suit une loi normale d'espérance μ_S = 230 MPa et un écart type σ_S = 14 Mpa ;
• la résistance R suit une loi normale d'espérance μ_R = 250 MPa et un écart type σ_R = 17 Mpa.

Graphiquement, on constate que le maximum de l'état limite se trouve à 238 MPa. Ce point est en général proche de l'intersection des courbes ƒ_S et ƒ_R.

Une méthode de Monte-Carlo avec un million de tirages et un intervalle de confiance de 5 %[1] donne 18,1 % ± 0,2 % de défaillance.

N = 1e6 # nombre d'événements (tirs)
alpha = 0.005 # risque

# paramètres des lois
muR = 250
sigmaR = 17
muS = 230
sigmaS = 14

# calculs
R = rnorm(N, muR, sigmaR)
S = rnorm(N, muS, sigmaS) 
Mbool = S>R

moyenne = mean(Mbool)

epsilon = sqrt(log(2/alpha)/(2*(N + 1)))

# affichage des résultats
print(moyenne)
print(epsilon)

N = 1e6; // nombre d'événements (tirs)
alpha = 0.005; // risque

// Paramètres des lois
muR = 250;
sigmaR = 17;
muS = 230;
sigmaS = 14;

// Calculs
R = muR + sigmaR*rand(N, 1, "normal"); // résistance
S = muS + sigmaS*rand(N, 1, "normal"); // contrainte
Mbool = S>R; // comparaison des valeurs (matrice de booléens)
moyenne = sum(Mbool)/N; // les "vrai" comptent pour 1 et les "faux" pour 0
epsilon = sqrt(log(2/alpha)/(2*(N + 1)));

// Affichage des résultats
disp(string(100*moyenne)+" % +/- "+...
    +string(100*epsilon)+" %") // affichage du résultat

Détermination du point de conception par la méthode FORM-SORM.

La méthode FORM est une méthode permettant d'obtenir une valeur approchée de la probabilité de défaillance à partir du point de conception. Elle suppose que les distributions de S et de R sont normales.

La première étape consiste à passer dans l'espace des lois centrées réduites : on transforme les coordonnées pour avoir des probabilités de densité d'espérance nulle et de variance 1. Cette étape est appelée « transformation de Nattaf et Rosenblatt ». Les nouvelles coordonnées sont appelées S* et R* :

${\displaystyle \mathrm {R} ^{*}={\frac {\mathrm {R} -\mu _{\mathrm {R} }}{\sigma _{\mathrm {R} }}}}$ ;

${\displaystyle \mathrm {S} ^{*}={\frac {\mathrm {S} -\mu _{\mathrm {S} }}{\sigma _{\mathrm {S} }}}}$.

Le sommet de la surface ƒ_S*׃_R* se trouve donc aux coordonnées (0 ; 0). La droite d'état limite m = 0 (R - S = 0) devient donc :

${\displaystyle \mathrm {R} -\mathrm {S} =0\Longleftrightarrow \sigma _{\mathrm {R} }\times \mathrm {R} ^{*}+\mu _{\mathrm {R} }-(\sigma _{\mathrm {S} }\times \mathrm {S} ^{*}+\mu _{\mathrm {S} })=0}$

ce que l'on peut noter

m* = 0

avec

m*(R*, S*) = σ_R×R* + μ_R - (σ_S×S* + μ_S).

Le point de conception est le point de densité de probabilité maximale sur la droite m* = 0. Du fait des propriétés de symétrie de la surface ƒ_S*׃_R*, c'est aussi le plus proche de l'origine (0 ; 0) — sommet de la surface —, c'est-à-dire celui pour lequel la quantité

d*² = R*² + S*²

est minimale.

Pour trouver ce point, on part d'un couple (R*, S*) arbitraire, et l'on applique un algorithme d'optimisation (itératif) pour avoir le minimum de d* avec comme contrainte m* = 0.

La distance d* atteinte est alors l'indice de fiabilité β, et la probabilité de défaillance P_f s'obtient avec la fonction de répartition Φ de la loi normale centrée réduite :

P_f = Φ(-β) ;

c'est la méthode FORM.

Notons que la surface obtenue avec la transformation de Nataff et Rosenblatt est toujours la même ; c'est la droite m* = 0 qui change d'un problème à l'autre.

Exemple

La transformation de Nattaf-Rosenblatt est :

${\displaystyle \mathrm {R} ^{*}={\frac {\mathrm {R} -250}{17}}}$ ;

${\displaystyle \mathrm {S} ^{*}={\frac {\mathrm {S} -230}{14}}}$.

On a

m* = 17×R* + 250 - (14×S* + 230) = 17×R* - 14×S* + 20.

L'optimisation nous donne le point de conception suivant :

R* = -0,701 ; S* = 0,577 ; R = S = 238 MPa

β = 0,908 ;

P_f = 0,182 = 18,2 %.

Comme dans notre exemple les lois sont effectivement normales et g* est effectivement linéaire, nous avons un résultat « exact » aux arrondis près : l'approximation provient uniquement du fait que l'on a une résolution numérique.

Les logiciels ont en général deux types de solveurs. Certains utilisent un solveur non-linéaire « généraliste » ; il faut donc leur définir la fonction g, ainsi que la contrainte

h = 0, avec h = σ_R×R* - σ_S×S* + (μ_R - μ_S).

Le solveur cherche à minimiser une fonction qui est la distance à laquelle on ajoute une fonction permettant de prendre en compte la contrainte (par exemple une pénalité qui augmente vers +∞ lorsque l'on s'éloigne des conditions de contrainte). C'est le cas des solveurs des tableurs, et du solveur constrOptim() du langage R.

Mais nous sommes ici en présence d'un problème d'optimisation quadratique, ce qui permet d'utiliser un solveur spécifique (Goldfarb et Idnani) ; c'est le cas de la fonction solve.QP du langage R, et de la fonction qpsolve de Scilab. Le problème s'écrit alors de manière matricielle

${\displaystyle g(\mathbf {x} )={\frac {1}{2}}d^{*\,2}={\frac {1}{2}}{}^{\mathrm {t} }\mathbf {x} \times \mathrm {Q} \times \mathbf {x} +{}^{\mathrm {t} }p\times \mathbf {x} }$

avec

${\displaystyle \mathbf {x} ={\begin{pmatrix}\mathrm {R} ^{*}\\\mathrm {S} ^{*}\end{pmatrix}}{\text{, }}\mathrm {Q} ={\begin{pmatrix}1&0\\0&1\end{pmatrix}}{\text{, }}p={\begin{pmatrix}0\\0\end{pmatrix}}}$

avec une contrainte d'égalité unique :

C×x = b

avec

C = (σ_R ; -σ_S) ; b = (μ_S - μ_R).

Résolution directe

Le problème est ici relativement simple, nous pouvons donc le résoudre « à la main ». Nous évoluons sur une droite m* = 0, soit d'équation

expression littérale		application numérique
${\displaystyle \sigma _{\mathrm {R} }\times \mathrm {R} ^{*}-\sigma _{\mathrm {S} }\times \mathrm {S} ^{*}+(\mu _{\mathrm {R} }-\mu _{\mathrm {S} })}$		17×R* - 14×S* + 20 = 0
${\displaystyle \Leftrightarrow \mathrm {S} ^{*}={\frac {\sigma _{\mathrm {R} }}{\sigma _{\mathrm {S} }}}\mathrm {R} ^{*}+{\frac {\mu _{\mathrm {R} }-\mu _{\mathrm {S} }}{\sigma _{\mathrm {S} }}}}$		⇔ S* = (17/14)×R* + 20/14

On cherche à minimiser d*² = R*² + S*², qui s'écrit

expression littérale		application numérique
${\displaystyle d^{*\,2}=\mathrm {R} ^{*\,2}+\left({\frac {\sigma _{\mathrm {R} }}{\sigma _{\mathrm {S} }}}\mathrm {R} ^{*}+{\frac {\mu _{\mathrm {R} }-\mu _{\mathrm {S} }}{\sigma _{\mathrm {S} }}}\right)^{2}}$		d*2 = R*2 + ((17/14)×R* + 20/14)2

soit

expression littérale		application numérique
${\displaystyle d^{*\,2}=\left(1+{\frac {\sigma _{\mathrm {R} }^{2}}{\sigma _{\mathrm {S} }^{2}}}\right)\mathrm {R} ^{*\,2}+{\frac {2\sigma _{\mathrm {R} }(\mu _{\mathrm {R} }-\mu _{\mathrm {S} })}{\sigma _{\mathrm {S} }^{2}}}\mathrm {R} ^{*}+{\frac {(\mu _{\mathrm {R} }-\mu _{\mathrm {S} })^{2}}{\sigma _{\mathrm {S} }^{2}}}}$		d*2 ≃ 2,474×R*2 + 3,469×R* + 2,041

Le minimum est là où la dérivée s'annule : (d*²)' = 0 ⇔

expression littérale		application numérique
${\displaystyle 2\left(1+{\frac {\sigma _{\mathrm {R} }^{2}}{\sigma _{\mathrm {S} }^{2}}}\right)\mathrm {R} ^{*}+{\frac {2\sigma _{\mathrm {R} }(\mu _{\mathrm {R} }-\mu _{\mathrm {S} })}{\sigma _{\mathrm {S} }^{2}}}=0}$		4,948×R* + 3,469 = 0
${\displaystyle \Leftrightarrow \mathrm {R} ^{*}=-{\frac {\sigma _{\mathrm {R} }(\mu _{\mathrm {R} }-\mu _{\mathrm {S} })}{\sigma _{\mathrm {S} }^{2}+\sigma _{\mathrm {R} }^{2}}}}$		⇔ R* = -0,7010

et donc

expression littérale		application numérique
${\displaystyle d^{*}={\frac {\mu _{\mathrm {R} }-\mu _{\mathrm {S} }}{\sqrt {\sigma _{\mathrm {S} }^{2}+\sigma _{\mathrm {R} }^{2}}}}}$		d* = 0,908

La table de valeurs de la fonction de répartition de la loi normale donne

Φ(-0,908) = 1 - Φ(0,908) ≃ 1 - Φ(0,91) = 1 - 0,81859 ≃ 0,181.

 

Résolution avec LibreOffice Calc

Interface du solveur de LibreOffice Calc 3.

Le tableur libre LibreOffice Calc dispose d'un solveur.

On construit le tableau suivant :

	A	B	C	D
1	muR	250	sigmaR	17
2	muS	230	sigmaS	14
3
4	R	250
5	S	230
6	R*	=(B4 - B1)/D1
7	S*	=(B5 - B2)/D2
8	d*²	= B6^2 + B7^2
9	m	= B4 - B5

Puis on va dans le menu Outil > Solveur, et dans la boîte de dialogue Solveur qui apparaît, on met :

• Cellule cible : B8
• Optimiser le résultat à : minimum
• Par modification de cellules : B4:B5
• Conditions de limitation :
  • Référence de cellule : B9
  • Opérateur : =
  • Valeur : 0

 

# paramètres de la loi
muR <- 250
sigmaR <- 17
muS <- 230
sigmaS <- 14

# point de départ (R, S) de l'optimisation
theta <- rbind(0, 2)

# fonction à optimiser
detoile2 <- function(x) { # carré de la distance à l'origine, d*²
  Retoile <- x[1]
  Setoile <- x[2]
  Retoile^2 + Setoile^2
  # aperm(x) %*% x
}

# contrainte linéaire
u1 <- c(-sigmaR, sigmaS) 
c1 <- muR - muS

# calcul
a <- constrOptim(theta, detoile2, NULL, u1, c1, mu=1e-3) # optimisation

x <- a$par # (R*, S*)
R <- x[1]*sigmaR + muR
#S <- x[2]*sigmaS + muS
detoile <- sqrt(a$value)
Pf <- pnorm(-detoile)

# affichage des résultats
print(paste("R* = ", x[1], " ; S* = ", x[2]))
print(paste("R = S = ", R))
print(paste("beta = ", detoile))
print(paste("Pf = ", Pf))

#install.packages("quadprog")
library("quadprog")

# paramètres de la loi
muR <- 250
sigmaR <- 17
muS <- 230
sigmaS <- 14

# Optimisation
Dmat <- rbind(c(1, 0), c(0, 1))
dvec <- c(0, 0)
Cmat <- cbind(c(-sigmaR, sigmaS))
bvec <- c(muR - muS)
a <- solve.QP(Dmat, dvec, Cmat, bvec)

x <- a$solution # (R*, S*)
R <- x[1]*sigmaR + muR
#S <- x[2]*sigmaS + muS
detoile <- sqrt(2*a$value)
Pf <- pnorm(-detoile)

# affichage des résultats
print(paste("R* = ", x[1], " ; S* = ", x[2]))
print(paste("R = S = ", R))
print(paste("beta = ", detoile))
print(paste("Pf = ", Pf))

// Données

muR = 250;
sigmaR = 17;
muS = 230;
sigmaS = 14;

// Optimisation

Q = [1, 0 ; 0, 1];
p = [0 ; 0];
C = [sigmaR, -sigmaS];
b = muS - muR;
ci = [];
cs = [];
me = 1;

[x] = qpsolve(Q, p, C, b, ci, cs, me); // Solveur

// Exploitation des données

R = x(1)*sigmaR + muR;
d = norm(x);
Pf = cdfnor("PQ", -d, 0, 1); // fonction Phi

// Affichage

disp("R* = "+string(x(1))+" ; S* = "+string(x(2)));
disp("R = S = "+string(R));
disp("beta = "+string(d));
disp("Pf = "+string(Pf));

• (en) Shankar Sankararaman et Kai Goebel, « Uncertainty Quantification in Remaining Useful Life of Aerospace Components using State Space Models and Inverse FORM », IEEE Aerospace Conference, IEEE,‎ mai 2013 (lire en ligne)
• (en) L. Cizelj, B. Mavko et H. Riesch-Oppermann, « Application of first and second order reliability methods in the safety assessment of cracked steam generator tubing », Nuclear Engineering and Design, Elsevier, n^o 147,‎ 1994 (lire en ligne)

• Portail des probabilités et de la statistique