Loi de fiabilité

Une entreprise met sur le marché N systèmes à l'instant 0 ; nous supposons que ces systèmes ne sont soumis à aucune réparation. On enregistre les moments de première panne t_i : {t₁, t₂…, t_n} que nous supposons classés par ordre croissant. L'indice i est appelé « rang », puisque c'est l'indice d'une suite. Le terme « moment » peut désigner une durée de fonctionnement — en général exprimée heures, jours ou années —, mais aussi un nombre de tours pour une machine tournante, un nombre de cycle pour un système fonctionnant par cycles…

À chaque instant t, on peut déterminer la proportion de systèmes ayant connu une défaillance : c'est la « mortalité », notée F :

${\displaystyle \mathrm {F} (t)={\frac {\mathrm {card} \{t_{j}\leqslant t\}}{\mathrm {N} }}}$

ou, de manière indicée, puisque les t_i sont classés par ordre croissant

${\displaystyle \mathrm {F} _{i}={\frac {i}{\mathrm {N} }}}$, où N est la taille de l'échantillon observé.

La quantité i = card{t_j ≤ t} — nombre de systèmes ayant connu une défaillance avant t (voir Cardinal (mathématiques)) — est appelée « nombre de défaillances cumulé » ; F est aussi appelé « fréquence cumulée ». La mortalité F part de 0 — on considère que tous les systèmes sont en fonctionnement à la mise en service — et atteint 1 (ou 100 %) au bout d'un certain temps — les systèmes ne sont pas éternels et finissent tous par défaillir un jour. Cette fonction F correspond statistiquement à une fonction de répartition.

On définit également la fonction complémentaire, appelée « fiabilité » ou « survie », et notée R (reliability) :

R(t) = 1 - F(t)

R_i = 1 - F_i

C'est en général cette fonction R que l'on considère : elle permet une présentation plus positive de la fiabilité (on parle de ce qui marche plutôt que de ce qui ne marche pas). D'un point de vue mathématiques, F est plus pertinente puisque c'est une fonction de répartition. Dans l'analyse des systèmes complexes, R est plus pertinent dans le cas des associations série, et F est plus pertinent dans le cas des associations parallèles (redondances), voir Schémas fonctionnels de fiabilité. Dans le cas d'un système suivant une loi exponentielle ou de Weibull — des situations très fréquentes —, l'expression de la loi de survie R est plus simple que celle de la loi de mortalité F.

Les instants de survenue des défaillances t_i sont des variables aléatoires. De fait, R (et F) sont également des variables aléatoires, il faut donc corriger les fréquences cumulées, par des formules issues de la loi binomiale.

Définition des fréquences cumulée

Taille de l'échantillon	Formule	Fréquence cumulée
N ≤ 20	formule des rangs médians	${\displaystyle \mathrm {F} _{i}={\frac {i-0,3}{\mathrm {N} +0,4}}}$
20 ≤ N ≤ 50	formule des rangs moyens	${\displaystyle \mathrm {F} _{i}={\frac {i}{\mathrm {N} +1}}}$
N ≥ 50	formule des modes	${\displaystyle \mathrm {F} _{i}={\frac {i}{\mathrm {N} }}}$

On peut par ailleurs définir un intervalle de confiance, pour un risque α bilatéral donné (niveau de confiance bilatéral 1 - α), avec la loi de Fisher, Q_p(ν₁, ν₂) étant le quantile d'ordre p de la loi de Fisher :

limite inférieure : ${\displaystyle \mathrm {F} _{i,\alpha /2}={\frac {i}{i+(\mathrm {N} -i+1)\mathrm {Q} _{1-\alpha /2}(\nu _{1},\nu _{2})}}}$, avec

• ν₁ = 2(N - i + 1)
• ν₂ = 2i

limite supérieure : ${\displaystyle \mathrm {F} _{i,1-\alpha /2}={\frac {(i+1)\mathrm {Q} _{1-\alpha /2}(\nu _{1},\nu _{2})}{\mathrm {N} -i+(i+1)\mathrm {Q} _{1-\alpha /2}(\nu _{1},\nu _{2})}}}$, avec

• ν₁ = 2(i + 1)
• ν₂ = 2(N - i)

On ne connaît pas toujours l'instant de survenue exacte d'une défaillance ; on a parfois le nombre de défaillances survenue durant un intervalle de temps (censure par intervalle). Par exemple, si un système est suivi pendant plusieurs années, on enregistre le nombre de défaillances chaque mois. Ainsi, à l'instant t_i, on a le nombre n_j de défaillances survenues dans les intervalles ]t_{j - 1} ; t_j]. On a alors

${\displaystyle \mathrm {F} _{i}={\frac {\sum _{j=1}^{i}n_{j}}{\mathrm {N} }}}$

éventuellement corrigé par une formule des rangs.

La méthode présentée ci-dessus convient également lorsque l'on arrête l'observation à un moment donné, alors que certains systèmes sont encore en service : c'est un cas de censure à droite, mais pour lequel on n'a aucune donnée après la date de censure.

Par contre, cette méthode ne convient pas lorsque l'on a des censures à gauche ou bien des censures à droite mais avec des dates de défaillance ultérieures ; par exemple, si un système est arrêté ou bien subit une maintenance avant défaillance pour une raison quelconque. Dans ces cas-là, on utilise des méthodes qui calculent une probabilité P_i de défaillance sur un intervalle i, puis en déduisent une fiabilité R_i.

On utilise principalement la méthode de Kaplan-Meier, la méthode actuarielle et la méthode de Turnbull, et plus rarement la méthode de Wayne-Nelson et la méthode du rang corrigé de Herd-Johnson. Si l'on n'a pas de censure, on retrouve en général la formule des rangs moyens ou bien des modes.

On définit la densité de défaillance comme le taux de variation de la fonction de mortalité F. C'est la « vitesse de mortalité » :

${\displaystyle f(t)={\frac {\mathrm {F} (t+\Delta t)-\mathrm {F} (t)}{\Delta t}}={\frac {\Delta \mathrm {F} }{\Delta t}}}$

ou encore :

${\displaystyle f(t)=-{\frac {\mathrm {R} (t+\Delta t)-\mathrm {R} (t)}{\Delta t}}=-{\frac {\Delta \mathrm {R} }{\Delta t}}}$

Si n(t) est le nombre de défaillances cumulées à l'instant t (nombre de défaillances entre 0 et t), on a alors

${\displaystyle \mathrm {F} (t)={\frac {n(t)}{\mathrm {N} }}}$

et donc

${\displaystyle f(t)={\frac {n(t+\Delta t)-n(t)}{\mathrm {N} \Delta t}}={\frac {\Delta n(t)}{\mathrm {N} \Delta t}}}$.

Avec la notation indicée, on a :

${\displaystyle f_{i}={\frac {\mathrm {F} _{i+1}-\mathrm {F} _{i}}{(t_{i+1}-t_{i})}}=-{\frac {\mathrm {R} _{i+1}-\mathrm {R} _{i}}{(t_{i+1}-t_{i})}}={\frac {n_{i+1}}{\mathrm {N} (t_{i+1}-t_{i})}}}$.

Notez bien la différence entre n_i, qui est le nombre de défaillances entre t_i et t_{i + 1}, et n(t) qui est le nombre de défaillances entre 0 et t.

On définit le taux de défaillance λ (lettre grecque lambda) sur un intervalle ]t, t + Δt] comme étant l'opposé du taux de variation relatif de la survie :

${\displaystyle \lambda (t)=-{\frac {1}{\mathrm {R} (t)}}\cdot {\frac {\mathrm {R} (t+\Delta t)-\mathrm {R} (t)}{\Delta t}}={\frac {f(t)}{\mathrm {R} (t)}}}$

C'est donc le rapport entre le nombre de défaillances dans cet intervalle sur le nombre de systèmes restants au début de l'intervalle, divisé par la durée de l'intervalle. C'est un nombre positif. On a :

${\displaystyle \lambda (t)={\frac {n(t+\Delta t)-n(t)}{(\mathrm {N} -n(t))\Delta t}}={\frac {\Delta n(t)}{(\mathrm {N} -n(t))\Delta t}}}$

ou, de manière indicée

${\displaystyle \lambda _{i}={\frac {f_{i}}{\mathrm {R} _{i}}}=-{\frac {1}{\mathrm {R} _{i}}}\cdot {\frac {\mathrm {R} _{i+1}-\mathrm {R} _{i}}{t_{i+1}-t_{i}}}={\frac {n_{i+1}}{(\mathrm {N} -\sum _{j=1}^{i}n_{i})(t_{i+1}-t_{i})}}}$

Pour une population de N systèmes

• R(t) est la proportion de systèmes encore en service à l'instant t. C'est la proportion de systèmes dont la durée de vie T est supérieure à t.

  N·R(t) est le nombre de tels systèmes.

• F(t) est la proportion de systèmes ayant connu une défaillance avant l'instant t. C'est la proportion de systèmes dont la durée de vie T est inférieure ou égale à t.

  N·F(t) est le nombre de tels systèmes.

• ƒ(t)·Δt est la proportion de systèmes qui connaîtront une défaillance dans l'intervalle ]t ; t + Δt]. C'est la proportion de systèmes dont la durée de vie T est dans ]t ; t + Δt].

  N·ƒ(t).Δt est le nombre de tels systèmes.

• λ(t)·Δt est la proportion qui connaîtront une défaillance dans l'intervalle ]t ; t + Δt] parmi les systèmes encore en service à l'instant t. C'est la proportion, parmi les systèmes ayant une durée de vie supérieure à t, des systèmes dont la durée de vie T est dans ]t ; t + Δt].

  N·R(t)·λ(t)·Δt est le nombre de tels systèmes.

Pour un système donné

• R(t) est la probabilité d'être encore en service à l'instant t. C'est la probabilité d'avoir une durée de vie T supérieure à t

  R(t) = P(T > t).

• F(t) est la probabilité d'avoir eu une défaillance avant l'instant t. C'est la probabilité d'avoir une durée de vie T inférieure ou égale à t :

  F(t) = P(T ≤ t).

• ƒ(t)·Δt est la probabilité d'avoir une défaillance dans l'intervalle ]t ; t + Δt]. C'est la probabilité d'avoir une durée de vie T dans ]t ; t + Δt]

  ƒ(t)·Δt = P(T ∈ ]t ; t + Δt]).

• λ(t)·Δt est la probabilité, si le système est encore en service à l'instant t, de connaître une défaillance dans l'intervalle ]t ; t + Δt] (probabilité conditionnelle). C'est la probabilité, si le système a une durée de vie supérieure à t, d'avoir une durée de vie T est dans ]t ; t + Δt].

  λ(t)·Δt = P(T ∈ ]t ; t + Δt] | T > t).

La différence entre la densité ƒ et le taux λ peut être difficile à appréhender. Disons qu'au moment où l'on met un système en service, on sait qu'après une durée d'utilisation t dans le futur, il aura une probabilité ƒ de tomber en panne[1]. Si maintenant on considère un système ayant déjà été utilisé pendant une durée t, on sait qu'il a une probabilité λ de défaillir maintenant[2].

Le point critique est en général la collecte des données.

Le cas le plus simple est celui d'un industriel suivant son parc de machines : il demande à son équipe de maintenance d'enregistrer les défaillances. Dans le cas d'un fabricant qui voudrait évaluer les produits vendus, le problème est plus délicat. Les constructeurs automobiles imposent en général que la maintenance soit faite dans un garage de leur réseau sous peine d'annulation de la garantie, ce qui permet d'obtenir les statistiques pendant cette durée ; le problème est alors que l'on ne sait pas de quelle manière le produit a été utilisé (conduite souple ou nerveuse, autoroute ou ville), on ne connaît que la date de mise en service et le kilométrage.

Mais un fabricant peut aussi vouloir évaluer la loi de survie avant la mise sur le marché, pour pouvoir dimensionner la durée de garantie et conseiller une date de maintenance/révision. Pour cela, il peut effectuer des essais de fiabilité. L'essai doit reproduire l'utilisation réelle du produit, ce qui implique de définir un « profil de mission », c'est-à-dire un mode d'utilisation de référence (type de conduite pour un véhicule, cadence de production et réglages pour une machine industrielle, …).

Un point important consiste, lorsque c'est possible, de distinguer les différents modes de défaillance. En effet, chaque mode de défaillance suit sa propre statistique de mortalité/survie, et l'on peut voir le comportement d'un système complexe comme la composition de chacun des modes. Selon le niveau de détail visé, on peut séparer les données pour chaque organe (sous-système), ou pour un sous-système donné, les différents mode de défaillance — par exemple, pour une pièce mécanique, distinguer l'usure de la rupture en fatigue.

Exemple d'étude de fiabilité (défaillance de locotracteurs) : tracé des fonctions de mortalité F, de survie R et du taux de défaillance λ

Courbe de mortalité et de survie (fiabilité) avec intervalles de confiance (risque α bilatéral de 10 %).

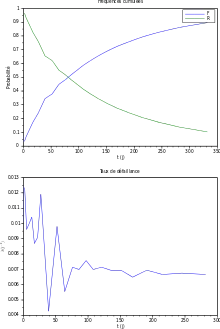
Une entreprise de chemins de fer qui suit l'instant de première panne d'un échantillon de 28 locotracteurs durant un an, date à laquelle a lieu leur première révision. Les durée de service avant la première panne sont donnés en jour et sont, par ordre croissant : {2, 5, 9, 13, 17, 22, 27, 39, 39, 39, 52, 64, 64, 76, 86, 97, 108, 121, 135, 151, 169, 191, 215, 245, 282, 332, > 365, > 365}. On a N = 28, on utilise donc la formule des rangs moyens.

On remarque que deux des locotracteurs n'ont pas subi de défaillance avant leur première révision ; c'est un cas de censure à droite. Ces deux cas ne permettent pas de « placer des points » sur la courbe, mais entrent néanmoins dans la statistique, puisqu'il font partie de l'effectif total N. On utilise dans un premier temps la méthode des rangs.

Défaillance de locotracteurs : courbe de survie (fiabilité) R obtenue par la méthode de Kaplan-Meier.

Reprenons l'exemple avec la méthode de Kaplan-Meier.

Pour chaque date de défaillance t_i, nous déterminons :

• le nombre N_i de systèmes encore en fonctionnement avant t_i (ni défaillants, ni censurés) ;
• le nombre D_i de systèmes défaillant durant la journée t_i ;

et l'on en déduit P_i la probabilité conditionnelle de défaillance durant la journée t_i :

P_i = D_i/N_i

et la fiabilité R_i à l'instant t_i :

${\displaystyle \mathrm {R} _{i}=\prod _{j=1}^{i}(1-\mathrm {P} _{j})}$.

Les censures sont donc prises en compte par les N_i.

Défaillance de locotracteurs : construction de la courbe de survie par la méthode actuarielle.

La méthode actuarielle, elle, consiste à découper la période de surveillance en tronçons d'égale durée. Par rapport à la méthode de Kaplan-Meier, on peut donc avoir des censures au cours d'un tronçon. Lorsqu'on se réfère à une date t_i, on dénombre les défaillances D_i et les censures C_i sur l'intervalle précédant t_i, c'est-à-dire [t_{i - 1} ; t_i[. On a donc

${\displaystyle \mathrm {P} _{i}={\frac {\mathrm {D} _{i}}{\mathrm {N} _{i}-\mathrm {C} _{i}/2}}}$

et toujours

${\displaystyle \mathrm {R} _{i}=\prod _{j=1}^{i}(1-\mathrm {P} _{j})}$.

On considère arbitrairement que sur les C_i systèmes censurés, la moitié aurait présenté une défaillance.

Elle demande moins de calculs que la méthode de Kaplan-Meier, mais en revanche n'utilise pas toute l'information (elle cumule les dates sur une période) et n'est donc précise que pour les grands échantillons. Elle ne s'applique que lorsque l'on a un grand nombre de données, typiquement au moins 30 ou 50 — ce n'est pas le cas de notre exemple, mais nous allons tout de même l'utiliser. Le nombre de classes — le nombre d'intervalles de temps — est typiquement la racine carrée de la taille de l'échantillon. Ici, nous choisissons arbitrairement une durée de deux semaines (quatorze jours).

D'un point de vue phénoménologique, le taux de défaillance instantané λ nous renseigne sur le comportement du système :

• un λ décroissant indique que le taux de panne diminue avec le temps ; on désigne cela par la « mortalité infantile » ou « juvénile » ; c'est typiquement la défaillance de systèmes ayant des « défauts de jeunesse » ou des non-qualités, ou bien des systèmes en rodage ;
• un λ constant indique un système « sans mémoire » : le taux de défaillance est constant, la probabilité de défaillance d'un système donné est uniforme dans le temps, il n'y a pas d'usure ; on parle parfois de panne « purement aléatoire » ;
• un λ croissant : le taux de défaillance augmente avec le temps, indiquant un phénomène de vieillissement, d'usure.

Notons que dans tous les cas, R est décroissant, même si le taux de défaillance décroît.

Nous représentons ci-dessous des courbes pour les trois cas, avec à chaque fois quatre graphiques :

• en haut à gauche, les courbes de survie et de mortalité ;
• en bas à gauche, la fonction de densité de la loi de fiabilité (probabilité de défaillance instantanée) ;
• en haut à droite, le taux de défaillance instantané λ en fonction du temps ;
• en bas à droite, la courbe de survie dans un graphique de Weibull, ln(-ln(R)) en fonction de ln(t), voir Loi de Weibull > Détermination des paramètres de la loi.

• 
  λ décroissant
• 
  λ constant
• 
  λ croissant

Pour revenir sur la différence entre la densité ƒ et le taux λ :

• on voit que quand λ est uniformément décroissant ou constant, ƒ est décroissant ;
• quand λ est uniformément croissant, ƒ présente un pic, les systèmes ont donc tendance à tous tomber en panne en même temps.

Courbes de fiabilité pour un taux de défaillance instantané λ en baignoire.

Dans le cas des systèmes électroniques, on a souvent une courbe de taux de défaillance λ en trois parties (courbe en haut à droite dans la figure ci-contre) : λ décroissant (défaillance des systèmes défectueux), puis λ constant (défaillance aléatoire, la majeure partie de la courbe), puis λ croissant (vieillissement sur la fin). On parle de courbe en « baignoire » (bathtube shaped curve).

Courbes de fiabilité pour un système mécanique : taux de défaillance instantané λ en parabole.

Dans le cas des systèmes mécaniques, on a une courbe de taux de défaillance λ en deux parties : λ décroissants (rodage) puis λ croissants (usure), donnant une courbe globalement parabolique.

Notons que si l'on tourne la courbe de survie d'un quart de tour vers la gauche, on obtient une pyramide des âges exprimée en proportion de la population totale.

• Analyse de survie
• Méthode FORM-SORM