Modulation de largeur d'impulsion
La modulation de largeur d'impulsions (MLI ; en anglais : Pulse Width Modulation, soit PWM), est une technique couramment utilisée pour synthétiser des signaux pseudo analogiques à l'aide de circuits numériques (tout ou rien, 1 ou 0), ou plus généralement à états discrets.
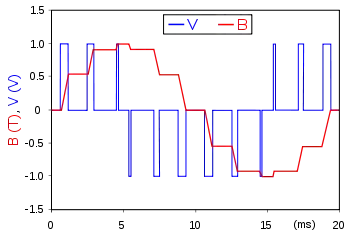
Elle sert à générer un signal pseudo analogique à partir d'un environnement numérique ou analogique pour permettre un traitement de ce signal par des composants en commutation (se comportant comme des interrupteurs ouverts ou fermés).
Le principe général est qu'en appliquant une succession rapide d'états discrets avec des ratio de durée bien choisis, on peut obtenir en ne regardant que la valeur moyenne du signal n'importe quelle valeur intermédiaire [1]
Applications
Les usages les plus fréquents :
- La conversion numérique-analogique
- Les amplificateurs de classe D
- Les alimentations à découpage
- Les variateurs de vitesse
- Les onduleurs
- Les redresseurs
- Plus généralement tous les dispositifs d'électronique de puissance utilisant des composants en commutation à base de semi-conducteurs de type MOSFET, IGBT, GTO. En effet, fondamentalement, les cellules de commutation n'ont que deux états possibles, l'état haut ou l'état bas. Cette structure intrinsèque rend naturelle l'utilisation de PWM pour leur commande.
Il est aussi possible de faire de la transmission de données par cette méthode.
La MLI numérique
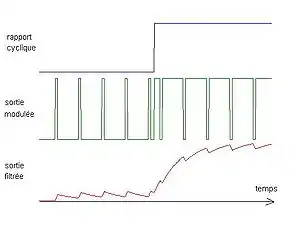
Le principe est de créer un signal logique (valant 0 ou 1), à fréquence fixe mais dont le rapport cyclique est contrôlé numériquement, la valeur moyenne de ce signal étant une grandeur analogique, égale au produit du rapport cyclique par l'amplitude maximale du signal.
Principe de réalisation
Généralement on réalise ce type de fonction à l'aide d'un microcontrôleur. Les microcontrôleurs modernes (ARM Cortex M, PIC, etc.) disposent tous de périphériques dédiées à la génération de PWM. Pour les microcontrôleurs plus anciens (8051, 68HC11), il est possible de détourner le fonctionnement d'un TIMER pour le transformer en générateur de PWM. Enfin en cas d'utilisation d'un microprocesseur, la PWM est généralement émulée.
Dans tous les cas, le principe du périphérique ou du programme d'émulation consiste à générer un signal périodique à assez haute fréquence (généralement supérieure à 20KHz pour éviter d'être dans la gamme audible, bien que cela ne soit pas obligatoire) appelé généralement porteuse (mais l'appellation est impropre) et à générer des impulsions à 1, dont le rapport entre la durée et la période, est égal à la valeur moyenne souhaitée par rapport à la valeur maximum du signal :
où Ton est la durée de l'impulsion, T la période du signal, N la valeur du signal à l'instant t (analogique ou numérique) et Nmax la valeur maximum que peut prendre N.
Dès lors la tension moyenne générée par le signal de PWM (variant entre E et 0) devient :
=
Limites du modèle
Dans le cas de l'utilisation des PWMs pour la conversion de puissance, pour qu'une commande de PWM puisse être utilisé, il faut impérativement que la charge se comporte comme un filtre passe-bas capable de couper la composante haute fréquence tout en conservant la composante variable du signal. La période doit donc être petite (ou la fréquence grande) devant la fréquence de coupure du filtre pour que le signal de PWM n'influence pas la valeur moyenne.
La PWM produit un spectre de fréquence qui peut s'apparenter à celui d'une modulation d'amplitude (d'où l'utilisation abusive du terme de porteuse). Toutefois le signal est plus proche de celui produit par un échantillonnage (avec les problèmes de repliement de spectre que cela peut présenter).
La PWM induit des distorsions importantes du signal modulé ; elles sont comparables à celles dues à un échantillonnage par un signal dont la période est celle de la PWM.
La fréquence de la porteuse peut, en théorie être augmentée indéfiniment, cela peut aussi sembler avantageux étant donné que l'effet principal va être de décaler les harmoniques indésirables en haute fréquence et ainsi diminuer les ondulations de courant. Ce qui va nous limiter en pratique ce sont:
- Les capacités du microcontrôleur à aller au delà d'une certaine fréquence (généralement 1 MHz)
- Le délai minimal nécessaire pour réaliser la commutation des interrupteurs, en effet si un pic de commande est plus court que le temps de réponse du système, les interrupteurs n'auront pas le temps de commuter.
- Dans le cas de l'électronique de puissance, les pertes sont très importantes aux fréquences élevées (pertes par commutation et pertes par conduction). Le MLI peut donc être déconseillé à très haute fréquence.
- Toujours dans le cadre de l'électronique de puissance, il ne faut pas négliger la compatibilité électromagnétique (CEM), qui peut poser problème à l'électronique autour des dispositifs de puissance.
Autres types de MLI
MLI « intersective » ou MLI analogique
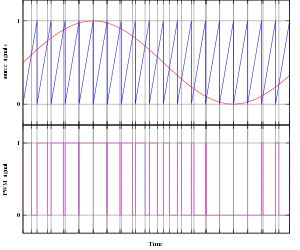
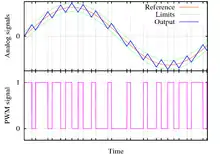
C'est la plus classique. Elle consiste à comparer la modulante (le signal à synthétiser) à une porteuse généralement triangulaire. Le signal de sortie vaut 1 si la modulante est plus grande que la porteuse, 0 sinon ; le signal de sortie change donc d'état à chaque intersection de la modulante et de la porteuse.
Cette méthode se prête bien à une réalisation analogique : il suffit d'un générateur triangle et d'un comparateur. Il existe de nombreux circuits intégrés dédiés.
On peut classifier les sous-types de plusieurs manières :
- Analogique ou numérique échantillonné, selon que la modulante et le comparateur sont en temps continu ou discret ;
- À porteuse triangulaire centrée ou en dents de scie (à gauche ou à droite) ;
- Asynchrone ou synchrone, selon que la modulante et la porteuse sont de fréquence exactement multiples ou non. Nous apportons une attention particulière au lecteur à ne pas confondre le synchronisme des PWM et des moteurs synchrones ou asynchrones. En effet bien qu'ils aient le même nom, leurs définitions sont pour le moins très différentes.
MLI Par injection d'harmoniques d'ordre 3
La technique ci après est utile pour la commande des onduleurs de tension, notamment car il s'agit, entre autres, de réaliser une tension sinusoïdale en sortie du dit convertisseur. Les MLI par injection d'harmoniques d'ordre 3 (Third Harmonic Injection PWM en anglais), sont des variantes simples mais efficaces de la PWM classique (nommée SPWM pour sinusoïdal PWM) décrite précédemment. Leur acronyme dans la littérature se nomme THIPWM dont les deux principalement utilisées que sont la THIPWM1/6 et la THIPWM1/4. Historiquement, c'est la THIPWM1/6 qui a été décrite pour la première fois par Buja en 1975 [2] et ce, afin d'augmenter la zone de linéarité de l'indice de modulation (comme pour la SVM), mais aussi d'augmenter la qualité harmonique des solutions. En effet l'indice de modulation étant classiquement (avec la SPWM) compris entre 0 et 1. l'indice de modulation se voit ici augmenter de 15% grâce à THIPWM1/6 et de 12%grâce à THIPWM1/4. Cette seconde méthode bien qu'ayant une zone de linéarité moins étendue possède l'avantage de réduire le taux de distorsion harmonique par rapport à la variante 1/6.
La réalisation technique de cette méthode est particulièrement simple, il suffit d'ajouter ou au vecteur des tensions modulantes ( étant le pourcentage d'utilisation du bus continu ). Il n'y a rien à changer concernant la porteuse, et cette injection permet d'obtenir des tensions réalisées de meilleure qualité.
La démonstration expliquant l'origine des 15% d'indice de modulation supplémentaire ainsi que l'origine du facteur 1/6 est proposée ci-dessous.[3]
Premièrement, l'idée est d'ajouter un signal périodique de fréquence triple par rapport à la fréquence fondamentale (soit ). Ainsi, on peut écrire la modulante comme étant la somme du signal de référence pondéré () et du signal d'harmonique de rang 3 d'amplitude . Ainsi, la modulante normalisée (en posant ) s'écrit:
Afin de trouver les extremas de cette fonction il est nécessaire de la dériver et de chercher les points pour lesquelles la modulante s'annule:
Ce qui nous donne:
Ainsi les extremas sont atteints lorsque:
(et donc de manière équivalente )
ou
Ainsi, dans ce deuxième cas est égal à:
Or, en remarquant que , on obtient pour la modulante l'équation suivante:
Dans la suite, on peut calculer l'amplitude de la modulante (notée).
Alors, en fonction de la solution considérée, peut prendre les valeurs suivantes:
Ou
Les valeurs optimales de sont alors obtenues en cherchant à minimiser l'amplitude la modulante et donc . En effet cette minimisation permet d'aller chercher l'indice de modulation maximal. Pour calculer cette minimisation on fait encore une fois appel aux dérivées:
Ainsi, il n'y a que trois valeurs possibles pour l'amplitude de la modulante, (-1;-1/3 et 1/6). Il faut choisir celui qui minimise l'amplitude de la modulante et donc 1/6.
Ce dernier résultat démontrant que la valeur de est optimale pour l'extension de la zone de linéarité via l'injection d'un seul harmonique de rang 3. Enfin, pour démontrer l'extension de 15% il suffit de prendre la valeur précédente de 1/6, et de calculer pour quelle valeur de la modulante atteint de nouveau 0.5. Le maximum étant atteint pour un multiple entier relatif de on se retrouve avec :
Ce qui donne:
Ainsi le nouvel indice de modulation maximal atteignable avant saturation est ce qui correspond en effet à une augmentation d'environ 15% par rapport à l'indice de modulation précédent ().
MLI aléatoire
Le principe des MLI aléatoires (Random PWM ou RPWM en anglais) est de générer un grand nombre d'harmoniques afin de réduire le bruit ressenti. Plus précisément, il s'agit d'étaler sur l'ensemble des fréquences le spectre fréquentiel. Pour se faire, plusieurs méthodes sont décrites dans la littérature [4], mais la technique la plus simple reste de faire varier aléatoirement la fréquence de la porteuse triangulaire entre une fréquence maximale et une fréquence minimale définie par l'utilisateur. Cette technique permet ainsi de ne pas avoir des pics de puissance sur des harmoniques précis mais de les étaler sur tout le spectre. Cette configuration apporte ce qui semble être un paradoxe car mathématiquement, la puissance des harmoniques est en valeur absolue plus élevée. Mais l'oreille humaine n'est pas sensible à la puissance du bruit en tant que telle, elle est sensible à la puissance de certaines fréquences. Ainsi, étaler le spectre ne crée plus un bruit stridant mais un sentiment d'écoulement de sable fin bien plus agréable. Il est à noter que les RPWM ne peuvent fonctionner qu'à une fréquence de commutation élevée par rapport à la fréquence électrique afin de respecter la consigne de tension[5],[6],[4].
MLI Discontinue
Le principe des MLI discontinue (Discontinuous PWM or DPWM en anglais) a été introduit pour la première fois par Depenbrock en 1977 [7] en introduisant ce qui sera appelé plus tard la DPWM1. Le principal avantage des DPWM est de permettre de réduire les pertes par commutations des convertisseurs d'électronique de puissance en empêchant périodiquement une phase de commuter. Ce qui a pour effet de diminuer les pertes par commutation. Cependant, les mauvaises performances dans les faibles indices de modulation (problèmes d'impulsion trop étroites et la mauvaise qualité de la forme d'onde de courant) ainsi que la complexité de mise en œuvre de cette première stratégie ont limité l'application de cette méthode. Néanmoins, d'autres travaux plus récents ont conduit à d'autres mises en œuvre équivalentes et à des simplifications des stratégies DPWM[8],[9].
MLI « Vecteur spatial »
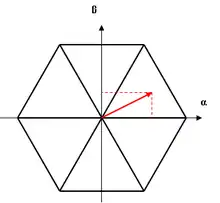
La MLI dite space vector (vecteur spatial, abrégé en SVM dans la littérature) est surtout applicable aux variateurs de vitesse triphasés sans neutre.
Elle consiste à considérer globalement le système triphasé, et à lui appliquer une transformée de Concordia pour se ramener dans le plan (Vα, Vβ). Le système triphasé de tensions à générer pour la durée d'échantillonnage en cours peut alors être représenté comme un unique vecteur dans ce plan (voir aussi commande vectorielle).
Ce vecteur n'est pas directement réalisable par les interrupteurs du variateur, mais on peut chercher les trois configurations les plus proches (situées sur les sommets et au centre de l'hexagone), et les appliquer successivement pendant une fraction adéquate de la période d'échantillonnage, de façon à obtenir en moyenne le vecteur recherché.
En modulation sinusoïdale, elle donne des résultats similaires (mais néanmoins meilleurs) à la MLI intersective à porteuse triangulaire centrée. Néanmoins, elle peut être plus facile à implanter dans un microcontrôleur, et, disjointe d'harmonique 3, elle permet de maximiser la puissance disponible, ce qui justifie son usage.
MLI « précalculée »
Les MLI précalculées aussi appelées MLI hors ligne ou Optimal Pulse pattern (OPP) en anglais est surtout utilisée lorsque, du fait d'une fréquence porteuse faible, on a besoin d'optimiser le spectre du signal généré. Le motif du signal de sortie est prédéterminé (hors ligne) et stocké dans des tables qui sont ensuite lues en temps réel.
De fait, ces MLI sont toujours synchrones (la fréquence porteuse est exactement multiple de la fréquence de la modulante), en effet l'optimisation réalisée en amont génère des angles de commutation bien précis qui ne peuvent être réalisés que de manière synchrone. De plus, le synchronisme est une condition nécessaire pour avoir un spectre harmonique constante et éviter la générations d'harmoniques plus faibles que le fondamental qui sont difficiles à filtrer[1]. En pratique, ce type de MLI ne peut être réalisé qu'en numérique, ou en analogique grâce à une carte FPGA.
Commande par hystérésis
Cette méthode consiste à élaborer le signal MLI directement à partir de la grandeur à contrôler, par des décisions de type tout ou rien. Son nom de "Hystérésis", vient du fait que le choix de la commande se décide grâce à plusieurs cycle d'hystérésis (une pour chaque phase). En effet, en pratique, une comparaison entre le courant de commande et le courant de sortie est faite. Ensuite cette différence, au delà d'un certain seuil fait changer la ou les cellules de commutation de l'état haut à l'état bas et vice versa.
Les avantages sont la très grande simplicité et le temps de réponse minimal aux perturbations. L'inconvénient majeur est l'absence de contrôle de la fréquence de commutation des transistors et sa forte non-linéarité intrinsèque, ce qui rend délicat leur dimensionnement.
Voir aussi
Articles connexes
- Modulation d'amplitude
- Modulation de fréquence
- Échantillonnage
- Mode de glissement
- Rapport cyclique d'ouverture (RCO)
Notes et références
- (en) Holmes, Pulse width modulation for power converters : Principles and practice, John Wiley & Sons, .
- (en) Buja, « Improvement of pulse width modulation techniques », Archiv fur Elektrotechnik, vol. 57, no 5, , p. 281 - 289 (lire en ligne).
- (en) Houldsworth et Grant, « The Use of Harmonic Distortion to Increase the Output Voltage of a Three-Phase PWM Inverter », IEEE Transactions on Industry Applications, vol. IA-20, no 5, , p. 1224-1228 (DOI 10.1109/TIA.1984.4504587, lire en ligne).
- (en) Trzynadlowski, « Random pulse width modulation techniques for converter-fed drive systems-a review », IEEE Transactions on Industry Applications, vol. 30, no 5, , p. 1166-1175 (DOI 10.1109/28.315226).
- (en) Gieras, Noise of Polyphase Electric Motors, CRC Press, coll. « Engineering & Technology », , 392 p. (ISBN 9781315220987, DOI 10.1201/9781420027730).
- (en) Habetler, « Acoustic noise reduction in sinusoidal pwm drives using a randomly modulated carrier », IEEE Transactions on Power Electronics, vol. 6, no 3, , p. 356-363 (DOI 10.1109/63.85902).
- (en) Depenbrock, « Pulse width control of a 3-phase inverter with non-sinusoidal phase voltages », Conf. Record of IEEE/IAS Annu. Meeting, , p. 399--403.
- (en) Hava, « A high-performance generalized discontinuous PWM algorithm », IEEE Transactions on Industry applications, vol. 34, no 5, , p. 1059--1071 (DOI 10.1109/28.720446, lire en ligne).
- (en) Ojo, « The generalized discontinuous PWM scheme for three-phase voltage source inverters », IEEE Transactions on Industrial Electronics, vol. 51, no 6, , p. 1280-1289 (DOI 10.1109/TIE.2004.837919, lire en ligne).
- Portail de l’électricité et de l’électronique