Nombre cyclique
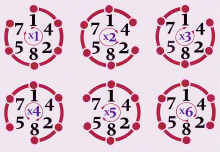
Un nombre cyclique, ou nombre phénix, est un entier naturel dont les permutations circulaires des chiffres correspondent aux multiples du nombre. Le plus connu est 142 857 :
- 142 857 × 1 = 142 857
- 142 857 × 2 = 285 714
- 142 857 × 3 = 428 571
- 142 857 × 4 = 571 428
- 142 857 × 5 = 714 285
- 142 857 × 6 = 857 142
Ne doit pas être confondu avec Nombre cyclique (théorie des groupes).
Cas spéciaux
Si les zéros ne sont pas permis au début des nombres, alors 142 857 est le seul nombre cyclique décimal. Mais s'ils sont permis, la suite des nombres cycliques commence comme suit :
| Chiffres | Nombre cyclique |
|---|---|
| 6 | 142 857 |
| 16 | 0 588 235 294 117 647 |
| 18 | 05 263 157 894 736 8421 |
| 22 | 0 434 782 608 695 652 173 913 |
| 28 | 0 344 827 586 206 896 551 724 137 931 |
| 46 | 0 212 765 957 446 808 510 638 297 872 340 425 531 914 893 617 |
| 58 | 0 169 491 525 423 728 813 559 322 033 898 305 084 745 762 711 864 406 779 661 |
| 60 | 016 393 442 622 950 819 672 131 147 540 983 606 557 377 049 180 327 868 852 459 |
| 96 | 010 309 278 350 515 463 917 525 773 195 876 288 659 793 814 432 989 690 721 649 484 536 082 474 226 804 123 711 340 206 185 567 |
Pour être cyclique, seuls les multiples successifs du nombre doivent être considérés et ceux-ci doivent correspondre à des permutations circulaires du nombre. Ainsi, le nombre 076923 n'est pas considéré comme cyclique, même si toutes ses permutations circulaires sont des multiples, car ceux-ci ne sont pas successifs :
- 076923 × 1 = 076923
- 076923 × 3 = 230769
- 076923 × 4 = 307692
- 076923 × 9 = 692307
- 076923 × 10 = 769230
- 076923 × 12 = 923076
Cette restriction exclut aussi des cas triviaux tels :
- chiffres répétés, par exemple : 555 ;
- nombres cycliques répétés, par exemple : 142 857 142 857 ;
- chiffres uniques précédés de zéros, par exemple : 005.
Les chiffres uniques peuvent être considérés comme des nombres cycliques triviaux ou dégénérés.
Relation avec les développements décimaux périodiques
Les nombres cycliques sont liés aux développements décimaux périodiques des fractions unitaires. Tout nombre cyclique de longueur L est le développement décimal de[1]
- 1/(L + 1).
Réciproquement, si la période du développement décimal de 1/p (où p est un nombre premier) est
- p − 1,
alors les chiffres représentent un nombre cyclique[1].
Par exemple :
- 1/7 = 0,142857142857…
Les multiples de ces fractions présentent des permutations circulaires[1]:
- 1/7 = 0,142857142857…
- 2/7 = 0,285714285714…
- 3/7 = 0,428571428571…
- 4/7 = 0,571428571428…
- 5/7 = 0,714285714285…
- 6/7 = 0,857142857142…
Formes de nombres cycliques
En s'appuyant sur leur relation aux fractions unitaires, on démontre que les nombres cycliques sont de la forme[1]
où b est la base (10 dans le cas du système décimal) et p est un nombre premier ne divisant pas b. Les nombres premiers p qui génèrent des nombres cycliques sont appelés nombres premiers longs.
Par exemple, le cas b = 10, p = 7 donne le nombre cyclique 142857.
Toutes les valeurs de p ne généreront pas forcément un nombre cyclique selon cette formule; par exemple p = 13 donne 076923076923. Ces cas erronés contiendront toujours une ou plusieurs répétitions de chiffres.
Les vingt premières valeurs de p pour lesquelles cette formule produit un nombre cyclique en notation décimale sont (suite A001913 de l'OEIS) :
- 7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, 179, 181, 193, 223, 229 et 233.
Cette suite intervient en théorie algébrique des nombres : elle est constituée des nombres premiers p tels que 10 est une racine primitive modulo p. Une conjecture d'Emil Artin postule que cette suite contiendrait 37,395..% des nombres premiers.
Construction des nombres cycliques
Les nombres cycliques peuvent être construits par l'algorithme suivant :
Soit b la base (10 en base décimale).
Soit p un nombre premier ne divisant pas b.
Soit t = 0.
Soit r = 1.
Soit n = 0.
Répéter ce qui suit :
- Soit t = t + 1
- Soit x = r · b
- Soit d = int(x / p)
- Soit r = x mod p
- Soit n = n · b + d
- Si r ≠ 1, répéter.
Si t = p − 1 alors n est un nombre cyclique.
Cette procédure fonctionne en calculant les décimales de 1/p en base b, par division longue. r est le reste à chaque étape et d est la décimale produite.
L'étape
- n = n · b + d
sert uniquement à colliger les chiffres. Dans les langages incapables d'opérer sur des nombres entiers très grands, les chiffres doivent être exprimés ou conservés autrement.
Il est notable que si t excède p/2, le nombre est forcément cyclique, sans besoin de calculer les chiffres restants.
Propriétés d'un nombre cyclique
- Le produit d'un nombre cyclique avec le nombre premier ayant servi à le générer consiste en une suite de chiffres 9. Par exemple, 142 857 × 7 = 999 999.
- L'addition de l'entier correspondant à la première moitié des chiffres d'un nombre cyclique à l'entier correspondant à la seconde moitié de ceux-ci consiste en une suite de chiffres 9 : 142 + 857 = 999.
- Un nombre cyclique est un nombre parasite.
- Un nombre cyclique tronqué après ses n premiers chiffres (non tous nuls) est une approximation par défaut de la fraction 10n/p. Si r est le reste entier de cette division, alors le nombre cyclique peut être produit en commençant par ses n premiers chiffres, puis en additionnant le r × le nombre précédemment additionné et décalé de n rangs vers la droite :
Exemple : pour p=7, le nombre cyclique est 142857142857...
- avec n=1 : 10 = 7 × 1 + 3 (1 = premier chiffre du nombre cyclique, reste r = 3)
- avec n=2 : 100 = 7 × 14 + 2 (14 = 2 premiers chiffres du nombre cyclique, reste r = 2)
- avec n=3 : 1000 = 7 × 142 + 6 (142 = 3 premiers chiffres du nombre cyclique, reste r = 6), etc.
et on peut écrire :
n=1 n=2 n=3
1 x3 14 x2 142 x6
3 | 28 | 852 |
9 v 56 v 5112 v
27 112 30672
81 224 184032
243 448 1104192
+ 729 + 896 + 6625152
--------- ---------------- -----------------------
1428... 14285714285... 1428571428571428...
Autres bases
En utilisant la technique décrite plus haut, on peut trouver les nombres cycliques d'autres bases arithmétiques.
En base binaire (suite A001122 de l'OEIS) :
| Chiffres | Nombre cyclique |
|---|---|
| 2 | 01 |
| 4 | 0 011 |
| 10 | 0 001 011 101 |
| 12 | 000 100 111 011 |
| 18 | 000 011 010 111 100 101 |
En base ternaire (suite A019334 de l'OEIS) :
| Chiffres | Nombre cyclique |
|---|---|
| 4 | 0 121 |
| 6 | 010 212 |
| 16 | 0 011 202 122 110 201 |
| 18 | 001 102 100 221 120 122 |
| 28 | 0 002 210 102 011 122 200 121 202 111 |
En base octale (suite A019338 de l'OEIS) :
| Chiffres | Nombre cyclique |
|---|---|
| 2 | 25 |
| 4 | 1 463 |
| 10 | 0 564 272 135 |
| 28 | 0 215 173 454 106 475 626 043 236 713 |
| 52 | 0 115 220 717 545 336 140 465 103 476 625 570 602 324 416 373 126 743 |
En base duodécimale (suite A019340 de l'OEIS) :
| Chiffres | Nombre cyclique |
|---|---|
| 4 | 2 497 |
| 6 | 186 A35 |
| 16 | 0 857 921 4B3 642 9A7 |
| 30 | 047 8AA 093 598 166 B74 311 B28 623 A55 |
| 40 | 0 361 90A 653 277 397 A9B 4B8 5A2 B15 689 448 241 207 |
En base 24 (notation en utilisant les lettres de A à N) (suite A019351 de l'OEIS) :
| Chiffres | Nombre cyclique |
|---|---|
| 6 | 3A6 KDH |
| 10 | 2 48H ALJ F6D |
| 12 | 1K7 95C M3G EIB |
| 16 | 1 9L4 5FC GME 2JI 8B7 |
| 30 | 0ID MAK 327 HJ8 C96 N5A 1D3 KLG 64F BEH |
Noter qu'en notation ternaire (b = 3), le cas p = 2 génère 1 comme nombre cyclique. Bien que les chiffres uniques puissent être considérés comme des cas triviaux, il peut être utile, pour la complétude de la théorie, de les considérer, mais uniquement lorsqu'ils sont générés de cette façon.
On peut démontrer qu'aucun nombre cyclique (autre que les chiffres uniques triviaux) d'aucune base arithmétique n'est un carré parfait ; ainsi il n'y a aucun nombre cyclique en base hexadécimale.
Voir aussi
Références
- Pascal Boyer, Petit compagnon des nombres et de leurs applications, Paris, Calvage et Mounet, , 648 p. (ISBN 978-2-916352-75-6), I. Arithmétique de ℤ, chap. 2.4 (« Développement décimal de 1/p, d'après J. Germoni »), p. 28-34.
Articles connexes
Bibliographie
- (en) Martin Gardner, Mathematical Circus: More Puzzles, Games, Paradoxes and Other Mathematical Entertainments From Scientific American, New York, MAA, 1979, p. 111-122
- (en) Dan Kalman, « Fractions with Cycling Digit Patterns », The College Mathematics Journal (en), vol. 27, no 2, 1996, p. 109-115
- (en) John Leslie, The Philosophy of Arithmetic, Longman, Hurst, Rees, Orme, and Brown, 1820, [lire en ligne]
- (en) David Wells, The Penguin Dictionary of Curious and Interesting Numbers (en), Penguin Press (ISBN 0-14-008029-5)
Lien externe
(en) Eric W. Weisstein, « Cyclic Number », sur MathWorld
Crédit d'auteurs
- Arithmétique et théorie des nombres