Optique géométrique

L’optique géométrique est une branche de l'optique qui s'appuie notamment sur le modèle du rayon lumineux. Cette approche simple permet entre autres des constructions géométriques d’images, d’où son nom. Elle constitue l'outil le plus flexible et le plus efficace pour traiter les systèmes dioptriques et catadioptriques. Elle permet ainsi d'expliquer la formation des images.

Pour les articles homonymes, voir Optique (homonymie).

L'optique géométrique (la première théorie optique formulée) se trouve validée a posteriori par l'optique ondulatoire, en faisant l'approximation que tous les éléments utilisés sont de grande dimension devant la longueur d'onde de la lumière[1].

Dans le débat entourant au XIXe siècle la dualité onde-corpuscule de la lumière, l'optique géométrique ne spécifie pas la nature de la lumière et est alors compatible avec les deux approches[2].

Historique

Du point de vue physique, l'optique géométrique est une approche alternative à l'optique ondulatoire (souvent appelée optique physique) et à l'optique quantique. Elle est en revanche plus ancienne, ayant été développée dès l'Antiquité. La notion de rayon lumineux a ainsi été introduite par Euclide au IVe siècle avant notre ère[3].

Jusqu'au XVIe siècle, l'optique reste sur cette notion de rayon lumineux et ne progresse que de manière empirique, permettant toutefois l'apparition de premiers verres correcteurs en 1285. Les lois de Snell-Descartes sont trouvées par Snell en 1621 puis par Descartes en 1637[4].

La première expérience montrant les limites de l'optique géométrique est réalisée par Grimaldi en 1665 qui donne son nom à la diffraction. L'optique ondulatoire ne sera mise en évidence qu'au XIXe siècle avec l'expérience des fentes d'Young et l'optique quantique n'émergera qu'au cours du XXe siècle.

Propagation de la lumière

Le rayon lumineux
Vue d'artiste de la notion empirique de rayon lumineux

Un rayon lumineux est un objet théorique : il n'a pas d'existence physique. Il sert de modèle de base à l'optique géométrique où tout faisceau de lumière est représenté par un ensemble de rayons lumineux. Le rayon lumineux est l'approximation de la direction de propagation de l'onde lumineuse ou des photons.

Lorsque l'on considère l'onde lumineuse, si la surface d'onde est un plan, tous les rayons sont parallèles entre eux et si la surface d'onde est sphérique, tous les rayons se dirigent vers un point, ou semblent provenir d'un point : on a un faisceau qui converge en un point, ou qui diverge à partir d'un point.

Le chemin optique

La notion de chemin optique permet de traduire de manière géométrique l'influence de l'indice de réfraction des milieux sur la vitesse de la lumière. Le chemin optique est égal à la distance que la lumière aurait parcourue pendant le même temps dans le vide.

En pratique, dans un milieu homogène d'indice , pour une distance parcourue , le chemin optique s'exprime :

.

Dans une approche continue et non discrète du chemin optique : [5].

Le principe de Fermat s'appuie sur cette notion de chemin optique : « entre 2 points, la lumière suit le trajet correspondant à un chemin optique stationnaire (constant) c'est-à-dire le chemin avec le temps de parcours minima[6] ».

Lien entre la notion de rayon lumineux et la théorie ondulatoire
Propagation d'un front d'onde plan

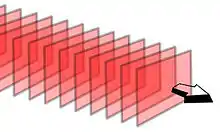
Pour relier le modèle du rayon lumineux à la théorie ondulatoire de la lumière, il faut avoir une approche énergétique de la propagation de la lumière. Le rayon lumineux représente la direction de propagation de l'énergie lumineuse. Cette direction est orthogonale aux fronts d'onde de l'onde lumineuse[7].

Lois de l'optique géométrique

Deux grands principes ont fondé l'optique géométrique :

  • le principe de Fermat qui énonce que le trajet de la lumière est toujours un extremum, donc que le rayon lumineux passera toujours par le trajet le plus rapide ou un point col (ou le plus long parmi les chemins respectant des contraintes imposées) ;
  • le principe du retour inverse de la lumière énonçant que le trajet d'un rayon lumineux peut être parcouru dans les deux sens.

Ces principes n'ont été formalisés que tardivement comparé à la loi de la réflexion mais ils avaient déjà été postulés dans l'Antiquité par Héron d'Alexandrie[8]. La loi de la réfraction est arrivée plus tard. Réflexion et réfraction sont gouvernées par les lois de Snell-Descartes. Le phénomène de réfraction limite et de réflexion totale ne seront trouvés que plus tard.

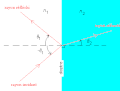  • La réfraction en optique géométrique sur un dioptre plan, dans le cas où n1 < n2.
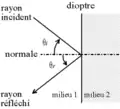  • Illustration de la loi de la réflexion.

Domaine de validité de l'optique géométrique

L'optique géométrique ne permet pas d'expliquer tous les phénomènes lumineux. En particulier, elle ne tient pas compte du fait que la lumière est de nature ondulatoire ou corpusculaire. Lorsque tous les objets qui interagissent avec la lumière ont des tailles caractéristiques grandes devant la longueur d'onde du rayon lumineux alors il est convenable et plus simple d'utiliser l'optique géométrique pour décrire son comportement avec une bonne précision. Mais quand la lumière diffuse ou passe à travers des objets dont la taille est du même ordre de grandeur (voire plus petits) que sa longueur d'onde, alors il n'est plus possible de négliger l'aspect ondulatoire et on entre dans le domaine de l'optique physique.

Deux phénomènes caractéristiques de l'optique ondulatoire, inexplicables dans le contexte de l'optique géométrique, sont les interférences lumineuses et la diffraction.

Autres modèles de l'optique et interaction avec le modèle géométrique

Dans le modèle électromagnétique de la lumière, l'optique géométrique correspond à un cas particulier où la longueur d'onde est considérée nulle devant tous les systèmes (lentilles, miroirs, ...) et où les rayons sont considérés comme tous incohérents entre eux[9]. Cette approximation permet de justifier la focalisation des rayons lumineux en un point ainsi que l'absence de phénomène de diffraction.

Notes et références
  1. Optique géométrique sur Google Livres
  2. Optique géométrique : memento sur Google Livres
  3. Optique géométrique sur Google Livres
  4. Optique MPSI-PCSI-PTSI sur Google Livres
  5. Physique PC-PC* sur Google Livres
  6. Cours d'optique de l'Université d'Aix-Marseille
  7. Optique MPSI-PCSI-PTSI sur Google Livres
  8. Optique géométrique : imagerie et instruments sur Google Livres
  9. Physique PC-PC* sur Google Livres

Voir aussi

Autres modèles optique

Articles liés

Liens externes
  • Portail de la physique
  • Portail de l’optique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.