Phénomène périodique

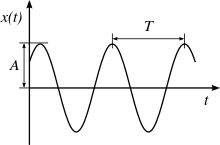
On appelle phénomène périodique un phénomène qui se répète de façon identique au bout d'un intervalle de temps régulier. La période d'un phénomène périodique est la plus petite durée séparant deux reproductions à l'identique du phénomène ; elle est souvent notée . On dit souvent qu'au cours d'une période le système effectue un cycle. Dans le système international d'unités (SI), la période d'un phénomène s'exprime en secondes.

« Période (physique) » redirige ici. Pour les autres significations, voir période.

Période
Amplitude et période d'une onde.
Unités SI seconde (s)
Dimension
Nature Grandeur scalaire intensive
Symbole usuel
Lien à d'autres grandeurs

Le nombre de cycles effectués par unité de temps est appelé la fréquence, habituellement notée . La fréquence s'exprime en hertz dans le SI. La période et la fréquence sont l'inverse l'une de l'autre : ou, de façon équivalente, .

Dans le cas des phénomènes ondulatoires, c'est-à-dire pour lesquels une perturbation se propage dans l'espace, la période peut être calculée par la relation , où est la période de l'onde (exprimée en secondes dans le SI), la longueur d'onde (en mètres dans le SI) et la célérité de l'onde (en mètres par seconde dans le SI).

Dans divers domaines, on préfère raisonner en termes de pulsation (appelée aussi fréquence angulaire), qui s'exprime en radians par seconde. Fréquence et pulsation sont liées par la relation suivante :

Description

Le phénomène périodique le plus simple du point de vue mathématique se présente comme une variation sinusoïdale. C'est, en particulier, le cas d'un son pur, variation sinusoïdale de la pression de l'air, caractérisé par sa hauteur et son intensité, c'est-à-dire par sa fréquence et son amplitude. Ce son pur est peu utilisé en musique où chaque instrument présente un timbre particulier associé à une variation de la pression plus compliquée qu'une sinusoïde.

Celle-ci peut s'interpréter comme la superposition d'un son fondamental dont la fréquence définit la hauteur et d'harmoniques ayant des fréquences multiples de celle-ci. Cette décomposition se traduit mathématiquement par la notion de série de Fourier.

Il y a aussi un phénomène tout à fait naturel que toute personne vivante peut avoir. Le battement de cœur, un phénomène périodique.

Exemples d'application

De nombreux cycles à oscillations périodiques sont présents dans la nature.

  • Les ondes représentent une grande classe de phénomènes périodiques qui ont la propriété de se répéter plusieurs fois, à la fois dans l'espace et dans le temps. Parmi de nombreux exemples on trouve le courant alternatif dans le domaine de l'électricité, dont la fréquence est de l'ordre de 50 Hz en Europe et de 60 Hz en Amérique du Nord, le son qui est une onde mécanique, la lumière qui est une onde électromagnétique.
  • Les marées, dans lesquelles les mouvements relatifs de la Terre, de la Lune et du Soleil font apparaître diverses périodes dont la plus courte est d'environ 12 h.
  • Le cycle diurne (lever et coucher du soleil), d'une période de 24 h.
  • Les conjonctions planétaires, les éclipses, le dépassement littéral des comètes et tous les phénomènes astronomiques liés aux orbites des astres.
  • Certains cycles elliptiques touchant au corps: le rythme cardiaque, les ondes cérébrales, etc.
  • Dans le corps humain, de nombreux phénomènes périodiques se répètent tels que les battements du cœurs, des paupières, etc. Étudier les signaux périodiques émis par notre organisme peut permettre d'établir des diagnostics médicaux :
  • L'électrocardiographie (ECG) permet d'étudier les rythmes cardiaque et peut déceler certains troubles de ce dernier tels que la tachycardie (accélération du rythme cardiaque) ou encore la bradycardie (ralentissement du rythme cardiaque) et même la fibrillation (désorganisation complète du rythme cardiaque).
  • L'électroencéphalographie permet d'étudier les signaux électriques émis par le cerveau . Cette méthode permet de localiser des zones du cerveau défectueuses.

Articles connexes
  • Portail de la physique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.