Processus d'Ornstein-Uhlenbeck
En mathématiques, le processus d'Ornstein-Uhlenbeck, nommé d'après Leonard Ornstein et George Uhlenbeck[1] et aussi connu sous le nom de mean-reverting process, est un processus stochastique décrit par l'équation différentielle stochastique
où θ, μ et σ sont des paramètres déterministes et Wt est le processus de Wiener.
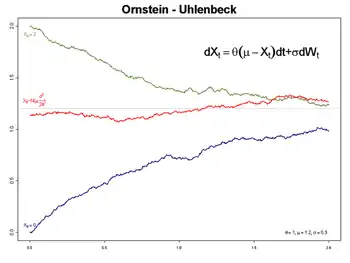
Bleu : Valeur initiale a=0 (p. s.)
Vert : Valeur initiale a=2 (p. s.)
Rouge : Valeur initiale distribuée normalement ainsi le procédé a une mesure invariante
Solution
Cette équation est résolue par la méthode de variation des constantes. Appliquons le lemme d'Itō à la fonction pour obtenir
En intégrant de 0 à t, on obtient
d'où nous voyons
Ainsi, le premier moment est donné (en supposant que est une constante) par :
On peut utiliser l'isométrie d'Itō (en) pour calculer la covariance
Il est aussi possible (et souvent commode) de représenter (sans condition) en tant que mesure transformée du temps du processus Wiener :
ou avec condition ( donné) comme
Le processus d'Ornstein-Uhlenbeck (un exemple de processus gaussien à variance bornée) admet une distribution de probabilité stationnaire, contrairement au processus de Wiener.
L'intégrale temps de ce processus peut être utilisée pour générer un bruit avec un spectre de puissance 1/f.
Application
Le modèle de Vasicek (en) des taux d'intérêt est un exemple de processus d'Ornstein-Uhlenbeck où les coefficients sont positifs et constants.
Le Processus CIR, le modèle de Cox, Ingersoll et Ross (1985) est une extension du modèle de Vasicek et du processus d'Ornstein-Uhlenbeck qui introduit la racine carrée du taux d'intérêt instantané dans le coefficient du terme stochastique.
Références
- (en) G. E. Uhlenbeck et L. S. Ornstein, « On the Theory of Brownian Motion », Physical Review, vol. 36, , p. 823-841
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Ornstein–Uhlenbeck process » (voir la liste des auteurs).
- Portail des mathématiques