Régularité par morceaux

Cette fonction n'est pas continue sur ℝ. En revanche, elle y est continue par morceaux.

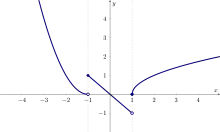
Une fonction f est continue par morceaux sur le segment [a, b] s’il existe une subdivision σ : a = a₀ < … < a_n = b telle que les restrictions de f à chaque intervalle ouvert ]a_i, a_{i + 1}[ admettent un prolongement continu à l'intervalle fermé [a_i, a_{i + 1}].

Toute fonction continue sur un segment étant réglée, les fonctions continues par morceaux sur [a, b] le sont également.

Concrètement une telle fonction f est continue sur ]a_i,a_i+1[ et admet une limite finie à droite et à gauche en chaque a_i (lesquelles peuvent être distinctes et distinctes de la valeur de f au point a_i lui-même).

On définit de même les fonctions de classe C^k par morceaux, linéaires par morceaux, etc. On notera qu'une fonction de classe C¹ par morceaux, par exemple, n'est pas nécessairement continue en a_i, mais qu'elle et sa dérivée admettent des limites finies à droite et à gauche en a_i.

Cette notion s'étend naturellement pour les fonctions définies sur un intervalle quelconque : une fonction est dite continue (ou autre propriété) par morceaux sur l'intervalle I quand elle est continue (ou autre) par morceaux sur tout segment de I.

Soient Ω un ouvert borné de ℝⁿ et Ω son adhérence.

Pour simplifier, supposons que Ω est un domaine « régulier » (par exemple et pour fixer les idées, que le théorème de la divergence est valable pour toute fonction suffisamment lisse sur ℝⁿ).

Alors :

• une fonction f de Ω dans ℝ est continue par morceaux — noté C⁰
  _I(Ω) — s'il existe un ensemble fini d'ouverts disjoints Ω_i tels que ${\displaystyle {\overline {\Omega }}=\cup _{i}{\overline {\Omega _{i}}}}$ et que la restriction de f à chacun des Ω_i admette un prolongement continu à ℝⁿ ;
• une fonction f de Ω dans ℝ est de classe C^k par morceaux — noté C^k
  _I(Ω) — si elle est de classe C^k–1 et s'il existe un ensemble fini d'ouverts disjoints Ω_i tels que ${\displaystyle {\overline {\Omega }}=\cup _{i}{\overline {\Omega _{i}}}}$ et que la restriction de f à chacun des Ω_i soit de classe C^k(Ω_i).

La régularité par morceaux est utilisée pour démontrer les résultats importants de certaines théories simplifiées de l'intégration, et leurs applications, comme l'analyse par séries de Fourier.

• Fonction affine par morceaux
• Application linéaire par morceaux

• Portail de l'analyse