Application linéaire par morceaux
En mathématiques, une application linéaire[1] par morceaux est une application définie sur un espace topologique composé de facettes affines, à valeurs dans un espace affine et dont les restrictions à chaque facette sont induites par des applications affines. Une telle application est en général supposée continue.
Ne pas confondre avec la notion de fonction affine par morceaux en analyse.
Un cas particulier d'application linéaire par morceaux est celui d'une fonction affine par morceaux, définie sur une réunion d'intervalles réels et à valeurs réelles, telle que la restriction à chacun de ces intervalles est donnée par une expression affine.
La notion est cependant développée surtout pour décrire des polyèdres et plus généralement les complexes simpliciaux et variétés PL. Elle sert en imagerie numérique pour représenter des objets en trois dimensions.
Définition
Une application linéaire par morceaux est une application f : Ω → V, où V est un espace affine réel et Ω est un espace topologique obtenu comme réunion d'une famille de parties homéomorphes à des parties d'un espace affine et de façon que les structures affines coïncident sur les intersections de ces parties et que les restrictions de f soient affines sur chaque partie.
La réunion peut être supposée finie et chacune de ces parties de Ω identifiée avec un polytope convexe.
- Exemples
Les fonctions valeur absolue, partie fractionnaire, signal triangulaire sont des exemples de fonctions linéaires par morceaux.
Applications
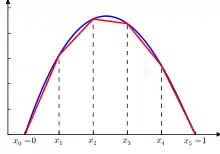
Les fonctions linéaires par morceaux sont utilisées pour obtenir des approximations de fonction : à partir d'un ensemble fini de valeurs ponctuelles d'une fonction donnée, on construit la fonction linéaire par morceaux qui interpole deux points successifs par une approximation linéaire.
Notes et références
- L'adjectif « linéaire » vient de la traduction de l'anglais piecewise linear mais correspond plus à la notion de fonction affine que de fonction linéaire.
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Piecewise linear function » (voir la liste des auteurs).
- Portail de la géométrie