Réseau neuronal convolutif

En apprentissage automatique, un réseau de neurones convolutifs ou réseau de neurones à convolution (en anglais CNN ou ConvNet pour convolutional neural networks) est un type de réseau de neurones artificiels acycliques (feed-forward), dans lequel le motif de connexion entre les neurones est inspiré par le cortex visuel des animaux. Les neurones de cette région du cerveau sont arrangés de sorte qu'ils correspondent à des régions qui se chevauchent lors du pavage du champ visuel[1]. Leur fonctionnement est inspiré par les processus biologiques[2], ils consistent en un empilage multicouche de perceptrons, dont le but est de prétraiter[3] de petites quantités d'informations. Les réseaux neuronaux convolutifs ont de larges applications dans la reconnaissance d'image et vidéo, les systèmes de recommandation[4] et le traitement du langage naturel[5].

Pour les articles homonymes, voir CNN.

Présentation

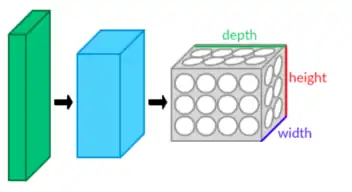
Considérons l'analyse d'une image monochrome (en 2 dimensions, largeur et hauteur) ou en couleur (en 3 dimensions, en considérant l'image RVB avec 3 unités de profondeurs, dont la troisième correspond à l'empilement de 3 images selon chaque couleur, rouge, verte et bleue).

Un réseau neuronal convolutif se compose de deux types de neurones artificiels, agencés en « couches » traitant successivement l'information :

Exemple d'image (gauche) et de son traitement par DeepDream (droite).
  • les neurones de traitement, qui traitent une portion limitée de l'image (appelée « champ réceptif ») au travers d'une fonction de convolution.
  • les neurones de mise en commun des sorties dits de pooling (totale ou partielle).

Un traitement correctif non linéaire et ponctuel peut être appliqué entre chaque couche pour améliorer la pertinence du résultat[6].

L'ensemble des sorties d'une couche de traitement permet de reconstituer une image intermédiaire, qui servira de base à la couche suivante.

Traitement de profondeur 1 et sans chevauchement (facilitant la compréhension)

Dans le cadre de la reconnaissance d'image, cette dernière est « pavée », c'est-à-dire découpée en petites zones (appelées tuiles). Chaque tuile sera traitée individuellement par un neurone artificiel (qui effectue une opération de filtrage classique en associant un poids à chaque pixel de la tuile). Tous les neurones ont les mêmes paramètres de réglage. Le fait d'avoir le même traitement (mêmes paramètres), légèrement décalé pour chaque champ récepteur, s'appelle une convolution[7],[8]. Cette strate de neurones avec les mêmes paramètres est appelée « noyau de convolution ».

Les pixels d'une tuile sont analysés globalement. Dans le cas d'une image en couleur, un pixel contient 3 entrées (rouge, vert et bleu), qui seront traitées globalement par chaque neurone. Donc l'image peut être considérée comme un volume, et notée par exemple 30 × 10 × 3 pour 30 pixels de largeur, 10 de hauteur et 3 de profondeur correspondant aux 3 canaux rouge, vert et bleu. De manière générale, on parlera de « volume d'entrée ».

Généralisation (profondeur et chevauchement)

Dans les faits, la zone analysée est légèrement plus grande que la tuile et est appelée « champ récepteur ». Les champs récepteurs se chevauchent donc, afin d'obtenir une meilleure représentation de l'image originale ainsi qu'une meilleure cohérence du traitement au fil des couches de traitement[9]. Le chevauchement est défini par le pas (décalage entre deux champs récepteurs adjacents).

Un noyau de convolution va analyser une caractéristique de l'image d'entrée. Pour analyser plusieurs caractéristiques, on va empiler des strates de noyaux de convolution indépendants, chaque strate analysant une caractéristique de l'image. L'ensemble des strates ainsi empilées forme la « couche de traitement convolutif », qu'il faut voir en fait comme un volume (souvent appelé « volume de sortie »). Le nombre de strates de traitement s'appelle la profondeur de la couche de convolution (à ne pas confondre avec la profondeur d'un réseau de neurones convolutifs qui compte le nombre de couches de convolution).

Une couche de convolution permet de traiter un volume d'entrée pour fournir un volume de sortie. On peut également assimiler le volume de sortie à une image intermédiaire.

Pour formuler les choses différemment, dans un réseau de neurones convolutifs, chaque champ récepteur est traité par un perceptron monocouche. Et tous les perceptrons monocouche associés à l'ensemble des champs récepteurs sont paramétrés de manière identique.

Caractéristiques et avantages

Un avantage majeur des réseaux convolutifs est l'utilisation d'un poids unique associé aux signaux entrant dans tous les neurones d'un même noyau de convolution. Cette méthode réduit l'empreinte mémoire, améliore les performances[3] et permet une invariance du traitement par translation. C'est le principal avantage du réseau de neurones convolutifs par rapport au perceptron multicouche, qui, lui, considère chaque neurone indépendant et affecte donc un poids différent à chaque signal entrant.

Lorsque le volume d'entrée varie dans le temps (vidéo ou son), il devient intéressant de rajouter un paramètre le long de l'échelle de temps dans le paramétrage des neurones. On parlera dans ce cas de réseau neuronal à retard temporel (TDNN)[10].

Comparés à d'autres algorithmes de classification d'image, les réseaux de neurones convolutifs utilisent relativement peu de pré-traitement. Cela signifie que le réseau est responsable de faire évoluer tout seul ses propres filtres (apprentissage sans supervision), ce qui n'est pas le cas d'autres algorithmes plus traditionnels. L'absence de paramétrage initial et d'intervention humaine est un atout majeur des CNN.

Histoire

La conception des réseaux de neurones convolutifs suit la découverte de mécanismes visuels dans les organismes vivants. Début 1968, des travaux[11] ont montré chez l'animal que le cortex visuel contient des arrangements complexes de cellules, responsables de la détection de la lumière dans les sous-régions du champ visuel qui se chevauchent, appelés champs réceptifs. Le document a identifié deux types de cellules de base : les cellules simples, qui répondent à des pics caractéristiques (grand contraste, forte intensité...) à l'intérieur de leur champ récepteur ; et les cellules complexes, qui ont des champs récepteurs plus grands et sont localement invariantes à la position exacte du motif. Ces cellules agissent comme des filtres locaux sur l'espace d'entrée.

Le néocognitron

Le néocognitron (en), ancêtre des réseaux de convolution[12], a été décrit dans un document de 1980[6],[13]. C'est le premier véritable réseau de convolution parce qu'il force les unités situées en plusieurs positions d'avoir les mêmes poids. Sa version précédente, le cognitron, en différait principalement par l'absence de cette contrainte, mais possédait toutefois lui aussi des couches de pooling.

Le néocognitron a été modifié en 1988 pour les signaux temporels[14]. Sa conception a été améliorée en 1998[15], généralisée en 2003[16], et simplifiée dans la même année[17].

Une conception différente des réseaux de neurones convolutifs a été proposée en 1988[18] pour l'application de la décomposition en signaux d'électromyographies unidimensionnelles. Ce système a été modifié en 1989 grâce à d'autres conceptions à base de convolution[19],[20].

Réseaux de neurones convolutifs et processeurs graphiques

Suite à l'article de 2005 qui a établi l'intérêt des processeurs graphiques (GPU) pour l'apprentissage machine[21], plusieurs publications vont développer ce principe pour rendre les GPU très efficaces[22],[23],[24],[25]. En 2012, Ciresan et al. ont significativement amélioré la meilleure performance dans la littérature pour plusieurs bases de données d'images, y compris la base de données MNIST, la base de données noRb, le HWDB1, l'ensemble de données CIFAR10 (60 000 images 32 × 32 RVB étiquetées)[6], et l'ensemble de données ImageNet[26].

Différence entre réseaux de neurones convolutifs comparés et perceptron multicouche

Bien qu'efficaces pour le traitement d'images, les perceptrons multicouches (MLP) ont des difficultés à gérer des images de grande taille, en raison de la croissance exponentielle du nombre de connexions avec la taille de l'image, du fait que chaque neurone est « totalement connecté » à chacun des neurones de la couche précédente et suivante. Les réseaux de neurones convolutifs, dont le principe est inspiré de celui du cortex visuel des vertébrés, limite au contraire le nombre de connexions entre un neurone et les neurones des couches adjacentes, ce qui diminue drastiquement le nombre de paramètres à apprendre[27]. Pour un réseau profond tel que AlexNet par exemple, plus de 90 % des paramètres à apprendre sont dus aux 3 couches « complètement connectées » les plus profondes, et le reste concerne les (5) couches convolutives.

Une couche du CNN en 3 dimensions.(vert = volume d'entrée, bleu = volume du champ récepteur, gris = couche de CNN, cercles = neurones artificiels indépendants)

Par exemple, si on prend une image de taille 32 × 32 × 3 (32 de large, 32 de haut, 3 canaux de couleur), un seul neurone entièrement connecté dans la première couche cachée du MLP aurait 3 072 entrées (32*32*3). Une image 200 × 200 conduirait ainsi à traiter 120 000 entrées par neurone ce qui, multiplié par le nombre de neurones, devient énorme.

Les réseaux de neurones convolutifs visent à limiter le nombre d'entrées tout en conservant la forte corrélation « spatialement locale » des images naturelles. Par opposition aux MLP, les CNN ont les traits distinctifs suivants[28] :

  1. Connectivité locale : grâce au champ récepteur qui limite le nombre d'entrées du neurone, tout en conservant l'architecture MLP (cf. point précédent), les réseaux de neurones convolutifs assurent ainsi que les « filtres » produisent la réponse la plus forte à un motif d'entrée spatialement localisé, ce qui conduit à une représentation parcimonieuse de l'entrée. Une telle représentation occupe moins d'espace en mémoire. De plus, le nombre de paramètres à estimer étant réduit, leur estimation (statistique) est plus robuste pour un volume de données fixé (comparé à un MLP).
  2. Poids partagés : dans les réseaux de neurones convolutifs, les paramètres de filtrage d'un neurone (pour un champ récepteur donné) sont identiques pour tous les autres neurones d'un même noyau (traitant tous les autres champs récepteurs de l'image). Ce paramétrage (vecteur de poids et biais) est défini dans une « carte de fonction ».
  3. Invariance à la translation : comme tous les neurones d'un même noyau (filtre) sont identiques, le motif détecté par ce noyau est indépendant de localisation spatiale dans l'image

Ensemble, ces propriétés permettent aux réseaux de neurones à convolution d'obtenir une meilleure robustesse dans l'estimation des paramètres[28] sur des problèmes d'apprentissage puisque, pour une taille de corpus d'apprentissage fixée, la quantité de données par paramètres est plus grande. Le partage de poids permet aussi de réduire considérablement le nombre de paramètres libres à apprendre, et ainsi les besoins en mémoire pour le fonctionnement du réseau. La diminution de l'empreinte mémoire permet l'apprentissage de réseaux plus grands donc souvent plus puissants.

Blocs de construction

Une architecture de réseau de neurones convolutifs est formée par un empilement de couches de traitement :

  • la couche de convolution (CONV) qui traite les données d'un champ récepteur ;
  • la couche de pooling (POOL), qui permet de compresser l'information en réduisant la taille de l'image intermédiaire (souvent par sous-échantillonnage) ;
  • la couche de correction (ReLU), souvent appelée par abus « ReLU » en référence à la fonction d'activation (Unité de rectification linéaire) ;
  • la couche « entièrement connectée » (FC), qui est une couche de type perceptron ;
  • la couche de perte (LOSS).
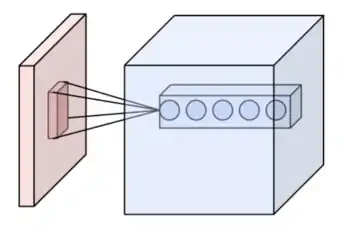    Ensemble de neurones (cercles) créant la profondeur d'une couche de convolution (bleu). Ils sont liés à un même champ récepteur (rouge).

Couche de convolution (CONV)

La couche de convolution est le bloc de construction de base d'un CNN. Le détail de son fonctionnement est précisé dans les paragraphes suivants.

Paramétrage

Trois hyperparamètres permettent de dimensionner le volume de la couche de convolution (aussi appelé volume de sortie) : la profondeur, le pas et la marge.

  1. Profondeur de la couche : nombre de noyaux de convolution (ou nombre de neurones associés à un même champ récepteur).
  2. Le pas contrôle le chevauchement des champs récepteurs. Plus le pas est petit, plus les champs récepteurs se chevauchent et plus le volume de sortie sera grand.
  3. La marge (à 0) ou zero padding : parfois, il est commode de mettre des zéros à la frontière du volume d'entrée. La taille de ce zero-padding est le troisième hyperparamètre. Cette marge permet de contrôler la dimension spatiale du volume de sortie. En particulier, il est parfois souhaitable de conserver la même surface que celle du volume d'entrée.

Si le pas et la marge appliquée à l'image d'entrée permettent de contrôler le nombre de champs récepteurs à gérer (surface de traitement), la profondeur permet d'avoir une notion de volume de sortie, et de la même manière qu'une image peut avoir un volume, si on prend une profondeur de 3 pour les trois canaux RVB d'une image couleur, la couche de convolution va également présenter en sortie une profondeur. C'est pour cela que l'on parle plutôt de « volume de sortie » et de « volume d'entrée », car l'entrée d'une couche de convolution peut être soit une image soit la sortie d'une autre couche de convolution.

La taille spatiale du volume de sortie peut être calculée en fonction de la taille du volume d'entrée , la surface de traitement (nombre de champs récepteurs), le pas avec lequel ils sont appliqués, et la taille de la marge . La formule pour calculer le nombre de neurones du volume de sortie est .

Si n'est pas entier, les neurones périphériques n'auront pas autant d'entrée que les autres. Il faudra donc augmenter la taille de la marge (pour recréer des entrées virtuelles).

Souvent, on considère un pas S=1, on calcule donc la marge de la manière suivante : si on souhaite un volume de sortie de même taille que le volume d'entrée. Dans ce cas particulier la couche est dite « connectée localement ».

Partage des paramètres

Le partage des paramètres de filtrage entre les différents neurones d'un même noyau de convolution (patch) permet au réseau de neurones convolutifs d'avoir la propriété d'invariance de traitement par translation. Il repose sur une hypothèse raisonnable : si un filtre est efficace en haut à gauche de l'image, il sera sûrement aussi efficace en bas à droite. Les valeurs du filtre (le patch) doivent être donc partagées par tous les neurones de la couche de convolution.

Si un élément du patch est utile au calcul à une certaine position dans l'espace, alors il devrait également être utile à une position différente. En d'autres mots, en considérant une strate bidimensionnelle (de profondeur 1) de la couche de convolution, tous ses neurones auront les mêmes poids et biais.

Étant donné que tous les neurones dans une seule tranche (noyau) de profondeur partagent le même paramétrage (patch), on considère que ces patchs opèrent une convolution avec l'entrée. Le résultat de cette convolution est une image intermédiaire. Plusieurs couples noyau/patchs permettent de construire une couche de traitement et produisent une image intermédiaire. Plusieurs couches de traitement peuvent être empilés pour produire l'image finale.

Dans les cas où l'image analysée a une structure spatiale définie (un visage par exemple avec les yeux en haut, le menton en bas, etc.), l'hypothèse du partage des paramètres perd de son sens. Dans ce cas, il est courant d'assouplir le système de partage des paramètres, et remplacer la couche de convolution par une couche connectée localement.

Couche de pooling (POOL)
Max pooling avec un filtre 2 × 2 et un pas de 2.

Un autre concept important des CNNs est le pooling (« mise en commun »), ce qui est une forme de sous-échantillonnage de l'image. L'image d'entrée est découpée en une série de rectangles de n pixels de côté ne se chevauchant pas (pooling). Chaque rectangle peut être vu comme une tuile. Le signal en sortie de tuile est défini en fonction des valeurs prises par les différents pixels de la tuile.

Le pooling réduit la taille spatiale d'une image intermédiaire, réduisant ainsi la quantité de paramètres et de calcul dans le réseau. Il est donc fréquent d'insérer périodiquement une couche de pooling entre deux couches convolutives successives d'une architecture de réseau de neurones convolutifs pour réduire le sur-apprentissage. L'opération de pooling crée aussi une forme d'invariance par translation.

La couche de pooling fonctionne indépendamment sur chaque tranche de profondeur de l'entrée et la redimensionne uniquement au niveau de la surface. La forme la plus courante est une couche de mise en commun avec des tuiles de taille 2 × 2 (largeur/hauteur) et comme valeur de sortie la valeur maximale en entrée (cf. schéma). On parle dans ce cas de « Max-Pool 2x2 » (compression d'un facteur 4).

Il est possible d'utiliser d'autres fonctions de pooling que le maximum. On peut utiliser un « average pooling » (la sortie est la moyenne des valeurs du patch d'entrée), du « L2-norm pooling ». Dans les faits, même si initialement l'average pooling était souvent utilisé il s'est avéré que le max-pooling était plus efficace car celui-ci augmente plus significativement l'importance des activations fortes. En d'autres circonstances, on pourra utiliser un pooling stochastique (voir « Méthodes de régularisation » plus bas dans ce document).

Le pooling permet de gros gains en puissance de calcul. Cependant, en raison de la réduction agressive de la taille de la représentation (et donc de la perte d'information associée), la tendance actuelle est d'utiliser de petits filtres[29] (type 2 × 2). Il est aussi possible d'éviter la couche de pooling[30] mais cela implique un risque de sur-apprentissage plus important.

Couches de correction (ReLU, sigmoïde, etc.)

Souvent, il est possible d'améliorer l'efficacité du traitement en intercalant entre les couches de traitement une couche qui va opérer une fonction mathématique (fonction d'activation) sur les signaux de sortie. On a notamment :

  • La correction ReLU (abréviation de Unité Linéaire Rectifiée) : . Cette fonction, appelée aussi fonction d'activation non saturante[réf. nécessaire], augmente les propriétés non linéaires de la fonction de décision et de l'ensemble du réseau sans affecter les champs récepteurs de la couche de convolution.
  • La correction par tangente hyperbolique ,
  • La correction par la tangente hyperbolique saturante : ,
  • La correction par la fonction sigmoïde .

Souvent, la correction ReLU est préférable, car il en résulte la formation de réseau neuronal plusieurs fois plus rapide[31], sans faire une différence significative à la généralisation de précision.

Couche entièrement connectée (FC)

Après plusieurs couches de convolution et de max-pooling, le raisonnement de haut niveau dans le réseau neuronal se fait via des couches entièrement connectées. Les neurones dans une couche entièrement connectée ont des connexions vers toutes les sorties de la couche précédente (comme on le voit régulièrement dans les réseaux réguliers de neurones). Leurs fonctions d'activations peuvent donc être calculées avec une multiplication matricielle suivie d'un décalage de polarisation.

Couche de perte (LOSS)

La couche de perte spécifie comment l'entrainement du réseau pénalise l'écart entre le signal prévu et réel. Elle est normalement la dernière couche dans le réseau. Diverses fonctions de perte adaptées à différentes tâches peuvent y être utilisées. La perte « Softmax »est utilisée pour prédire une seule classe parmi K classes mutuellement exclusives. La perte par entropie croisée sigmoïde est utilisée pour prédire K valeurs de probabilité indépendante dans . La perte euclidienne est utilisée pour régresser vers des valeurs réelles dans .

Exemples de modèles de CNN
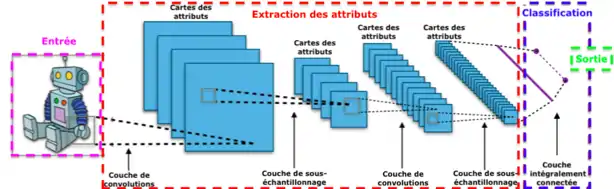
Architecture standard d'un réseau à convolutions.

La forme la plus commune d'une architecture de réseau de neurones convolutifs empile quelques couches Conv-ReLU, les suit avec des couches Pool, et répète ce schéma jusqu'à ce que l'entrée soit réduite dans un espace d'une taille suffisamment petite. À un moment, il est fréquent de placer des couches entièrement connectées (FC). La dernière couche entièrement connectée est reliée vers la sortie. Voici quelques architectures communes de réseau de neurones convolutifs qui suivent ce modèle :

  • INPUT -> FC implémente un classifieur linéaire
  • INPUT -> CONV -> RELU -> FC
  • INPUT -> [CONV -> RELU -> POOL] * 2 -> FC -> RELU -> FC Ici, il y a une couche de CONV unique entre chaque couche POOL
  • INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL] * 3 -> [FC -> RELU] * 2 -> FC Ici, il y a deux couches CONV empilées avant chaque couche POOL.

L'empilage des couches CONV avec de petits filtres de pooling permet un traitement plus puissant, avec moins de paramètres. Cependant, avec l’inconvénient de demander plus de puissance de calcul (pour contenir tous les résultats intermédiaires de la couche CONV).

Choix des hyperparamètres

Les réseaux de neurones convolutifs utilisent plus d'hyperparamètres qu'un perceptron multicouche standard. Même si les règles habituelles pour les taux d'apprentissage et des constantes de régularisation s'appliquent toujours, il faut prendre en considération les notions de nombre de filtres, leur forme et la forme du max pooling.

Nombre de filtres

Comme la taille des images intermédiaires diminue avec la profondeur du traitement, les couches proches de l'entrée ont tendance à avoir moins de filtres tandis que les couches plus proches de la sortie peuvent en avoir davantage. Pour égaliser le calcul à chaque couche, le produit du nombre de caractéristiques et le nombre de pixels traités est généralement choisi pour être à peu près constant à travers les couches. Pour préserver l'information en entrée, il faudrait maintenir le nombre de sorties intermédiaires (nombre d'images intermédiaires multiplié par le nombre de positions de pixel) pour être croissante (au sens large) d'une couche à l'autre.

Le nombre d'images intermédiaires contrôle directement la puissance du système, dépend du nombre d'exemples disponibles et la complexité du traitement.

Forme du filtre

Les formes de filtre varient grandement dans la littérature. Ils sont généralement choisis en fonction de l'ensemble de données. Les meilleurs résultats sur les images de MNIST (28 x 28) sont habituellement dans la gamme de 5 × 5 sur la première couche, tandis que les ensembles de données d'images naturelles (souvent avec des centaines de pixels dans chaque dimension) ont tendance à utiliser de plus grands filtres de première couche de 12 × 12, voire 15 × 15.

Le défi est donc de trouver le bon niveau de granularité de manière à créer des abstractions à l'échelle appropriée et adaptée à chaque cas.

Forme du Max Pooling

Les valeurs typiques sont 2 × 2. De très grands volumes d'entrée peuvent justifier un pooling 4 × 4 dans les premières couches. Cependant, le choix de formes plus grandes va considérablement réduire la dimension du signal, et peut entraîner la perte de trop d'information.

Méthodes de régularisation

En apprentissage automatique, la régularisation est un procédé visant à améliorer les performances de généralisation d'un algorithme d'apprentissage, autrement dit à diminuer son erreur sur échantillons de test. Cela peut éventuellement être réalisé au détriment de l'erreur d'apprentissage. Un tel procédé a pour but d'éviter le sur-apprentissage qui résulte d'une adaptation trop forte du modèle aux données d'entraînement. Du point de vue du compromis biais/variance, le sur-apprentissage décrit un modèle capable de très bien s'adapter à tout ensemble d'apprentissage donné (faible biais) mais devrait fortement modifier ses paramètres (poids) pour s'adapter à un autre jeu de données d'apprentissage (forte variance)[32].

Dropout

La méthode du dropout[33] consiste à « désactiver » des sorties de neurones aléatoirement (avec une probabilité prédéfinie, par exemple 0.5 pour les couches cachées et 0.8 pour la couche d'entrée) pendant la phase d'apprentissage. Cela revient à simuler un ensemble de modèles différents (bagging) et à les apprendre conjointement (bien qu'aucun ne soit appris de bout en bout). Chaque neurone étant possiblement inactif pendant une itération d'apprentissage, cela force chaque unité à « bien apprendre » indépendamment des autres et évite ainsi la « co-adaptation »[32]. Le dropout peut permettre une accélération de l'apprentissage.

En phase de test, les auteurs proposent de pondérer chaque poids appris par sa probabilité d'activation pendant l'apprentissage. Pour un dropout avec un probabilité 0.5 par exemple, cela revient à diviser les poids par deux[32].

La technique du dropout est notamment utilisée dans les systèmes de reconnaissance d'image, de voix, le classement de documents et sur des problèmes de calculs en biologie.

DropConnect

Le DropConnect[34] est une alternative au dropout consistant à inhiber une connexion (l'équivalent de la synapse), et ce de manière toujours aléatoire. Les résultats sont similaires (rapidité, capacité de généralisation de l'apprentissage) au dropout, mais présentent une différence au niveau de l'évolution des poids des connexions. Une couche « complètement connectée » avec un DropConnect peut s'apparenter à une couche à connexion « diffuse ».

Pooling stochastique

Le pooling stochastique[35] reprend le même principe que le Max-pooling, mais la sortie choisie sera prise au hasard, selon une distribution multinomiale définie en fonction de l'activité de la zone adressée par le pool.

Dans les faits, ce système s'apparente à faire du Max-pooling avec un grand nombre d'images similaires, qui ne varient que par des déformations localisées. On peut aussi considérer cette méthode comme une adaptation à des déformations élastiques de l'image[36]. C'est pourquoi cette méthode est très efficace sur les images MNIST (base de données d'images représentant des chiffres manuscrits). La force du pooling stochastique est de voir ses performances croître de manière exponentielle avec le nombre de couches du réseau.

Données artificielles

Pour limiter le sur-apprentissage (sur-rigidité du réseau de neurones), il est possible de légèrement modifier les données en entrée à partir des données déjà existantes. On va par exemple déformer légèrement une image ou la redimensionner pour recréer une nouvelle image d'entraînement. Il peut être possible aussi de créer des données complètement artificielles. Le but est d'augmenter le nombre de données d'entraînement (souvent des images) pour améliorer les performances du réseau[37].

Taille du réseau

La manière la plus simple de limiter le surapprentissage (problèmes de convergence du traitement) est de limiter le nombre de couches du réseau et de libérer les paramètres libres (connexions) du réseau. Ceci réduit directement la puissance et le potentiel prédictif du réseau. C'est équivalent à avoir une « norme zéro ».

Dégradation du poids

Le concept est de considérer le vecteur des poids d'un neurone (liste des poids associés aux signaux entrants), et de lui rajouter un vecteur d'erreur proportionnel à la somme des poids (norme 1) ou du carré des poids (norme 2 ou euclidienne). Ce vecteur d'erreur peut ensuite être multiplié par un coefficient de proportionnalité que l'on va augmenter pour pénaliser davantage les vecteurs de poids forts.

  • La régularisation par norme 1 : La spécificité de cette régulation est de diminuer le poids des entrées aléatoires et faibles et d'augmenter le poids des entrées « importantes ». Le système devient moins sensible au bruit.
  • La régularisation par norme 2 : (norme euclidienne) La spécificité de cette régulation est de diminuer le poids des entrées fortes, et de forcer le neurone à plus prendre en compte les entrées de poids faible.

Les régularisations par norme 1 et norme 2 peuvent être combinées : c'est la « régularisation de réseau élastique » (Elastic net regulation)[réf. souhaitée].

La limitation du vecteur de poids

Certaines publications[38] montrent qu'il peut être utile de limiter la norme du vecteur de poids des neurones : . Dans les faits, le vecteur de poids est ajusté de manière habituelle, puis il est écrêté selon l'algorithme du gradient projeté, pour atteindre la norme désirée.

Recadrage intelligent

Si le pooling permet d'augmenter l'efficacité du traitement, il détruit le lien entre une image et son contenu (ex. le nez et le visage). Cette relation peut être pourtant très utile (notamment en reconnaissance faciale). En faisant déborder les tuiles de pooling les unes sur les autres, il est possible de définir une position pour un élément (ex. le nez est toujours au milieu du visage), mais ce débordement par translation empêche toute autre forme d'extrapolation (changement d'angle de vue, d'échelle…), contrairement à ce que le cerveau humain est capable de faire[39].

À ce jour, cette limitation est contournée en modifiant légèrement les images d'entraînement (luminosité, angle, taille…), mais au prix d'un coûteux temps d'apprentissage. Il est cependant possible d'utiliser un pavage intelligent : l'image globale est analysée et lorsqu'un élément est identifié, il est extrait de l'image (recadré), puis envoyé vers la couche suivante. C'est un fonctionnement utile pour reconnaître les individus d'une photo. Le premier étage de traitement identifie les visages tandis que le second essaye d'identifier la personne qui correspond à ce visage (cf. identification automatique dans les photos publiées sur Facebook). On peut comparer ce fonctionnement à une focalisation du regard. Lorsqu'on veut reconnaître une personne qui passe, on la regarde dans les yeux (recadrage)[40].

De plus, il devient possible de prédire la présence d'un élément grâce à la vision d'un ensemble de ses sous-parties (si je vois deux yeux et un nez, il y a de fortes chances pour que je sois face à un visage, même si je ne le vois pas complètement). Il est possible d'ajuster la taille et la position du recadrage (opérations linéaires) pour faciliter et généraliser le traitement[41].

Notes et références
  1. (en) « Convolutional Neural Networks (LeNet) – DeepLearning 0.1 documentation », sur DeepLearning 0.1, LISA Lab (consulté le ).
  2. (en) Masakazu Matusugu, Katsuhiko Mori, Yusuke Mitari et Yuji Kaneda, « Subject independent facial expression recognition with robust face detection using a convolutional neural network », Neural Networks, vol. 16, no 5,‎ , p. 555–559 (DOI 10.1016/S0893-6080(03)00115-1, lire en ligne, consulté le ).
  3. (en) Yann LeCun, « LeNet-5, convolutional neural networks » (consulté le ).
  4. (en) Aaron van den Oord, Sander Dieleman, Benjamin Schrauwen, C. J. C. Burges, L. Bottou, M. Welling, Z. Ghahramani et K. Q. Weinberger, Deep content-based music recommendation, Curran Associates, Inc., , 2643–2651 p. (lire en ligne).
  5. (en) Ronan Collobert et Jason Weston, « A Unified Architecture for Natural Language Processing: Deep Neural Networks with Multitask Learning », Proceedings of the 25th International Conference on Machine Learning, New York, NY, USA, ACM, iCML '08,‎ , p. 160–167 (ISBN 978-1-60558-205-4, DOI 10.1145/1390156.1390177, lire en ligne).
  6. (en) Dan Ciresan, Üli Meier et Jürgen Schmidhuber, « Multi-column deep neural networks for image classification », Conference on Computer Vision and Pattern Recognition 2012, New York, NY, Institute of Electrical and Electronics Engineers (IEEE),‎ , p. 3642–3649 (ISBN 978-1-4673-1226-4, OCLC 812295155, DOI 10.1109/CVPR.2012.6248110, arXiv 1202.2745v1, lire en ligne, consulté le ).
  7. (en) Dan Ciresan, Üli Meier, Jonathan Masci, Luca M. Gambardella et Jurgen Schmidhuber, « Flexible, High Performance Convolutional Neural Networks for Image Classification », Proceedings of the Twenty-Second international joint conference on Artificial Intelligence-Volume Volume Two, vol. 2,‎ , p. 1237–1242 (lire en ligne, consulté le ).
  8. (en) Alex Krizhevsky, « ImageNet Classification with Deep Convolutional Neural Networks » (consulté le ).
  9. (en) Keisuke Korekado, Takashi Morie, Osamu Nomura, Hiroshi Ando, Teppei Nakano, Masakazu Matsugu et Atsushi Iwata, « A Convolutional Neural Network VLSI for Image Recognition Using Merged/Mixed Analog-Digital Architecture », Knowledge-Based Intelligent Information and Engineering Systems,‎ , p. 169–176.
  10. (en) Patrick Le Callet, Christian Viard-Gaudin et Dominique Barba, « A Convolutional Neural Network Approach for Objective Video Quality Assessment », IEEE Transactions on Neural Networks, vol. 17, no 5,‎ , p. 1316–1327 (PMID 17001990, DOI 10.1109/TNN.2006.879766, lire en ligne, consulté le ).
  11. (en) D. H. Hubel et T. N. Wiesel, « Receptive fields and functional architecture of monkey striate cortex », The Journal of Physiology, vol. 195, no 1,‎ , p. 215–243 (ISSN 0022-3751, PMID 4966457, PMCID 1557912, lire en ligne).
  12. (en) Yann LeCun, Yoshua Bengio et Geoffrey Hinton, « Deep learning », Nature, vol. 521, no 7553,‎ , p. 436–444 (PMID 26017442, DOI 10.1038/nature14539).
  13. (en) Kunihiko Fukushima, « Neocognitron: A Self-organizing Neural Network Model for a Mechanism of Pattern Recognition Unaffected by Shift in Position », Biological Cybernetics, vol. 36, no 4,‎ , p. 193–202 (PMID 737036, DOI 10.1007/BF00344251, lire en ligne, consulté le ).
  14. (en) Toshiteru Homma, Les Atlas et Robert II Marks, « An Artificial Neural Network for Spatio-Temporal Bipolar Patters: Application to Phoneme Classification », Advances in Neural Information Processing Systems, vol. 1,‎ , p. 31–40 (lire en ligne)
  15. (en) Yann LeCun, Léon Bottou, Yoshua Bengio et Patrick Haffner, « Gradient-based learning applied to document recognition », Proceedings of the IEEE, vol. 86, no 11,‎ , p. 2278–2324 (DOI 10.1109/5.726791, lire en ligne, consulté le ).
  16. (en) S. Behnke., « Hierarchical Neural Networks for Image Interpretation », Lecture Notes in Computer Science, Springer, vol. 2766,‎ .
  17. (en) Patrice Simard, David Steinkraus et John C. Platt, « Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis », ICDAR, vol. 3,‎ , p. 958–962.
  18. (en) Daniel Graupe, Ruey Wen Liu et George S Moschytz, « Applications of neural networks to medical signal processing », Proc. 27th IEEE Decision and Control Conf.,‎ , p. 343–347.
  19. (en) Daniel Graupe, Boris Vern, G. Gruener, Aaron Field et Qiu Huang, « Decomposition of surface EMG signals into single fiber action potentials by means of neural network », Proc. 27th IEEE Decision and Control Conf.,‎ , p. 1008–1011.
  20. (en) Qiu Huang, Daniel Graupe, Yi Fang Huang et Ruey Wen Liu, « Identification of firing patterns of neuronal signals », Proc. 28th IEEE Decision and Control Conf.,‎ 1989., p. 266–271.
  21. (en) Dave Steinkraus, Ian Buck et Patrice Simard, 12th International Conference on Document Analysis and Recognition (ICDAR 2005), , 1115–1119 p. (lire en ligne), « Using GPUs for Machine Learning Algorithms ».
  22. (en) Kumar Chellapilla (dir.), Sid Puri et Patrice Simard, Tenth International Workshop on Frontiers in Handwriting Recognition, Suvisoft, (lire en ligne), « High Performance Convolutional Neural Networks for Document Processing ».
  23. (en) G. E. Hinton, S. Osindero et Y. W. Teh, « A fast learning algorithm for deep belief nets », Neural Computation, vol. 18, no 7,‎ , p. 1527–1554 (PMID 16764513, DOI 10.1162/neco.2006.18.7.1527).
  24. (en) Yoshua Bengio, Pascal Lamblin, Dan Popovici et Hugo Larochelle, « Greedy Layer-Wise Training of Deep Networks », Advances in Neural Information Processing Systems,‎ , p. 153–160.
  25. (en) MarcAurelio Ranzato, Christopher Poultney, Sumit Chopra et Yann LeCun, « Efficient Learning of Sparse Representations with an Energy-Based Model », Advances in Neural Information Processing Systems,‎ (lire en ligne).
  26. (en) Deng, Jia et al., « Imagenet: A large-scale hierarchical image database », IEEE Conference on Computer Vision and Pattern Recognition 2009,‎ .
  27. Emilie Poisson et Christian Viard-Gaudin, « Réseaux de neurones à convolution - Reconnaissance de l’écriture manuscrite non contrainte », sur http://emilie.caillault.free.fr/, (consulté le ).
  28. (en) Ian J. Goodfellow, Yoshua Bengio et Aaron Courville, Deep Learning, MIT Press, (ISBN 0262035618, lire en ligne) [détail des éditions], chapitre 9.
  29. (en) Benjamin Graham « Fractional Max-Pooling », ..
  30. (en) Jost Tobias Springenberg, Alexey Dosovitskiy, Thomas Brox et Martin Riedmiller « Striving for Simplicity: The All Convolutional Net », ..
  31. (en) A. Krizhevsky, I. Sutskever et G. E. Hinton, « ImageNet Classification with Deep Convolutional Neural Networks », Advances in neural Processing Systems de traitement, vol. 1,‎ , p. 1097–1105 (lire en ligne [archive du ]).
  32. (en) Ian J. Goodfellow, Yoshua Bengio et Aaron Courville, Deep Learning, MIT Press, (ISBN 0262035618, lire en ligne) [détail des éditions], chapitre 7.
  33. (en) Nitish Srivastava, C. Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever et Ruslan Salakhutdinov, « Dropout: A Simple Way to Prevent Neural Networks from overfitting », Journal of Machine Learning Research, vol. 15, no 1,‎ , p. 1929–1958 (lire en ligne [PDF]).
  34. (en) « Regularization of Neural Networks using DropConnect | ICML 2013 | JMLR W&CP », sur jmlr.org (consulté le ).
  35. (en) Auteur inconnu « Stochastic Pooling for Regularization of Deep Convolutional Neural Networks », ..
  36. (en) « Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis – Microsoft Research », sur research.microsoft.com (consulté le ).
  37. (en) Geoffrey E. Hinton, Nitish Srivastava, Alex Krizhevsky, Ilya Sutskever et Ruslan R. Salakhutdinov « Improving neural networks by preventing co-adaptation of feature detectors », ..
  38. (en) « Dropout: A Simple Way to Prevent Neural Networks from Overfitting », sur jmlr.org (consulté le ).
  39. Hinton, Geoffrey. « Some demonstrations of the effects of structural descriptions in mental imagery.» Cognitive Science 3.3 (1979): 231-250.
  40. Rock, Irvin. « The frame of reference.» The legacy of Solomon Asch: Essays in cognition and social psychology (1990): 243-268.
  41. J. Hinton, Coursera lectures on Neural Networks, 2012, Url: https://www.coursera.org/course/neuralnets?

Voir aussi

Liens externes

Bibliographie

(en) Ian J. Goodfellow, Yoshua Bengio et Aaron Courville, Deep Learning, MIT Press, (ISBN 0262035618, lire en ligne) [détail des éditions]


  • Portail des neurosciences
  • Portail des probabilités et de la statistique
  • Portail de l'informatique théorique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.