Rosette de Klemperer
Une rosette de Klemperer est un système gravitationnel composé de deux types de corps célestes (un type étant plus lourd que l'autre) qui orbitent autour d'un barycentre selon le même motif. Wolfgang Klemperer est le premier à décrire ce système en 1962[1].
Description
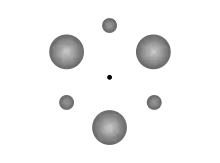
La rosette la plus simple est composée de quatre corps célestes qui occupent les quatre coins d'un losange [lourd, léger, lourd, léger], les plus lourds étant de même masse, les plus légers étant de même masse. Une rosette peut comprendre plusieurs types de masses, du moment qu'elles forment un motif cyclique (par exemple, [ 1,2,3 ... 1,2,3 ], [ 1,2,3,4,5 ... 1,2,3,4,5 ] ou [ 1,2,3,3,2,1 ... 1,2,3,3,2,1]). Dans son article, Klemperer discute de rosettes octogonale et rhombique. À l'exception d'une seule, toutes les rosettes sont instables. La rosette hexagonale du schéma à la droite démontre une grande stabilité parce que les corps célestes se trouvent aux points de Lagrange L4 et L5 des corps célestes voisins.
Usage erroné
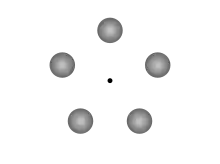
Le terme « rosette de Klemperer » (souvent écrit « rosette de Kemplerer », ce qui est fautif) est régulièrement utilisé pour désigner un arrangement régulier de trois corps célestes ou plus d'une même masse (polygone régulier), et animés de la même vitesse angulaire autour du barycentre. Klemperer connaît cette configuration stable, qu'il mentionne dès le début de son article, mais poursuit avec la description des rosettes.
Dans le roman L'Anneau-Monde de Larry Niven, les mondes des Marionnettistes de Pierson sont arrangés ainsi (5 planètes également distantes formant un pentagone). Niven appelle cet arrangement « rosette de Kemplerer » ; cette faute d'épellation (peut-être volontaire) est une source de cette confusion. Une autre source de confusion provient de la ressemblance du nom de Klemperer et de Johannes Kepler, à qui l'on doit des lois du mouvement planétaire.
Instabilité
Des simulations ont démontré que ces systèmes sont instables[2] : n'importe quel déplacement qui éloigne un corps céleste de la configuration géométrique idéale provoque une oscillation, ce qui disloque l'arrangement (l'article de Klemperer discute ce scénario), peu importe que le centre de la rosette se trouve dans un espace vide ou que les corps orbitent autour d'une étoile.
Deux types de perturbations peuvent rendre instables une rosette de Klemperer. Une perturbation tangentielle amène un corps plus proche d'un second, ce rapprochement étant suivi d'un autre parce que ce corps céleste subit moins d'attraction gravitationnelle de ses autres voisins et plus du second. Une perturbation radiale force les corps célestes à tous se rapprocher les uns des autres, augmentant leur vitesse orbitale, ce qui se traduit par une perturbation tangentielle.
Notes et références
(en) Cet article est partiellement ou en totalité issu de la page de Wikipédia en anglais intitulée « Klemperer rosette » (voir la liste des auteurs).
- (en) W. B. Klemperer, « Some Properties of Rosette Configurations of Gravitating Bodies in Homographic Equilibrium », The Astronomical Journal, vol. 67, no 3, , p. 162–7 (DOI 10.1086/108686, Bibcode 1962AJ.....67..162K)
- (en) Bob Jenkins, « Klemperer Rosettes » (consulté le )
Liens externes
- (en) Simulations avec applets Java
- (en) Kemplerer (Klemperer) Rosette de Larry Niven, auteur de Ringworld
- Portail de l’astronomie