Snark double étoile

Le snark double étoile est, en théorie des graphes, un graphe 3-régulier possédant 30 sommets et 45 arêtes.

Snark double étoile

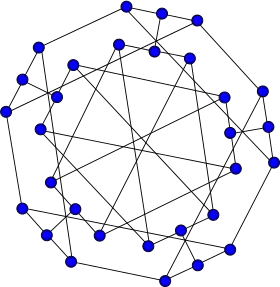Représentation du snark double étoile
Nombre de sommets 30
Nombre d'arêtes 45
Distribution des degrés 3-régulier
Rayon 4
Diamètre 4
Maille 6
Automorphismes 80
Nombre chromatique 3
Indice chromatique 4
Propriétés Régulier
Snark
Hypohamiltonien

En 1975, Isaacs introduit deux familles infinies de snarks, les deux premières découvertes : les snarks fleurs et les snarks BDS, une famille qui comprend tous les snarks jusqu'alors connus : le graphe de Petersen, le premier snark de Blanuša, le second snark de Blanuša, le snark de Descartes et le snark de Szekeres (BDS est l'abréviation pour Blanuša Descartes Szekeres)[1]. Isaacs découvre au passage une snark à 30 sommets qui n'appartient pas à la famille BSD et qui n'est pas non plus un snark fleur. Il le nomme le snark double étoile.

Propriétés

Propriétés générales

Le diamètre du snark double étoile, l'excentricité maximale de ses sommets, est 4, son rayon, l'excentricité minimale de ses sommets, est 4 et sa maille, la longueur de son plus court cycle, est 6. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes.

Coloration

Le nombre chromatique du snark double étoile est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes mais ce nombre est minimal. Il n'existe pas de 2-coloration valide du graphe.

L'indice chromatique du snark double étoile est 4. Il existe donc une 4-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.

Propriétés algébriques

Le groupe d'automorphismes du snark double étoile est un groupe d'ordre 80.

Le polynôme caractéristique de la matrice d'adjacence du snark double étoile est : .

Voir aussi

Liens internes

Liens externes

Références
  1. (en) R. Isaacs, « Infinite families of non-trivial trivalent graphs which are not Tait-colorable », American Mathematical Monthly, vol. 82,‎ , p. 221–239 (DOI 10.2307/2319844)
  • Portail des mathématiques
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.