Théorème de Fleischner
En théorie des graphes, le théorème de Fleischner donne une condition suffisante pour qu'un graphe contienne un cycle hamiltonien. Il dit que le carré (en) d'un graphe biconnexe est un graphe hamiltonien. Le théorème porte le nom de Herbert Fleischner, qui en a publié la preuve en 1974.
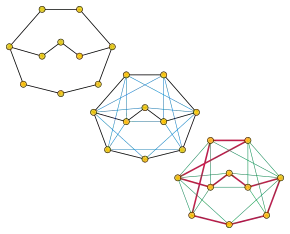
Définitions et énoncé
Un graphe non orienté G est hamiltonien s'il contient un cycle qui passe par chacun de ses sommets exactement une fois. Il est 2-connexe (ou biconnexe) s'il ne possède pas de point d'articulation, un sommet dont la suppression déconnecte le graphe. Tous les graphes biconnexes ne sont pas hamiltoniens : des contre-exemples sont par exemple le graphe de Petersen et le graphe biparti complet K 2,3 .
Le carré de G est un graphe G 2 qui a le même ensemble de sommets que G, et dans lequel deux sommets sont adjacents si et seulement s'ils ont une distance d'au plus deux dans G. Le théorème de Fleischner est :
Théorème de Fleischner — Le carré d'un graphe fini biconnexe avec au moins trois sommets est hamiltonien.
De manière équivalente, les sommets de chaque graphe biconnexe G peuvent être ordonnés cycliquement de telle sorte que les sommets adjacents dans cet ordre soient à une distance d'au plus deux les uns des autres dans G.
Extensions
Dans le théorème de Fleischner, on peut contraindre le cycle hamiltonien de G 2 à ce que pour deux sommets donnés v et w de G il contienne deux arêtes de G incidentes à v et une arête de G incidente à w . De plus, si v et w sont adjacents dans G, alors ce sont trois arêtes différentes de G[1].
En plus d'avoir un cycle hamiltonien, le carré d'un graphe G biconnexe est également connexe au sens hamiltonien (ce qui signifie qu'il possède chemin hamiltonien commençant et se terminant en deux sommets spécifiés) et être 1-hamiltonien (ce qui signifie que si un sommet est supprimé, le graphe restant possède encore un cycle hamiltonien)[2] . Il est également un graphe pancyclique, ce qui signifie que pour chaque sommet v et tout entier k avec , il existe un cycle de longueur k contenant v[3].
Si un graphe G n'est pas biconnexe, alors son carré peut ou non avoir un cycle hamiltonien, et déterminer s'il en a un est NP-complet[4].
Un graphe infini ne peut pas avoir un cycle hamiltonien, car chaque cycle est fini, mais Carsten Thomassen a prouvé que si G est un graphe biconnexe localement fini avec une seule bout, alors G 2 a un chemin hamiltonien doublement infini[5]. Plus généralement, si G est localement fini, biconnex et a un nombre quelconque de bouts, alors G 2 a un cercle hamiltonien. Dans un espace topologique compact obtenu en considérant le graphe comme un complexe simplicial et en ajoutant un point supplémentaire à l'infini à chacune de ses bouts, un cercle hamiltonien est défini comme un sous-espace homéomorphe à un cercle euclidien qui couvre chaque sommet.
Algorithmes
Le cycle hamiltonien dans carré d'un graphe biconnexe à n sommet peut être trouvé en temps linéaire[6], ce résultat datant de 2018 améliore la première solution algorithmique de Lau en temps d'exécution O (n 2 )[7]. Le théorème de Fleischner peut être utilisé pour fournir une 2-approximation du problème de goulot d'étranglement du voyageur de commerce dans les espaces métriques[8].
Historique
Une preuve du théorème de Fleischner a été annoncée par Herbert Fleischner en 1971 et publiée par lui en 1974, résolvant ainsi une conjecture de 1966 de Crispin Nash-Williams, énoncée également indépendamment par L. W. Beineke et Michael D. Plummer[9]. Dans son compte-rendu de l'article de Fleischner, Nash-Williams écrit que celui-ci avait résolu « un problème bien connu qui a résisté pendant plusieurs années l'ingéniosité d'autres théoriciens des graphes »[10]
La preuve originale de Fleischner était compliquée. Václav Chvátal, dans l'article où il introduit la ténacité graphique, observe que le carré d'un graphe k-sommet-connexe est nécessairement k-dur; il conjectura que les graphes 2-durs sont hamiltoniens, ce qui aurait donné une autre preuve du théorème de Fleischner[11]. Des contre-exemples à cette conjecture ont été découverts plus tard, [12] mais la possibilité qu'une borne finie sur la dureté pourrait impliquer le caractère hamiltonien reste un problème ouvert important dans la théorie des graphes. Une preuve plus simple, à la fois du théorème de Fleischner et de ses extensions par [13], a été donnée par (Říha 1991)[14], et une autre démonstration simplifiée du théorème a été donnée par Georgakopoulos en 2009[15]'[16]'[17].
Notes et références
Notes
- (Fleischner 1976); (Müttel et Rautenbach 2012).
- (Chartrand et al. 1974); (Chartrand, Lesniak et Zhang 2010)
- (Hobbs 1976), en réponse à une conjecture de (Bondy 1971).
- (Underground 1978); (Bondy 1995).
- Thomassen (1978).
- (Alstrup, Georgakopoulos, Rotenberg, Thomassen 2018)
- (Lau 1980); (Parker et Rardin 1984).
- (Parker et Rardin 1984); (Hochbaum et Shmoys 1986).
- (Fleischner 1974). Pour des conjectures antérieures, voir Fleischner and (Chartrand, Lesniak et Zhang 2010).
- Compte-rendu sur MathReviews : lien Math Reviews
- (Chvátal 1973); (Bondy 1995).
- Bauer, Broersma et Veldman (2000).
- Chartrand et al. (1974).
- (Bondy 1995); (Chartrand, Lesniak et Zhang 2010).
- Georgakopoulos (2009a).
- Chartrand, Lesniak et Zhang (2010).
- Diestel (2012).
Articles
- Stephen Alstrup, Agelos Georgakopoulos, Eva Rotenberg et Carsten Thomassen, « A Hamiltonian Cycle in the Square of a 2-connected Graph in Linear Time », Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms, , p. 1645–1649 (ISBN 978-1-61197-503-1, DOI 10.1137/1.9781611975031.107)
- D. Bauer, H. J. Broersma et H. J. Veldman, « Not every 2-tough graph is Hamiltonian », Discrete Applied Mathematics, vol. 99, nos 1–3, , p. 317–321 (DOI 10.1016/S0166-218X(99)00141-9, Math Reviews 1743840, lire en ligne).
- J. A. Bondy, « Pancyclic graphs », Proceedings of the Second Louisiana Conference on Combinatorics, Graph Theory and Computing (Louisiana State Univ., Baton Rouge, La., 1971), Baton Rouge, Louisiana, Louisiana State University, , p. 167–172 (Math Reviews 0325458).
- G. Chartrand, Arthur M. Hobbs, H. A. Jung, S. F. Kapoor et C. St. J. A. Nash-Williams, « The square of a block is Hamiltonian connected », Journal of Combinatorial Theory B, vol. 16, no 3, , p. 290–292 (DOI 10.1016/0095-8956(74)90075-6, Math Reviews 0345865).
- Václav Chvátal, « Tough graphs and Hamiltonian circuits », Discrete Mathematics, vol. 5, no 3, , p. 215–228 (DOI 10.1016/0012-365X(73)90138-6, Math Reviews 0316301).
- Herbert Fleischner, « The square of every two-connected graph is Hamiltonian », Journal of Combinatorial Theory B, vol. 16, , p. 29–34 (DOI 10.1016/0095-8956(74)90091-4, Math Reviews 0332573).
- Herbert Fleischner, « In the square of graphs, Hamiltonicity and pancyclicity, Hamiltonian connectedness and panconnectedness are equivalent concepts », Monatshefte für Mathematik, vol. 82, no 2, , p. 125–149 (DOI 10.1007/BF01305995, Math Reviews 0427135).
- Agelos Georgakopoulos, « A short proof of Fleischner's theorem », Discrete Mathematics, vol. 309, nos 23–24, 2009a, p. 6632–6634 (DOI 10.1016/j.disc.2009.06.024, Math Reviews 2558627).
- Agelos Georgakopoulos, « Infinite Hamilton cycles in squares of locally finite graphs », Advances in Mathematics, vol. 220, no 3, 2009b, p. 670–705 (DOI 10.1016/j.aim.2008.09.014, Math Reviews 2483226).
- Arthur M. Hobbs, « The square of a block is vertex pancyclic », Journal of Combinatorial Theory, vol. 20, no 1, , p. 1–4 (DOI 10.1016/0095-8956(76)90061-7, Math Reviews 0416980).
- Dorit S. Hochbaum et David B. Shmoys, « A unified approach to approximation algorithms for bottleneck problems », Journal of the ACM, New York, NY, USA, ACM, vol. 33, no 3, , p. 533–550 (DOI 10.1145/5925.5933, lire en ligne).
- H. T. Lau (Ph.D. thesis), Finding a Hamiltonian cycle in the square of a block., Montreal, McGill University, . Cité par (Hochbaum et Shmoys 1986).
- Janina Müttel et Dieter Rautenbach, « A short proof of the versatile version of Fleischner's theorem », Discrete Mathematics, vol. 313, no 19, , p. 1929–1933 (DOI 10.1016/j.disc.2012.07.032).
- R. Garey Parker et Ronald L. Rardin, « Guaranteed performance heuristics for the bottleneck traveling salesman problem », Operations Research Letters, vol. 2, no 6, , p. 269–272 (DOI 10.1016/0167-6377(84)90077-4).
- Stanislav Říha, « A new proof of the theorem by Fleischner », Journal of Combinatorial Theory, vol. 52, no 1, , p. 117–123 (DOI 10.1016/0095-8956(91)90098-5, Math Reviews 1109427).
- Carsten Thomassen, « Hamiltonian paths in squares of infinite locally finite blocks », Advances in Graph Theory (Cambridge Combinatorial Conf., Trinity College, Cambridge, 1977), Elsevier, vol. 3, , 269–277 (ISBN 978-0-7204-0843-0, DOI 10.1016/S0167-5060(08)70512-0, Math Reviews 499125, lire en ligne).
- Polly Underground, « On graphs with Hamiltonian squares », Discrete Mathematics, vol. 21, no 3, , p. 323 (DOI 10.1016/0012-365X(78)90164-4, Math Reviews 522906).
Ouvrages généraux
- J. A. Bondy, Handbook of combinatorics, Vol. 1, 2, Amsterdam, Elsevier, (Math Reviews 1373656), « Basic graph theory: paths and circuits », p. 3–110.
- Gary Chartrand, Linda Lesniak et Ping Zhang, Graphs & Digraphs, CRC Press, , 5e éd. (ISBN 9781439826270, lire en ligne), p. 139.
- Reinhard Diestel, Graph Theory, , 4e éd. (lire en ligne), « 10. Hamiltonian cycles »
- Portail des mathématiques
- Portail de l'informatique théorique