Graphe pancyclique

Un graphe ${\displaystyle G}$ à ${\displaystyle n}$ sommets est pancyclique si, pour tout entier ${\displaystyle k}$ avec ${\displaystyle 3\leq k\leq n}$, le graphe contient un cycle de longueur ${\displaystyle k}$[1]. Il est nœud-pancyclique ou sommet-pancyclique si, pour chaque sommet ${\displaystyle s}$ et tout ${\displaystyle k}$ avec ${\displaystyle 3\leq k\leq n}$, il contient un cycle de longueur ${\displaystyle k}$ qui passe par ${\displaystyle s}$[2]. De même, il est arête-pancyclique si, pour chaque arête ${\displaystyle a}$ et tout ${\displaystyle k}$, il contient un cycle de longueur ${\displaystyle k}$ qui utilise ${\displaystyle a}$[2].

Un graphe biparti ne peut pas être pancyclique, car il ne contient aucun cycle de longueur impaire, mais il est dit bipancyclique s'il contient des cycles de toutes les longueurs paires de 4 à n[3].

Le nombre de graphes pancycliques à ${\displaystyle n=0,1,\ldots }$ sommets est 0, 0, 1, 2, 7, 43, 372, 6132, 176797, 9302828, ... (suite A286684 de l'OEIS).

Un graphe planaire extérieur maximal est par définition un graphe formé par un polygone simple du plan en triangulant son intérieur. Un graphe planaire extérieur maximal est pancyclique, comme on peut le montrer par induction. La face externe du graphe est un cycle de longueur n, et la suppression d'un triangle connecté au reste du graphe par une seule arête (une feuille de l'arbre qui forme le graphe dual de la triangulation) forme un graphe planaire extérieur maximal sur un sommet de moins, graphe qui par induction a des cycles de toutes les longueurs restantes. En choisissant convenablement le triangle à supprimer, le même argument montre en plus qu'un graphe planaire extérieur maximal est nœud-pancyclique[4]. Il en est de même pour les graphes qui ont un sous-graphe couvrant planaire extérieur maximal, comme c'est le cas par exemple pour les graphes roue.

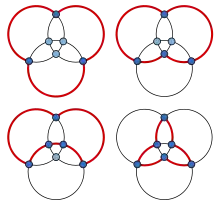
Un graphe planaire maximal est un graphe planaire dans lequel toutes les faces, même la face extérieure, sont des triangles. Un graphe planaire maximal est nœud-pancyclique si et seulement s'il a un cycle hamiltonien[5] en effet : s'il n'est pas hamiltonien, il n'est certainement pas pancyclique, et s'il est hamiltonien, alors l'intérieur du cycle hamiltonien forme un graphe planaire extérieur maximal sur les mêmes nœuds, auquel l'argument précédent pour les graphes planaires extérieurs maximaux s'applique[6]. Par exemple, l'illustration montre la pancyclicité du graphe d'un octaèdre, un graphe planaire maximal hamiltonien à six sommets. Par le même argument, si un graphe planaire maximal a un cycle de longueur k, il a des cycles de toutes les longueurs plus petites[7].

Un graphe de Halin presque pancyclique, avec des cycles de toutes longueurs jusqu'à n sauf de longueur 8.

Les graphes de Halin sont les graphes planaires formés à partir d'une représentation planaire d'un arbre qui n'a pas de sommet de degré deux, en ajoutant un cycle qui relie toutes les feuilles de l'arbre. Les graphes de Halin ne sont pas nécessairement pancycliques, mais ils sont presque pancycliques en ce sens qu'il manque au plus une longueur de cycle. La longueur du cycle manquant est nécessairement paire. Si aucun des sommets intérieurs d'un graphe de Halin n'a de degré trois, alors il est nécessairement pancyclique[8].

Bondy (1971) a observé que de nombreuses conditions usuelles pour l'existence d'un cycle hamiltonien étaient également des conditions suffisantes pour qu'un graphe soit pancyclique, et sur cette base il a conjecturé que tout graphe planaire à 4-connexe est pancyclique. Malkevitch (1971) a trouvé une famille de contre-exemples.

Un tournoi est un graphe orienté avec un arc entre chaque paire de sommets. Intuitivement, un tournoi peut être utilisé pour modéliser un tournoi toutes rondes, en traçant un arc du gagnant vers le perdant dans chaque match de la compétition. Un tournoi est dit fortement connexe ou fort si et seulement s'il ne peut pas être partitionné en deux sous-ensembles non vides P et G de perdants et de gagnants, tels que chaque concurrent de G bat chaque concurrent de P[9]. Un tournoi fort est pancyclique[10] et nœud-pancyclique[11]. Si un tournoi est régulier (chaque concurrent a le même nombre de victoires et de défaites que chaque autre concurrent), alors il est également pancyclique[12] ; cependant, un tournoi fort avec quatre sommets ne peut pas être arête-pancyclique.

Le théorème de Turán stipule que tout graphe non orienté à ${\displaystyle n}$ sommets avec au moins ${\displaystyle n^{2}/4}$ arêtes, et sans arêtes multiples ou boucles, contient soit un triangle, soit le graphe biparti complet ${\displaystyle K_{n/2,n/2}}$. Ce théorème peut être précisé : tout graphe hamiltonien non orienté avec au moins ${\displaystyle n^{2}/4}$ arêtes arêtes est soit pancyclique soit égal à ${\displaystyle K_{n/2,n/2}}$[1].

Il existe des graphes orientés hamiltoniens à ${\displaystyle n}$ sommets avec ${\displaystyle n(n+1)/2-3}$ arcs qui ne sont pas pancycliques, mais un graphe orienté hamiltonien avec au moins ${\displaystyle n(n+1)/2-1}$ arcs est pancyclique. De plus, tout graphe orienté à ${\displaystyle n}$ sommets fortement connexe dans lequel chaque sommet est de degré au moins ${\displaystyle n}$ (en comptant les arêtes entrantes et les sortantes) est soit pancyclique, soit un graphe orienté bipartite complet[13].

Pour tout graphe ${\displaystyle G}$, la ${\displaystyle k}$-ième puissance ${\displaystyle G^{k}}$ est définie comme le graphe sur le même ensemble de sommets qui a une arête entre deux sommets dont la distance dans ${\displaystyle G}$ est au plus ${\displaystyle k}$. Si ${\displaystyle G}$ est sommet-connexe, alors d'après le théorème de Fleischner son carré ${\displaystyle G^{2}}$ est hamiltonien ; on peut montrer qu'il est nécessairement sommet-pancyclique[14]. Plus généralemment, si ${\displaystyle G^{2}}$ est hamiltonien, il est également pancyclique[15].

Il est NP-complet de tester si un graphe est pancyclique, même dans le cas particulier des graphes cubiques 3-connexes, et il est aussi NP-complet de tester si un graphe est sommet-pancyclique, même dans le cas particulier des graphes polyédriques[16]. Il est également NP-complet de tester si le carré d'un graphe est hamiltonien, et donc s'il est pancyclique[17].

Les graphes pancycliques ont été étudiés pour la première fois dans le contexte des tournois par Harary et Moser (1966), Moon (1966) et Alspach (1967)). Le concept de pancyclicité a été nommé et étendu aux graphes non orientés par Bondy. Un travail plus récent est la thèse de Zengxian Tian[18].

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Pancyclic graph » (voir la liste des auteurs).

• (en) Eric W. Weisstein, « Pancyclic Graph », sur MathWorld

• Portail des mathématiques
• Portail de l'informatique théorique