Théorie des lignes portantes

La théorie des lignes portantes de Prandtl[1] est un modèle qui prédit la distribution de la portance sur une aile tri-dimensionnelle basée sur sa géométrie. Elle est aussi appelée théorie des ailes de Lanchester–Prandtl[2].

La théorie fut formulée indépendamment[3] par Frederick Lanchester en 1907[4], et par Ludwig Prandtl en 1918–1919[5] après avoir travaillé avec Albert Betz et Max Munk.

Dans ce modèle, le vortex perd de l'efficacité latéralement le long de l'aile car il est dévié par une nappe de vortex provenant de l'arrière de l'aile plutôt que de juste à partir des extrémités des ailes[6]^,[7].

La théorie s'applique particulièrement bien aux planeurs modernes et aux avions de transport de ligne qui ont de longues ailes effilées.

Introduction

Une distribution non réaliste de la distribution de la portance en négligeant les effets 3D.

Distribution de la portance observée sur une aile trapézoïdale.

Pour une aile tri-dimensionnelle finie, la portance linéique diffère d'un point de l'aile à un autre le long de l'aile. Elle ne correspond pas simplement à la portance estimée par le modèle bi-dimensionnel. En fait, la portance d'une section est fortement influencée par les portances des sections au voisinage.

Il est donc difficile (mais pas impossible) d'exprimer analytiquement le champ de portance qu'une aile de géométrie donnée va créer. La théorie des ailes portantes donne la distribution du vecteur portance (linéique) suivant la direction y de l'envergure de l'aile. La distribution L' de la portance linéique dépend de la forme de l'aile (longueur de la corde c(y) en une section y donnée, cambrure et torsion de l'aile), de la masse volumique de l'air ρ, de la vitesse de l'air à l'infini ( $V_{\infty }{\vec {i}}$ ) et de l'angle d'attaque à l'infini $\alpha _{\infty }$ .

Principe

La théorie des lignes portantes utilise la conception de circulation et le théorème de Kutta-Jukowski qui affirme que :

{\tilde {L}}(y)=\rho V\Gamma (y)

Ainsi, la détermination de la fonction de distribution de la portance linéique se ramène à la distribution de la circulation dans le sens de l'envergure, $\Gamma _{(y)}$ .

La modélisation (inconnue et à déterminer) de la portance linéique locale (aussi à déterminer) nous permet de tenir compte de l'influence d'une section sur les sections voisines. Dans cette perspective, tout changement de la portance linéique le long de l'envergure est équivalent à un changement de la circulation le long de l'envergure. D'après les théorèmes de Helmholtz, un vortex en forme de filament ne peut pas finir au milieu de nulle part et est donc soit une boucle fermée soit se prolonge jusqu'à l'infini. Ainsi, tout changement de la portance linéique peut être modélisé par un filament correspondant au vortex en forme de fer à cheval emporté par le flot à l'arrière de l'aile.

Ce vortex dévié dont la force est égale à la dérivée de la distribution de circulation (inconnue), ${\operatorname {d} \Gamma \over \operatorname {d} y}$ , influence le flot à gauche et à droite de la section d'aile.

Cette influence latérale (flot ascendant au-delà de l'extrémité de l'aile et l'écoulement descendant en deçà) est la pierre angulaire de la théorie des lignes de portance. Ainsi, si la variation de la distribution de la portance linéique est connue pour une section donnée, il est possible de prédire comment cette section influence la portance sur ses voisines : la vitesse verticale induite w peut être quantifiée en utilisant la distribution de la vitesse à l'intérieur d'un vortex et en relation avec la variation de l'angle d'attaque effectif des sections voisines.

Formellement, la variation locale de l'angle d'attaque induit $\alpha _{i}$ pour une section donnée peut être quantifiée comme étant la somme infinie (intégrale) des vitesses induites par les autres sections de l'aile. En retour, l'intégrale des vitesses induites sur chaque section de l'aile correspond à la portance totale désirée.

Ceci conduit à la résolution d'une équation intégro-différentielle du type $L_{total}=\rho V_{\infty }\int _{\rm {bout}}^{\rm {bout}}\Gamma (y)\operatorname {d} y$ où $\Gamma (y)$ est exprimée seulement en fonction de la forme de l'aile, de la variation dans le sens de l'envergure de la circulation ${\operatorname {d} \Gamma (y) \over \operatorname {d} y}$ . La solution de ladite équation est une fonction $\Gamma (y)$ , qui représente de manière précise la distribution de la circulation le long d'une aile en fonction de sa forme (géométrie).

Expression de la portance et de la circulation

Nomenclature

$b$ est l'envergure de l'aile.
$S$ est la surface alaire
$\ C_{L}$ est le coefficient de portance global
$\lambda =b^{2}/S$ est l'allongement
$\ \alpha _{\infty }$ est l'angle d'attaque eu égard le flot à l'infini
$\ V_{\infty }$ est la vitesse air de l'aéronef (m/s)
$\ C_{D_{i}}$ est le coefficient de traînée induite
$\ e$ est le coefficient d'Oswald[Note 1]

Les variables suivantes dépendent de la position dans le sens de l'envergure y

$\ C_{l}$ le coefficient de portance en 2 dimensions
$\ \Gamma$ est la circulation circulation sur une section d'aile (m²/s)
$\ c$ est la longueur de la corde à une position donnée
$\ \alpha _{geo}$ est le changement local de l'angle d'attaque eu égard le vrillage de l'aile
$\ \alpha _{0}$ est l'angle d'attaque engendrant une portance nulle
$\ C_{l_{\alpha }}=2\pi$ est le coefficient de proportionnalité définissant le coefficient de portance en fonction de l'angle d'attaque effectif.
$\ w$ est le downwash (déflexion vers le bas)

Formulaire

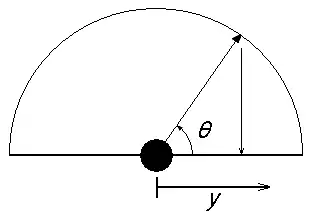
On définit l'angle $\theta$ tel que :

y=-{\frac {b}{2}}\cos(\theta )

La circulation en y s'exprime comme suit :

\ \Gamma (\theta )=2bV_{\infty }\sum _{n\in \mathbb {N} }A_{n}\sin(n\theta )

où les A_n sont solution de l'équation linéaire infinie suivante :

2b\sum _{n\geq 1}A_{n}\sin(n\theta )=\pi \left(\alpha -\alpha _{0}-\sum _{n\geq 1}nA_{n}{\sin(n\theta ) \over \sin \theta }\right)c(y)

La portance s'exprime par :

L={1 \over 2}C_{L}\rho SV_{\infty }^{2}

La traînée induite s'exprime par :

D_{i}={1 \over 2}C_{D_{i}}\rho SV_{\infty }^{2}

Le coefficient de portance s'exprime comme suit :

C_{L}=\pi A_{\lambda }

où l'allongement vaut $\lambda ={b^{2} \over S}$ et S est l'aire de l'aile.

Le coefficient d'Oswald e est:

e=\left[1+\sum _{n\geq 2}n\left({A_{n} \over A_{1}}\right)^{2}\right]^{2}

Le coefficient de traînée induite vaut[6]^,[7]^,[8]^,[9] :

C_{D_{i}}={C_{L}^{2} \over \pi \lambda e}

Si l'aile est symétrique, l'on a :

A_{2}=A_{4}=A_{6}=\ldots =0

Dans le cas d'une aile elliptique, on a e = 1. La circulation est :

\Gamma (\theta )={2bCV_{\infty } \over 2b-C}\pi (\alpha -\alpha _{0})\sin \theta

où C est la corde au milieu de l'aile.

Calculs détaillés

La preuve du formulaire supra est longue et pénible et est donnée dans la boîte déroulante infra.

Calculs détaillés

Calcul des coefficients de portance et de trainée

Soit le changement de variable suivant :

\ y_{0}=-{\frac {b}{2}}\cos(\theta )

et supposons que la solution de $\ \Gamma _{aile}$ est une série de Fourier suivante :

\ \Gamma (\theta )=2bV_{\infty }\sum _{n\in \mathbb {N} }A_{n}\sin(n\theta )

On peut arbitrairement choisir A₀ = 0.

On cherche à déterminer ces coefficients A_n[Note 2].

La section infinitésimale de largeur $\ dy$ le long de l'envergure de l'aile apporte une portance linéique ${\tilde {L}}$ , il faut intégrer toutes les portances linéiques pour avoir la portance du profil. Pour le bout de profil infinitésimal de largeur $\ dy$ , le Théorème de Kutta-Jukowski donne :

\ {\tilde {L}}=\rho V_{\infty }\Gamma =\rho V_{\infty }{\frac {1}{2}}{\frac {dC_{L_{2D}}}{d\alpha }}c(y)V_{\infty }(\alpha _{\text{effectif}}-\alpha _{0}(y)+\Phi (y))

d'où

\ L=\int _{-{\frac {b}{2}}}^{+{\frac {b}{2}}}{\tilde {L}}\ dy={\frac {1}{2}}\rho {V_{\infty }}^{2}\int _{-{\frac {b}{2}}}^{+{\frac {b}{2}}}a_{0}(y)c(y)[\alpha _{\text{effectif}}-\alpha _{0}(y)+\Phi (y)]dy=\rho V_{\infty }\int _{-{\frac {b}{2}}}^{+{\frac {b}{2}}}\Gamma dy

Idem pour la trainée induite ${\tilde {D}}$ sachant que :

{\tilde {D}}\approx {\tilde {L}}\epsilon \approx l\epsilon

et

\ D=\int _{-{\frac {b}{2}}}^{+{\frac {b}{2}}}{\tilde {D}}.dy

La littérature pour la portance et la traînée préfère utiliser des équations avec des coefficients adimensionnels. Les formules sont :

\ L={\frac {1}{2}}S\rho {V_{\infty }}^{2}C_{L}

et

\ D={\frac {1}{2}}S\rho {V_{\infty }}^{2}C_{D_{i}}

avec

\ C_{L}={\frac {2}{SV_{\infty }}}\int _{-{\frac {b}{2}}}^{+{\frac {b}{2}}}\Gamma dy

et

\ C_{d_{i}}={\frac {2}{SV_{\infty }}}\int _{-{\frac {b}{2}}}^{+{\frac {b}{2}}}\Gamma (y)\epsilon (y)dy

On rappelle que $\epsilon =w/V_{\infty }$ . On ligne de sillage arrière est semi infinie et donc on applique la loi de Biot-Savart pour une tige (vortex) semi-infinie. En outre, le downwash engendré par un vortex de sillage $\delta \Gamma (y)$ en y₀ est[10]:

dw(y_{0})={\delta \Gamma (y) \over 4\pi (y-y_{0})}

et donc,

w(y_{0})=\int _{-b/2}^{b/2}{d\Gamma (y) \over 4\pi (y-y_{0})}

On dérive la fonction Γ et donc:

{d\Gamma (y) \over dy}={d\Gamma  \over d\theta }{d\theta  \over dy}

On a : ${dy \over d\theta }={b \over 2}\sin \theta$

Donc,

{d\Gamma (\theta ) \over d\theta }=2bV_{\infty }\sum _{n\geq 1}nA_{n}\cos(n\theta )

Et donc,

{d\Gamma (y) \over dy}=2bV_{\infty }\sum _{n\geq 1}{2 \over b}nA_{n}{\cos(n\theta ) \over \sin \theta }

Finalement,

{d\Gamma (y) \over dy}=4V_{\infty }\sum _{n\geq 1}nA_{n}{\cos(n\theta ) \over \sin \theta }

Le downwash en y₀ avec $y_{0}={b \over 2}\cos \phi$ est donc :

w(\phi )=\int _{-b/2}^{b/2}{d\Gamma (y) \over dy}\ {1 \over 4\pi (y-y_{0})}dy=4V_{\infty }\sum _{n\geq 1}\int _{0}^{\pi }\left(nA_{n}{\cos(n\theta ) \over \sin \theta \ (-b/2)(4\pi )(\cos \theta -\cos \phi )}\right){-b \over 2}\sin \theta d\theta

Donc,

w(\phi )={V_{\infty } \over \pi }\sum _{n\geq 1}\int _{0}^{\pi }\left(nA_{n}{\cos(n\theta ) \over (\cos \theta -\cos \phi )}\right)d\theta

On utilise l'intégrale de Glauert

\int _{0}^{\pi }{\cos(n\theta ) \over \cos(\theta )-\cos(\phi )}d\theta =\pi {\sin(n\phi ) \over \sin \phi }

Et donc,

w(\phi )={V_{\infty } \over \pi }\sum _{n\geq 1}\left(nA_{n}\pi {\sin(n\phi ) \over \sin \phi }\right)

On remplace $\phi$ par $\theta$ et on rappelle que

\epsilon (\theta )={w(\theta ) \over V_{\infty }}

.

Donc,

\epsilon (\theta )=\sum _{n\geq 1}nA_{n}{\sin(n\theta ) \over \sin \theta }

On rappelle que

C_{D_{i}}={2 \over SV_{\infty }}\int _{-{b \over 2}}^{b \over 2}\Gamma (y)\epsilon (y)dy

Donc,

C_{D_{i}}={2 \over SV_{\infty }}\int _{0}^{\pi }\Gamma (\theta )\epsilon (\theta ){b \over 2}\sin \theta d\theta

Donc,

C_{D_{i}}=-{2 \over SV_{\infty }}\sum _{n\geq 1}\sum _{m\geq 1}\int _{0}^{\pi }(2bV_{\infty })A_{n}\sin(n\theta )\times \pi mA_{m}{\sin(m\theta ) \over \sin \theta }\sin \theta (b/2)d\theta

Donc,

C_{D_{i}}=-{2 \over SbV_{\infty }}{2b^{2}V_{\infty } \over 2}\sum _{n\geq 1}\sum _{m\geq 1}\int _{0}^{\pi }A_{n}\sin(n\theta )\times \pi mA_{m}{\sin(m\theta ) \over \sin \theta }\sin \theta d\theta

Donc,

C_{D_{i}}=-{2b^{2} \over Sb}\sum _{n\geq 1}\sum _{m\geq 1}\int _{0}^{\pi }A_{n}A_{m}m[\cos((n+m)\theta )-\cos((n-m)\theta )]d\theta

Si $n\neq m$ , l'intégrale est nulle. Donc,

C_{D_{i}}=-{2b^{2} \over S}\sum _{n\geq 1}\int _{0}^{\pi }nA_{n}^{2}[\cos(2n\theta )-\cos(0\theta )]d\theta

Le premier terme est nul et donc,

C_{D_{i}}=-{2b^{2} \over S}\sum _{n\geq 1}\times {-\pi  \over 2}nA_{n}^{2}

Donc,

C_{D_{i}}={\pi b^{2} \over S}\sum _{n\geq 1}nA_{n}^{2}

On rappelle que :

\ C_{L}={\frac {2}{SV_{\infty }}}\int _{-{\frac {b}{2}}}^{+{\frac {b}{2}}}\Gamma dy=\int _{0}^{\pi }{b \over 2}\Gamma (\theta )\sin \theta d\theta

On substitue.

\ C_{L}={2 \over SV_{\infty }}\int _{0}^{\pi }{b \over 2}(2bV_{\infty }){b \over 2}\left(\sum _{n\geq 1}A_{n}\sin(n\theta )\right)\sin \theta d\theta

On écrit donc :

\ C_{L}={\frac {2}{SV_{\infty }}}\times {b^{2} \over 2V_{\infty }}\int _{0}^{\pi }\left(\int _{0}^{\pi }\sin \theta \sin \theta d\theta +\sum _{n\geq 2}A_{n}\int _{0}^{\pi }\sin(n\theta )\right)\sin \theta d\theta

Donc,

\ C_{L}={2S \over b^{2}}\int _{0}^{\pi }\left(\int _{0}^{\pi }\sin \theta \sin \theta d\theta +\sum _{n\geq 2}A_{n}\int _{0}^{\pi }\sin(n\theta )\right)\sin \theta d\theta

On considère $n\geq 2$ . On a :

\int _{0}^{\pi }\sin(n\theta )\sin \theta d\theta =\int _{0}^{\pi }{1 \over 2}(\cos(n-1)\theta -\cos(n+1)\theta )d\theta

On effectue un changement de variable $p\theta =\xi$ pour $p\geq 1$ et donc :

\int _{0}^{\pi }\cos p\theta d\theta ={1 \over p}\int _{0}^{p\pi }\cos \xi d\xi =\sin(p\pi )-\sin 0=0-0=0

Et donc,

\ C_{L}={2S \over b^{2}}\int _{0}^{\pi }{b \over 2}\left(\int _{0}^{\pi }\sin \theta \sin \theta d\theta +\sum _{n\geq 2}A_{n}0\right)

On note que :

\int _{0}^{\pi }\sin ^{2}\theta d\theta ={\pi  \over 2}

Donc,

C_{L}={2b^{2} \over S}{\pi  \over 2}A_{1}={\pi A_{1}b^{2} \over S}

Finalement :

A_{1}={S \over \pi b^{2}}C_{L}

On substitue :

C_{D_{i}}={\pi b^{2} \over S}\left(A_{1}^{2}+\sum _{n\geq 1}nA_{n}^{2}\right)

Donc,

C_{D_{i}}={\pi b^{2} \over S}A_{1}^{2}\left[1+\sum _{n\geq 2}n\left({A_{n} \over A_{1}}\right)^{2}\right]

On définit le coefficient d'Oswald

{1 \over e}=1+\sum _{n\geq 2}n\left({A_{n} \over A_{1}}\right)^{2}

Donc,

C_{D_{i}}={\pi b^{2} \over S}A_{1}^{2}\times {1 \over e}

On remplace A₁ et donc :

C_{D_{i}}={\pi b^{2} \over Se}\left({S \over \pi b^{2}}\right)^{2}C_{L}^{2}

Donc,

C_{D_{i}}=C_{L}^{2}{S \over b^{2}\pi e}

On a $S=b\times c$ où c est la longueur de la corde moyenne. Donc,

C_{D_{i}}=C_{L}^{2}{b\times c \over b^{2}\pi e}=C_{L}^{2}{c \over b}\times {1 \over \pi e}

On définit l'allongement $\lambda ={b^{2} \over S}$ . Et finalement on obtient la formule souvent postulée :

C_{D_{i}}={C_{L}^{2} \over \pi \lambda e}

Dans le cas d'une aile rectangulaire, on a $S=b\times c$ et l'allongement devient :

\lambda ={b^{2} \over S}={b^{2} \over bc}={b \over c}

Quelle que soit la forme de l'aile, le coefficient de traînée inductive est proportionnel à $C_{L}^{2}$ .

Dans le cas d'une aile symétrique, on a :

\Gamma (y)=\Gamma (-y)

et donc : $\Gamma (\theta )=\Gamma (\pi -\theta )$

On a vu que :

\ \Gamma (\theta )=2bV_{\infty }\sum _{n\in \mathbb {N} }A_{n}\sin(n\theta )

\Gamma (\pi -\theta )=2bV_{\infty }\sum _{n\in \mathbb {N} }A_{n}\sin(n\pi -n\theta )

On a :

\sin(n\pi -n\theta )=\sin(n\pi )\cos(n\theta )-\cos(n\pi )\sin(n\theta )

On rappelle que $\sin(n\pi )=0$ et que $\cos(n\pi )=(-1)^{n}$ et donc :

\sin(n\pi -n\theta )=-(-1)^{n}\sin(n\theta )

On obtient alors l'égalité $\forall \theta \in [0,\pi ]$ :

2bV_{\infty }\sum _{n\in \mathbb {N} }A_{n}\sin(n\theta )=\Gamma (\theta )=\Gamma (\pi -\theta )=2bV_{\infty }\sum _{n\in \mathbb {N} }(-1)^{n+1}A_{n}\sin(n\theta )

Donc,

\sum _{n\in \mathbb {N} }A_{n}(\sin(n\theta )(1-(-1)^{n+1})=0

Donc,

\sum _{n\in \mathbb {N} }A_{n}(\sin(n\theta )(1+(-1)^{n})=0

Si n est pair, on doit avoir $''A''<sub>n</sub>=0$

Donx, $A_{2}=A_{4}=A_{6}=\ldots =0$

Résolution de l'équation de Prandtl

Soit $\alpha =-\alpha _{0}+\alpha$ l'angle d'attaque en ignorant le downwash. Soit $\epsilon$ l'angle du downwash. L'angle d'attaque effectif sera donc :

\alpha _{\rm {eff}}=\alpha -\alpha _{0}-\epsilon

Le coefficient de portance en un point y est : $C_{l}(y)=2\pi \alpha _{\rm {eff}}(y)$

La portance linéique ${\tilde {L}}(y)$ est :

{\tilde {L}}=\rho V_{\infty }\Gamma (y)

Et aussi :

{\tilde {L}}={1 \over 2}\rho C_{l}(y)V_{\infty }^{2}={1 \over 2}\rho 2\pi \alpha _{\rm {eff}}c(y)V_{\infty }^{2}

Donc,

{\tilde {L}}=\rho \pi (\alpha -\alpha _{0}-\epsilon )c(y)V_{\infty }^{2}

Donc,

\rho V_{\infty }\Gamma (y)={\tilde {L}}=\rho \pi (\alpha -\alpha _{0}-\epsilon )c(y)V_{\infty }^{2}

D'où une simplification :

\Gamma (y)=\pi (\alpha -\alpha _{0}-\epsilon )c(y)V_{\infty }

On remplace Γ et ε et donc :

2bV_{\infty }\sum _{n\geq 1}A_{n}\sin(n\theta )=\pi \left(\alpha -\alpha _{0}-\sum _{n\geq 1}nA_{n}{\sin(n\theta ) \over \sin \theta }\right)c(y)V_{\infty }

Et donc :

2b\sum _{n\geq 1}A_{n}\sin(n\theta )=\pi \left(\alpha -\alpha _{0}-\sum _{n\geq 1}nA_{n}{\sin(n\theta ) \over \sin \theta }\right)c(y)

On obtient donc un système linéaire «infini» que l'on doit résoudre.

Cas d'une aile elliptique

On considère maintenant une aile elliptique où :

\left({c(y) \over C/2}\right)^{2}+\left({y \over b/2}\right)^{2}=1

Comme l'on a:

{y \over b/2}=-\cos \theta

On en déduit que

\left({c(y) \over C/2}\right)^{2}+\cos ^{2}\theta =1

Donc,

\left({c(y)/2 \over C/2}\right)^{2}=1-\cos ^{2}\theta =\sin ^{2}\theta

On rappelle que $c(y)>0$ . Donc,

{c(y) \over C}=\sin \theta

Donc,

c(y)=C\sin \theta

On revient ausystème linéaire infini. On a:

2b\sum _{n\geq 1}A_{n}\sin(n\theta )=\pi \left(\alpha -\alpha _{0}-\sum _{n\geq 1}nA_{n}{\sin(n\theta ) \over \sin \theta }\right)C\sin \theta

Et donc :

2b\sum _{n\geq 1}A_{n}\sin(n\theta )=\pi \left((\alpha -\alpha _{0})\sin \theta -\sum _{n\geq 1}nA_{n}\sin(n\theta )\right)C

Et donc :

\sum _{n\geq 1}A_{n}\sin(n\theta )\left(2b-{C \over 2}\right)=\pi (\alpha -\alpha _{0})C\sin \theta

On constate immédiatement que pour $n\geq 2$ , on a : A_n = 0

Et donc :

A_{1}\left(2b-C\right)=\pi (\alpha -\alpha _{0})C

En outre, le coefficient d'Oswald vaut l'unité et donc l'on a :

C_{D_{i}}={C_{L}^{2} \over \pi \lambda }

L'aire de l'ellipse est $S=\pi {bC \over 4}$ .

Donc l'allongement est :

\lambda ={b^{2} \over S}={4b^{2} \over \pi bC}={4 \over \pi }{b \over C}

On obtient donc :

C_{D_{i}}={C_{L}^{2} \over \pi {4 \over \pi }\times {b \over C}}=C_{L}^{2}{C \over 4b}

En outre,

A_{1}=\pi (\alpha -\alpha _{0}){C \over 2b-C}

Et donc la distribution de circulation est :

\Gamma (\theta )={2bV_{\infty }}\pi (\alpha -\alpha _{0}){C \over 2b-C}\sin \theta

Et donc :

\Gamma (\theta )={2bCV_{\infty } \over 2b-C}\pi (\alpha -\alpha _{0})\sin \theta

On obtient donc une distribution purement sinusoïdale de la circulation et donc de la poussée linéique.

Déflexion des ailerons

L'effet des ailerons peut être pris en compte en ajustant la valeur de α₀. Si les ailerons sont asymétriques, la valeur de α₀ est différente pour chaque côté.

Approximations en pratique

On peut en pratique écrire que :

\ C_{L}=2\pi {\lambda  \over \lambda +2}\alpha

où

$\ C_{\text{L}}$ est le coefficient de portance;
$\lambda$ est l'allongement; et
$\ \alpha$ est l'angle d'attaque.

On remarque que cette équation devient l'équation donnée dans la théorie des profils minces lorsque l'allongement $\lambda \to \infty$ [11].

Annexe : Calcul de l'intégrale de Glauert

Démonstration de la formule donnant l'intégrale de Glauert

On considère la fonction

f(\theta )={\cos(n\theta ) \over \cos \theta -\cos \theta _{0}}

On veut calculer l'intégrale $\int _{-\pi }^{\pi }f(\theta )d\theta$ . Strictement parlant, une telle intégrale n'a pas de sens. Toutefois, on va utiliser le théorème des résidus. On pose $z_{0}=e^{i\theta _{0}}$ On définit :

F_{r}(z)={1 \over z}\times {z^{n} \over z+1/z-z_{0}-1/z_{0}-2ir}

On a donc:

F(z)={z^{n} \over z^{2}+1-zz_{0}-z/z_{0}-2irz}={z^{n} \over z^{2}+z(2\cos \theta _{0}+2ir)+1}

Lorsque r = 0 , on a:

F(z)={z^{n} \over (z-z_{0})(z-1/z_{0})}

On considère le contour C constitué du cercle de rayon unité. On a:

\int _{C}F_{r}(z)dz=2i\pi {\rm {Res}}F_{r}(z_{0}+e(r))

où e(r) tend vers 0 lorsque r tend vers 0. Le résidu de cette fonction en z₀ + e(r) est

{\rm {Res}}F(z_{0}+e(r))={(z_{0}+e(r))^{n} \over z_{0}+e(r)-1/(z_{0}+e(r))}

On a:

z_{0}^{n}=\cos(n\theta )+i\sin(n\theta )\qquad {1 \over z_{0}-1/z_{0}}={1 \over 2i\sin \theta _{0}}

On effectue un développement limité et l'on obtient donc :

{\rm {Res}}F(z_{0}+e(r))={\cos(n\theta )+i\sin(n\theta )+e_{1}(r) \over 2i\sin \theta _{0}+e_{2}(r)}

Donc,

\int _{C}F_{r}(z)dz=2\pi i\times {\cos(n\theta _{0})+i\sin(n\theta _{0})+e_{1}(r) \over 2i\sin \theta _{0}+e_{2}(r)}=\pi \times {\cos(n\theta _{0})+i\sin(n\theta _{0})+e_{1}(r) \over \sin \theta _{0}+ie_{2}(r)}

On a :

\int _{C}F_{r}(z)dz=\int _{0}^{2\pi }{[e^{i\theta }]^{n-1} \over e^{i\theta }+[e^{i\theta }]^{-1}-e^{i\theta _{0}}-[e^{i\theta _{0}}]^{-1}+2ir}d[e^{i\theta }]

Donc :

\int _{C}F_{r}(z)dz=\int _{0}^{2\pi }{[e^{i\theta }]^{n-1}ie^{i\theta }d\theta  \over \cos \theta +i\sin \theta +\cos \theta -i\sin \theta -2\cos \theta _{0}+2ir}

Donc :

\int _{C}F_{r}(z)dz=\int _{0}^{2\pi }i{\cos(n\theta )+i\sin(n\theta ) \over 2\cos \theta -2\cos \theta _{0}+2ir}d\theta

On « simplifie » le dénominateur et donc :

\int _{C}F_{r}(z)dz=\int _{0}^{2\pi }{(i\cos(n\theta )-\sin(n\theta ))\times (\cos \theta -\cos \theta _{0}-ir) \over (2\cos \theta -2\cos \theta _{0}+2ir)(\cos \theta -\cos \theta _{0}-ir)}d\theta

En combinant, on obtient donc :

\pi \times {\cos(n\theta _{0})+i\sin(n\theta _{0})+e_{1}(r) \over \sin \theta _{0}+ie_{2}(r)}=\int _{C}F_{r}(z)dz=\int _{0}^{2\pi }{i\cos(n\theta )-\sin(n\theta ) \over 2\cos \theta -2\cos \theta _{0}+2ir}d\theta

On considère la partie imaginaire de cette identité et donc :

{\rm {Im}}\left(\pi \times {\cos(n\theta _{0})+i\sin(n\theta _{0})+e_{1}(r) \over \sin \theta _{0}+ie_{2}(r)}\right)={\rm {Im}}\left(\int _{0}^{2\pi }{(i\cos(n\theta )-\sin(n\theta ))\times (\cos \theta -\cos \theta _{0}-ir) \over 2(\cos \theta -\cos \theta _{0})^{2}+2r^{2}}d\theta \right)

Donc,

\pi \times {\sin(n\theta _{0}) \over \sin \theta _{0}}+e_{3}(r)=\int _{0}^{2\pi }{(\cos(n\theta )(\cos \theta -\cos \theta _{0})+r\sin(n\theta ) \over 2(\cos \theta -\cos \theta _{0})^{2}+2r^{2}}d\theta

La limite du deuxième terme tend vers 0. On a donc:

\lim _{r\to 0}\left(\pi \times {\sin(n\theta _{0}) \over \sin \theta _{0}}+e_{3}(r)\right)=\lim _{r\to 0}\left(\int _{0}^{2\pi }{(\cos(n\theta )(\cos \theta -\cos \theta _{0})+r\sin(n\theta ) \over 2(\cos \theta -\cos \theta _{0})^{2}+2r^{2}}d\theta \right)=\lim _{r\to 0}\left(\int _{0}^{2\pi }{(\cos(n\theta )(\cos \theta -\cos \theta _{0}) \over 2(\cos \theta -\cos \theta _{0})^{2}+2r^{2}}d\theta \right)

Donc,

{\pi \sin(n\theta _{0}) \over \sin \theta _{0}}=\int _{0}^{2\pi }{\cos(n\theta )(\cos \theta -\cos \theta _{0}) \over 2(\cos \theta -\cos \theta _{0})^{2}}d\theta

On « simplifie » (cette opération est discutable) :

{\pi \sin(n\theta _{0}) \over \sin \theta _{0}}=\int _{0}^{2\pi }{\cos(n\theta ) \over 2\cos \theta -2\cos \theta _{0}}d\theta

La fonction cosinus est paire et donc:

\pi \times {\sin(n\theta _{0}) \over \sin \theta _{0}}=\int _{0}^{2\pi }{\cos(n\theta ) \over 2\cos \theta -2\cos \theta _{0}}d\theta =2\int _{0}^{\pi }{\cos(n\theta ) \over 2\cos \theta -2\cos \theta _{0}}d\theta =\int _{0}^{\pi }{\cos(n\theta ) \over \cos \theta -\cos \theta _{0}}d\theta

ce qui démontre le résultat.

Limites de la théorie

La théorie des profils minces n'entre pas en ligne de compte :

Fluide compressible
Viscosité
Ailes d'allongement réduit
Écoulement instable

Voir aussi

Notes et références

Notes

Le coefficient d'Oswald est ignoré dans l'ouvrage de l'US Navy [8].
Attention, il ne faut pas confondre ces $\ A_{n}$ ici en trois dimensions avec ceux en deux dimensions. Bien que la littérature utilise la même notation, ils sont différents.

Références

(en) Anderson, John D., Fundamental of aerodynamics, McGraw-Hill, Boston, 2001, 1106 p. (ISBN 0-07-237335-0), p. 360
(en) Houghton, E. L. et Carpenter, P.W., Aerodynamics for Engineering Students, Butterworth Heinmann, 2003, 5^e éd., 590 p. (ISBN 0-7506-5111-3)
(en) Theodore von Kármán, Aerodynamics : Selected Topics in the Light of their Historical Development, Cornell University Press (reproduced by Dover in 2004), 1954, 203 p. (ISBN 0-486-43485-0, lire en ligne)
Lanchester, Frederick W., Aerodynamics, 1907 (lire en ligne)
(de) Ludwig Prandtl, Tragflügeltheorie, 1921
(en) Ira H. Abbott, et Von Doenhoff, Albert E., Theory of Wing Sections Section 1.4, Dover, 693 p.
(en) Clancy, L.J., Aerodynamics Section 8.11, John Wiley & Sons, 1975, 1^re éd., 610 p. (ISBN 978-0-470-15837-1)
(en) Hugh Harrison Hurt, Aerodynamics for naval aviators, US Navy, 1959, 416 p. (ISBN 978-1-939878-18-2, lire en ligne), p. 68
(en) Frank Irving, The Paths of Soaring Flight, Imperial College Press, 1999, 131 p. (ISBN 978-1-86094-055-2), p. 12
(en)« Prandtl Lifting Line Theory (for 3-D wings) » (consulté le 23 juillet 2013)
(en) « Lift Coefficient & Thin Airfoil Theory » (consulté le 28 novembre 2017)

Portail de la physique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[9] Le coefficient d'Oswald est ignoré dans l'ouvrage de l'US Navy [8].

[11] Attention, il ne faut pas confondre ces $\ A_{n}$ ici en trois dimensions avec ceux en deux dimensions. Bien que la littérature utilise la même notation, ils sont différents.

[1] (en) Anderson, John D., Fundamental of aerodynamics, McGraw-Hill, Boston, 2001, 1106 p. (ISBN 0-07-237335-0), p. 360

[2] (en) Houghton, E. L. et Carpenter, P.W., Aerodynamics for Engineering Students, Butterworth Heinmann, 2003, 5^e éd., 590 p. (ISBN 0-7506-5111-3)

[3] (en) Theodore von Kármán, Aerodynamics : Selected Topics in the Light of their Historical Development, Cornell University Press (reproduced by Dover in 2004), 1954, 203 p. (ISBN 0-486-43485-0, lire en ligne)

[4] Lanchester, Frederick W., Aerodynamics, 1907 (lire en ligne)

[5] (de) Ludwig Prandtl, Tragflügeltheorie, 1921

[Abbott-6] (en) Ira H. Abbott, et Von Doenhoff, Albert E., Theory of Wing Sections Section 1.4, Dover, 693 p.

[Clancy-7] (en) Clancy, L.J., Aerodynamics Section 8.11, John Wiley & Sons, 1975, 1^re éd., 610 p. (ISBN 978-0-470-15837-1)

[Navy-8] (en) Hugh Harrison Hurt, Aerodynamics for naval aviators, US Navy, 1959, 416 p. (ISBN 978-1-939878-18-2, lire en ligne), p. 68

[10] (en) Frank Irving, The Paths of Soaring Flight, Imperial College Press, 1999, 131 p. (ISBN 978-1-86094-055-2), p. 12

[liftline-12] (en)« Prandtl Lifting Line Theory (for 3-D wings) » (consulté le 23 juillet 2013)

[13] (en) « Lift Coefficient & Thin Airfoil Theory » (consulté le 28 novembre 2017)