Triakitétraèdre tronqué

Le triakitétraèdre tronqué est un polyèdre convexe à 16 faces : 4 groupes de 3 pentagones rattachés aux mêmes sommets, et 4 hexagones dans les trous. Il est obtenu par la troncature des 4 sommets d'un triakitétraèdre où il y avait 6 faces réunies. Les quatre hexagones qui le composent sont réguliers, mais les 12 pentagones sont irréguliers.

Triakitétraèdre tronqué

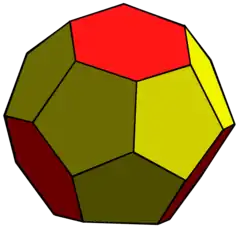Type	Quasi-solide de Johnson
Faces	4 hexagones 12 pentagones
Arêtes	42
Sommets	28
Configurations de sommets	4 (5.5.5) 24 (5.5.6)
Groupe de symétrie	T_d
Propriétés	convexe

Un polyèdre topologiquement équivalent peut être construit en utilisant 12 pentagones réguliers et 4 hexagones réguliers (mais les faces hexagonales seront très légèrement ondulées en raison de l'inexactitude des angles).

Le triakitétraèdre tronqué est un quasi-solide de Johnson : il est convexe, mais ses faces ne sont pas strictement régulières. C'est aussi le cas du dodécaèdre rhombique tronqué et du triacontaèdre rhombique tronqué.

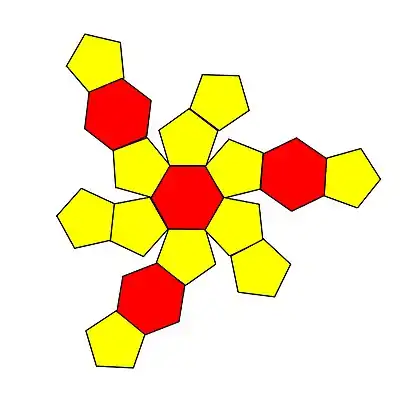
Patron

Voici le patron d'un triakitétraèdre tronqué :

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Truncated triakis tetrahedron » (voir la liste des auteurs).

Voir aussi

Articles connexes

Triakitétraèdre
Autres quasi-solides de Johnson :
- Dodécaèdre rhombique tronqué
- Triacontaèdre rhombique tronqué

Liens externes

Quasi-solide de Johnson n^o 16

Portail de la géométrie

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.