Dodécaèdre rhombique tronqué
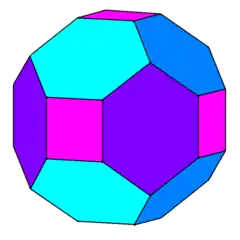
Le dodécaèdre rhombique tronqué est un polyèdre convexe obtenu par la troncature des six sommets du dodécaèdre rhombique où quatre faces se réunissent.
| Dodécaèdre rhombique tronqué | |
|---|---|
 | |
| Type | Quasi-solide de Johnson |
| Faces | 6 carrés 12 hexagones |
| Arêtes | 48 (2 types) |
| Sommets | 32 (2 types) |
| Configurations de sommets | (24) 4.6.6 (8) 6.6.6 |
| Groupe de symétrie | Oh |
| Polyèdre dual | - |
| Propriétés | Convexe, zonoèdre, faces hexagonales équilatérales mais non équiangles |
Les six sommets sont tronqués de façon que les arêtes soient de même longueur. Les douze faces rhombiques deviennent des hexagones, et les sommets tronqués deviennent des carrés.
Les faces hexagonales sont équilatérales, mais pas régulières, car elles ont des angles inégaux : deux angles opposés valent environ et les quatre autres valent environ 125,26°. (Les authentiques hexagones réguliers ont 120° à chaque angle.)
C'est un zonoèdre : toutes ses faces ont un centre de symétrie.
Patron
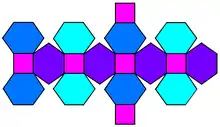
Ambiguïtés
Il ne faut pas confondre le dodécaèdre rhombique tronqué avec l'octaèdre tronqué, qui lui ressemble beaucoup :
Dodécaèdre rhombique tronqué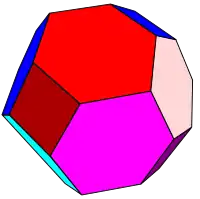 |
Octaèdre tronqué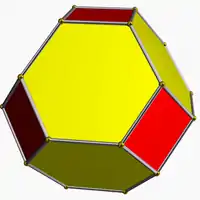 |
|---|
Malgré les apparences, et bien que convexe, le dodécaèdre rhombique tronqué n'est pas un solide de Johnson, car pas toutes ses faces sont strictement régulières ; c'est également le cas du triakitétraèdre tronqué et du triacontaèdre rhombique tronqué.
Le nom « dodécaèdre rhombique tronqué » est ambigu, car seulement six sommets ont été tronqués, or l'appellation « polyèdre tronqué » est généralement réservée aux polyèdres dont tous les sommets ont été tronqués. En tronquant les quatorze sommets d'un dodécaèdre rhombique, on obtient un tout autre polyèdre.
Mesures et volume

Si son arête a pour longueur ,
- son volume vaut :
- ;
- son aire est de :
- ;
- le rayon de la sphère passant par les centres des carrés vaut :
- ;
- le rayon de la sphère passant par les centres des hexagones vaut :
- .
Voir aussi
Article connexe
Liens externes
- VRML model
- VTML polyhedral generator Try "t4daC"
Crédit d'auteurs
- Portail de la géométrie