Vecteur vitesse angulaire

Le vecteur vitesse angulaire d'une particule au point P par rapport à l'origine O est déterminé par la composante orthogonale du vecteur vitesse v.

La vitesse angulaire d'une particule est mesurée par rapport ou relativement à un point, appelé origine. Comme indiqué sur la figure (avec les angles ${\displaystyle \phi }$ et ${\displaystyle \theta }$ en radians, si l'on trace une droite depuis l'origine (O) jusqu'à la particule (P), alors le vecteur vitesse (v) de la particule a une composante le long de la droite (composante radiale, v_∥) et une composante orthogonale (v_⊥). Si la composante radiale est nulle, la particule se déplace sur un cercle, alors que si la composante orthogonale est nulle, la particule se déplace sur une ligne droite passant par l'origine.

Un mouvement radial n'induit aucun changement dans la direction de la particule par rapport à l'origine, c'est pourquoi, lorsque l'on s'intéresse à la vitesse angulaire, la composante radiale peut être ignorée. Ainsi, la rotation est entièrement produite par le mouvement orthogonal relativement à l'origine, et la vitesse angulaire est entièrement déterminée par cette composante.

En deux dimensions, la vitesse angulaire ${\displaystyle \omega }$ est donnée par :

${\displaystyle \omega ={\frac {{\mathrm {d} }\phi }{{\mathrm {d} }t}}}$

Elle est reliée à la composante orthogonale de la vitesse par[1] :

${\displaystyle \mathrm {v} _{\perp }={|\mathrm {\mathbf {r} } |}\,{\frac {{\mathrm {d} }\phi }{{\mathrm {d} }t}}}$

Une formule explicite pour v_⊥ en fonction de v et ${\displaystyle \theta }$ est :

${\displaystyle \mathrm {v} _{\perp }=|\mathrm {\mathbf {v} } |\,\sin(\theta ).}$

En combinant les équations ci-dessus, on obtient une formule pour ${\displaystyle \omega }$:

${\displaystyle \omega ={\frac {|\mathrm {\mathbf {v} } |\sin(\theta )}{|\mathrm {\mathbf {r} } |}}.}$

En dimension 2, la vitesse angulaire est un nombre qui n'a pas de direction, mais qui a par contre un sens ou une orientation. C'est un pseudoscalaire, une quantité qui change de signe lorsqu'on effectue une opération de symétrie qui change l'orientation, c.-à-d. une inversion de parité (par exemple lorsqu'un des axes est inversé ou lorsqu'ils sont échangés). La direction positive de rotation est, par convention, lorsque l'on tourne depuis l'axe des x vers l'axe des y. Si l'on prend la convention inverse (donc si la parité est inversée), mais sans changer le sens de rotation de l'objet, alors le signe de la vitesse angulaire change.

Le vecteur vitesse angulaire décrit la vitesse de rotation et l'axe de rotation instantanée. La direction du vecteur vitesse angulaire est celle de l'axe de rotation ; dans ce cas (sens antihoraire) le vecteur pointe vers le haut

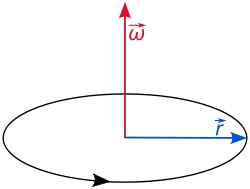
En trois dimensions, la vitesse angulaire devient un peu plus compliquée. La vitesse angulaire est en général considérée comme un vecteur, ou plus précisément, un pseudovecteur. On parle du vecteur (ou pseudovecteur) vitesse angulaire. Il a non seulement une magnitude, mais aussi une direction et un sens. La magnitude est la vitesse angulaire scalaire et la direction indique l'axe de rotation. Le sens du vecteur précise le sens de rotation, via la règle de la main droite.

Soit ${\displaystyle {\vec {u}}}$ un vecteur unitaire le long de l'axe instantané de rotation, orienté de telle sorte que, la rotation vue depuis la pointe du vecteur s'effectue dans le sens trigonométrique. Alors le vecteur vitesse angulaire ${\displaystyle {\vec {\omega }}}$ peut être défini par :

${\displaystyle {\vec {\omega }}={\frac {{\mathrm {d} }\phi }{{\mathrm {d} }t}}\cdot {\vec {u}}}$

Tout comme dans le cas de dimension 2, une particule a une composante de sa vitesse le long du rayon depuis l'origine vers la particule, et une autre composante orthogonale à ce rayon. La combinaison du rayon vecteur ${\displaystyle {\vec {r}}}$ et du vecteur vitesse ${\displaystyle {\vec {v}}}$ définit un plan de rotation (instantanée) dans lequel le mouvement de la particule (à cet instant) est simplement comme dans le cas de dimension 2. L'axe de rotation est une droite normale à ce plan, et cet axe définit la direction du pseudovecteur vitesse angulaire, alors que sa magnitude est la même que la grandeur pseudoscalaire obtenue dans le cas de dimension 2. En utilisant le vecteur unitaire ${\displaystyle {\vec {u}}}$ défini plus haut, on peut écrire le vecteur vitesse angulaire de manière similaire à celle du cas de la dimension 2 :

${\displaystyle {\vec {\omega }}={\frac {|\mathrm {\mathbf {v} } |\sin(\theta )}{|\mathrm {\mathbf {r} } |}}\,{\vec {u}}}$

ce qui, par définition du produit vectoriel, peut s'écrire :

${\displaystyle {\vec {\omega }}={\frac {{\vec {r}}\wedge {\vec {v}}}{|{\vec {r}}|^{2}}}}$

Il est possible de définir une opération d'addition de vecteurs vitesse angulaire en utilisant la composition des mouvements.

Si un point tourne avec une vitesse angulaire ${\displaystyle {\vec {\omega }}_{2}}$ dans un repère F₂ qui tourne lui-même avec une vitesse angulaire ${\displaystyle {\vec {\omega }}_{1}}$ par rapport à un repère extérieur F₁, on peut définir la somme ${\displaystyle \omega _{1}+\omega _{2}}$ comme étant le vecteur vitesse angulaire du point par rapport à F₁.

Avec l'opération d'addition définie ainsi, la vitesse angulaire, qui est un pseudovecteur, se comporte comme un vecteur usuel car il possède deux opérations :

• Une opération interne (addition) qui est associative, commutative, distributive et qui possède un élément neutre (le 0) et des éléments inverses (les opposés des vecteurs)
• Une opération externe (produit externe), la multiplication par un scalaire.

Avec ces deux opérations, l'ensemble des pseudovecteurs forment un espace vectoriel, malgré le nom pseudovecteurs qui pourrait suggérer le contraire. Les seules propriétés difficiles à prouver, sont la commutativité et l'associativité de l'addition. La commutativité par exemple, peut être prouvée en utilisant le fait que le tenseur de vitesse W (voir plus bas) est antisymétrique. De ce fait, R = \e^Wt est une matrice de rotation. Pour un temps dt, c'est une matrice de rotation infinitésimale, que l'on peut développer comme suit :

${\displaystyle \mathrm {R} =\mathrm {I} +\mathrm {W} \cdot \mathrm {d} t+{1 \over 2}(\mathrm {W} \cdot \mathrm {d} t)^{2}+\cdots }$

La composition des rotations n'est pas commutative, mais pour des rotations infinitésimales, on peut considérer l'approximation au premier ordre de la série ci-dessus, et on obtient

${\displaystyle (\mathrm {I} +\mathrm {W} _{1}\cdot \mathrm {d} t)(\mathrm {I} +\mathrm {W} _{2}\cdot \mathrm {d} t)=(\mathrm {I} +\mathrm {W} _{2}\cdot \mathrm {d} t)(\mathrm {I} +\mathrm {W} _{1}\cdot \mathrm {d} t)}$

et par conséquent :

${\displaystyle \omega _{1}+\omega _{2}=\omega _{2}+\omega _{1}}$.

Il est défini comme la vitesse angulaire de chacun des vecteurs du repère, de manière cohérente avec la définition générale.

On sait, grâce au théorème de rotation d'Euler que pour un repère tournant, il existe à chaque instant un axe instantané de rotation. Dans le cas d'un repère, le vecteur vitesse angulaire est le long de l'axe de rotation instantané.

Construction schématique de l'addition de vecteurs vitesse angulaire pour des repères tournants

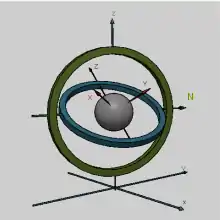
Comme dans le cas général, l'opération d'addition pour des vecteurs vitesse angulaire peut être définie en utilisant la composition des mouvements. Dans le cas de repères tournants, la composition des mouvements est plus simple que dans le cas général, car la matrice finale est toujours un produit de matrices de rotation.

Comme dans le cas général, l'addition est commutative ${\displaystyle {\vec {\omega }}_{1}+{\vec {\omega }}_{2}={\vec {\omega }}_{2}+{\vec {\omega }}_{1}}$.

On peut supposer que la base mobile ${\displaystyle B=({\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3})}$ est orthonormale directe (bien que cela ne soit pas indispensable). Il existe un vecteur ${\displaystyle {\vec {\omega }}}$ vérifiant ${\displaystyle {\dot {{\vec {e}}_{i}}}={\vec {\omega }}\times {\vec {e}}_{i}}$ dont les coordonnées dans cette base sont ${\displaystyle \omega _{1}={\dot {{\vec {e}}_{2}}}\centerdot {\vec {e}}_{3}}$, ${\displaystyle \,\omega _{2}={\dot {{\vec {e}}_{3}}}\centerdot {\vec {e}}_{1}}$, ${\displaystyle \,\omega _{3}={\dot {{\vec {e}}_{1}}}\centerdot {\vec {e}}_{2}}$.

On peut remarquer que ${\displaystyle {\dot {{\vec {e}}_{i}}}\centerdot {\vec {e}}_{j}=-{\dot {{\vec {e}}_{j}}}\centerdot {\vec {e}}_{i}}$ (les produits scalaires ${\displaystyle {\vec {e}}_{i}\centerdot {\vec {e}}_{j}}$ sont constants), ce qui permet de définir un tenseur antisymétrique d'ordre 2 ; le vecteur ${\displaystyle {\vec {\omega }}}$ est simplement son vecteur dual.

Diagramme montrant un repère d'Euler en vert

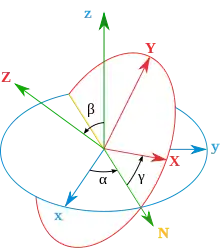
Les composantes du pseudovecteur vitesse angulaire ont été calculés pour la première fois par Leonhard Euler en utilisant ses angles d'Euler et un repère intermédiaire construit à partir des repères intermédiaires de la construction :

• Un axe du repère de référence (l'axe de précession)
• La ligne des nœuds du repère tournant par rapport au repère de référence (axe de nutation)
• Un axe du repère tournant (l'axe de rotation intrinsèque)

Euler prouva que les projections du pseudovecteur vitesse angulaire sur ces trois axes sont les dérivées des angles associés (ce qui est équivalent à décomposer la rotation instantanée en trois rotations de Euler instantanées). Ainsi[2]:

${\displaystyle \omega ={\dot {\alpha }}\mathbf {u} _{1}+{\dot {\beta }}\mathbf {u} _{2}+{\dot {\gamma }}\mathbf {u} _{3}}$