Voisinage (mathématiques)
En mathématiques, dans un espace topologique, un voisinage d'un point est une partie de l'espace qui contient un ouvert qui comprend ce point. C'est une notion centrale dans la description d'un espace topologique.
Pour les articles homonymes, voir Voisinage.
Par opposition aux voisinages, les ensembles ouverts permettent de définir élégamment des propriétés globales comme la continuité en tout point. En revanche, pour les propriétés locales comme la continuité en un point donné ou la limite, la notion de voisinage (et le formalisme correspondant) est plus adaptée.
En analyse réelle, l'utilisation des voisinages permet d'unifier le vocabulaire des limites finies et des limites infinies. Les voisinages dans un espace métrique permettent de généraliser la notion de limite à des espaces multidimensionnels. En analyse fonctionnelle, certaines des multiples notions de convergence pour une suite de fonctions nécessitent de dépasser le cadre des espaces métriques et de définir des voisinages sans recourir à une notion de distance.
Voisinage dans un espace topologique
Soit E un espace topologique et a un point de E. On dit que est un voisinage de a s'il existe un ouvert U de E tel que et . Notons alors l'ensemble des voisinages de a. Nous pouvons alors remarquer que :
- ;
- ;
- ;
- .
Nous pouvons ainsi affirmer que les voisinages de a forment un filtre sur E pour l'inclusion. On peut de plus remarquer que (comme un ouvert est voisinage de chacun de ses points) :
.
Topologie définie à partir des voisinages
La section précédente précise les propriétés des voisinages dans un espace topologique défini par sa famille d'ouverts. Il est toutefois possible de procéder de façon inverse : on peut définir une topologie en définissant l'ensemble des voisinages de chaque point pourvu que ceux-ci vérifient les axiomes suivants :
Soit E un ensemble. Nous dirons qu'une application forme un ensemble de voisinages si :
- 1. ;
- 2. ;
- 3. ;
- 4. ;
- 5. .
Il existe alors une (et une seule) topologie sur E telle que pour tout élément de E, soit l'ensemble des voisinages de pour cette topologie[1],[2].
Ces axiomes sont plus complexes que ceux qui régissent les ouverts. On les utilise parfois pour construire un espace topologique en ajoutant un point à un espace topologique déjà existant. C'est le cas notamment de la compactification d'Alexandrov. L'exemple ci-dessous de la droite numérique achevée est lui aussi traditionnel.
Base de voisinages
Les voisinages d'un point a dans un espace topologique E forment, on l'a vu, un filtre. On appelle système fondamental de voisinages de a, ou base de voisinages de a (pour cette topologie), une base de ce filtre, c'est-à-dire un ensemble B de voisinages de a tel que tout voisinage V de a contienne un élément U de B (c'est-à-dire que ), ou encore : un ensemble B de parties de E tel que les voisinages de a soient exactement les parties de E qui contiennent un élément de B[3].
Par exemple : les ouverts contenant a forment une base de voisinages de a. On peut même se limiter aux ouverts contenant a qui appartiennent à une base d'ouverts fixée.
Limite et continuité en un point
Le formalisme des voisinages permet d'exprimer simplement les notions de limite et de continuité en un point.
Limite
Soient E et F deux espaces topologiques, A une partie de E, f une application de A dans F, a un point de E adhérent à A et ℓ un point de F. On dit que ℓ est une limite de f au point a si pour tout voisinage V de ℓ, il existe un voisinage W de a tel que pour tout point x de W∩A, l'image f(x) appartient à V.
Il suffit pour cela que cette propriété soit vérifiée pour tout V d'une base de voisinages de ℓ.
Continuité
Soient E et F deux espaces topologiques, f une application de E dans F et a un point de E.
La fonction f est dite continue au point a si f(a) est une limite de f au point a, c'est-à-dire si l'image réciproque f−1(V) de tout voisinage V de f(a) est un voisinage de a.
Exemples
Le cas des nombres réels
Dans l'ensemble des réels muni de sa topologie usuelle, les intervalles ouverts forment une base d'ouverts. Pour tout réel a, les intervalles de la forme ]a – η, a + η[, quand η parcourt l'ensemble des réels strictement positifs, forment donc une base de voisinages de a. C'est un cas particulier des espaces métriques traités plus bas.
Exprimons alors la notion de limite, pour une fonction f définie sur un ensemble A de réels et à valeurs dans un espace topologique F (l'expression de la notion continuité s'en déduit immédiatement).
Soit a un réel adhérent à A. Un élément ℓ de F est une limite de f au point a si et seulement si, pour tout voisinage V de ℓ, il existe η > 0 tel que l'image de l'intersection de l'intervalle ]a – η, a + η[ avec A est incluse dans V. Formellement :
.
Dans le cas des fonctions réelles de la variable réelle, on obtient :.
Extension de la droite réelle
Dans la droite réelle achevée (l'ensemble ℝ = ℝ∪{−∞, +∞} muni de la topologie de l'ordre), une base de voisinages de +∞ (resp. −∞) est constituée des intervalles ]M, +∞] (resp. [−∞, M[) où M parcourt ℝ.
Si f est une application de A dans ℝ, où A est un ensemble de réels auquel +∞ est adhérent — c'est-à-dire que A n'est pas majoré dans ℝ — et si ℓ est un réel, on obtient les formulations classiques des limites en +∞ : ; ; .
Les formulations des limites en −∞ (si A n'est pas minoré) sont analogues.
Le cas des entiers positifs
Puisqu'une suite (un)n à valeurs dans un espace topologique F n'est rien d'autre qu'une application u de ℕ dans F et que ℕ est un ensemble non majoré de réels, on peut définir la notion de limite d'une suite comme cas particulier de celle de limite en +∞ d'une fonction de la variable réelle.
Traduire cette définition consiste à identifier, dans la topologie induite sur ℕ ∪ {+∞} par celle de ℝ, une base de voisinages de +∞ : ce sont les ensembles discrets ]M, +∞] ∩ (ℕ ∪ {+∞}) où M parcourt ℝ, autrement dit, les ensembles ([N, +∞[ ∩ ℕ) ∪ {+∞} où N parcourt ℕ.
Si par exemple la suite u = (un)n est à valeurs complexes, elle converge donc vers le complexe ℓ si et seulement si :
Remarque : dans cet espace compactifié « ℕ complété avec la valeur +∞ », les voisinages de +∞ sont les ensembles discrets S ∪ {+∞} où S parcourt le filtre de Fréchet, c'est-à-dire l'ensemble des parties de ℕ de complémentaire fini. Ce sont donc les mêmes voisinages que pour la topologie cofinie.
Espace métrique
Tout espace métrique est muni d'une topologie associée à la distance (voir le § « Définitions » de l'article sur les espaces métriques) : une base de cette topologie est constituée des boules ouvertes. Pour tout point a, les boules ouvertes contenant a forment donc une base de voisinages de a, et l'on peut même se limiter à celles qui sont centrées en a.
Exprimons alors la notion de limite pour une fonction entre espaces métriques. Soient (E, dE) et (F, dF) deux espaces métriques.
Soient A une partie de E, f une application de A dans F, a un point de E adhérent à A et ℓ un point de F. La fonction f a pour limite ℓ au point a si et seulement si pour tout ε > 0, il existe η > 0 tel que l'image de l'intersection de la boule B(a, η) avec A est incluse dans la boule B(ℓ, ε). Formellement :
.
Voisinage d'une partie
On dit qu'un ensemble V est un voisinage d'un ensemble S si V est un voisinage de tous les points de S ou encore, si V contient un ouvert contenant S.
Dans un espace métrique ,
- Pour tout sous-ensemble , et tout , l'ensemble est un voisinage ouvert de [4]. Si est compact, les ensembles forment un système fondamental de voisinages de [4].
- Un ensemble est appelé voisinage uniforme de s'il contient pour un certain . Une autre façon d'énoncer la propriété précédente est alors d'affirmer que tout voisinage d'un compact est uniforme.
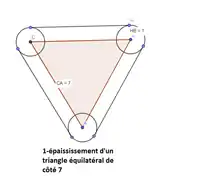
- Exemples
Notes et références
- Reformulation de N. Bourbaki, Éléments de mathématique, livre III : Topologie générale [détail des éditions], p. I.3, N° 2, proposition 2, où nos axiomes 2 et 3 sont regroupés en un seul : « Toute intersection finie de voisinages de a est un voisinage de a », avec la convention que dans ce contexte, l'intersection indexée par l'ensemble vide est E.
- Pour une démonstration, voir par exemple .
- Nawfal El Hage Hassan, Topologie générale et espaces normés, Dunod, , 2e éd. (lire en ligne), p. 5.
- Jean Dieudonné, Éléments d'analyse, t. I : Fondements de l'analyse moderne, Paris, Gauthier-Villars, (ISBN 978-2-04-010410-8, OCLC 489875029), p. 37, 64.
- Felice Ronga, « Analyse II », p. 25.
- Claude Tricot, Géométries et mesures fractales : une introduction, Ellipses, (ISBN 978-2-7298-4045-7 et 2-7298-4045-1, OCLC 37797645), p. 55 ou Claude Tricot, Courbes et dimension fractale, Springer, (lire en ligne), chap. 9., § 1, p. 109.
Voir aussi
Bibliographie
Laurent Schwartz, Topologie générale et analyse fonctionnelle, Hermann
Articles connexes
- Soit A une partie d'un espace topologique.
- Espace à bases dénombrables de voisinages
- Espace localement convexe
- Portail des mathématiques