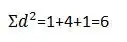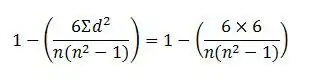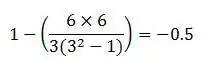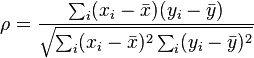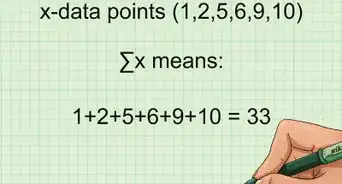How to Calculate Spearman's Rank Correlation Coefficient

Last Updated: February 17, 2023

Spearman's rank correlation coefficient allows you to identify whether two variables relate in a monotonic function (i.e., that when one number increases, so does the other, or vice versa). To calculate Spearman's rank correlation coefficient, you'll need to rank and compare data sets to find Σd², then plug that value into the standard or simplified version of Spearman's rank correlation coefficient formula. You can also calculate this coefficient using Excel formulas or R commands.

Things You Should Know

Calculate the coefficient by finding Σd², then plugging that value into the Spearman's rank correlation coefficient formula.
You can also easily calculate this coefficient using Excel.
Alternatively, you can find this coefficient using R commands.

Calculation Help

Sample Spearman's Rank Correlation Coefficient

Method 1

Method 1 of 3:

By Hand

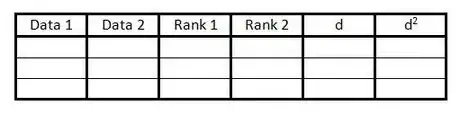
1
Draw your data table. This will organize the information you need to calculate Spearman's Rank Correlation Coefficient. You will need:^{[1]
X
Research source}
- 6 Columns, with headers as shown below.
- As many rows as you have pairs of data.
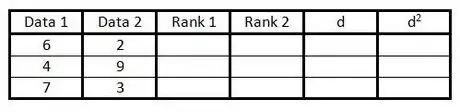
2
Fill in the first two columns with your pairs of data.

Advertisement
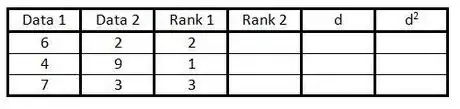
3
In your third column rank the data in your first column from 1 to n (the number of data you have). Give the lowest number a rank of 1, the next lowest number a rank of 2, and so on.
4
In your fourth column do the same as in step 3, but instead rank the second column.
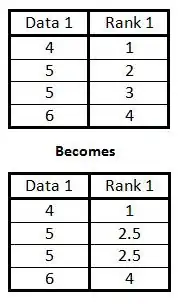
- If two (or more) pieces of data in one column are the same, find the mean of the ranks as if those pieces of data had been ranked normally, then rank the data with this mean.
  In the example at right, there are two 5s that would otherwise have ranks of 2 and 3. Since there are two 5s, take the mean of their ranks. The mean of 2 and 3 is 2.5, so assign the rank 2.5 to both 5s.
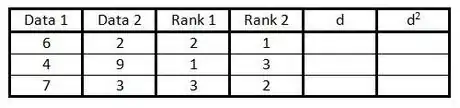
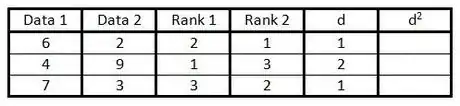
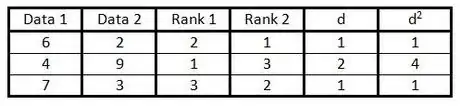
5
In the "d" column calculate the difference between the two numbers in each pair of ranks. That is, if one is ranked 1 and the other 3 the difference would be 2. (The sign doesn't matter, since the next step is to square this number.)^{[2]
X
Research source}
6
Square each of the numbers in the "d" column and write these values in the "d²" column.
7
Add up all the data in the "d²" column. This value is Σd².
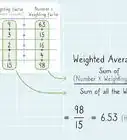
8
Choose one of these formulae:
- If there was no tie in previous steps, insert this value into the simplified Spearman's Rank Correlation Coefficient formula
  
  and replace the "n" with the number of pairs of data you have to calculate the answer.^{[3]
  X
  Research source}
- If there were ties in any of previous steps, use the standard Spearman's Rank Correlation Coefficient formula instead:
9
Interpret your result. It can vary between -1 and 1.
- Close to -1 - Negative correlation.
- Close to 0 - No linear correlation.
- Close to 1 - Positive correlation.

Method 2

Method 2 of 3:

In Excel

1
Create new columns with the ranks of your existing columns. For example, if your data is in Column A2:A11, you want to use the formula "=RANK(A2,A$2:A$11)", and copy it down and across for all your rows and columns.^{[4]
X
Research source}
2
Break ties as described in step 3, 4 method 1.
3
In a new cell, do a correlation between the two rank columns with something like "=CORREL(C2:C11,D2:D11)". In this case, C and D would correspond to the rank columns. The correlation cell will have your Spearman's Rank Correlation.

Method 3

Method 3 of 3:

Using R

1
Get R if you don't already have it. (See http://www.r-project.org.)
2
Save your data as a CSV file with the data you want to correlate in the first two columns. You can typically do this through the "Save as" menu.
3
Open the R editor. If you are on the terminal, simply run R. From the desktop, you want to click on the R logo.
4
Type the commands:
- d <- read.csv("NAME_OF_YOUR_CSV.csv") and hit enter
- cor(rank(d[,1]),rank(d[,2]))^{[5]
  X
  Research source}

Community Q&A

Question

How do I find coefficients?

Community Answer

The coefficient is next to the variable. With the example, "4pq," the coefficient is 4.
Question

Is there a correlation between data 1 and data 2?

Community Answer

No, there should not be a correlation.

Warnings

Spearman's rank correlation coefficient will only identify the strength of correlation where the data is consistently increasing or decreasing. If a scatter graph of the data any other trend Spearman's rank will not give an accurate representation of its correlation.

⧼thumbs_response⧽
Helpful 12 Not Helpful 7
This formula is based on the assumption that there are no ties. When there are ties such as in the example one should use the definition: the product moment correlation coefficient based on the ranks.

⧼thumbs_response⧽
Helpful 11 Not Helpful 8