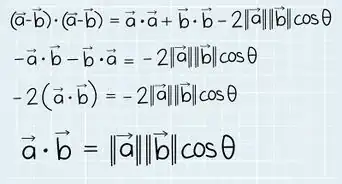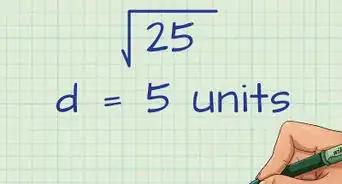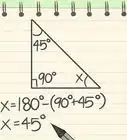How to Calculate the Cross Product of Two Vectors

Last Updated: January 31, 2023

The cross product is a type of vector multiplication only defined in three and seven dimensions that outputs another vector. This operation, used in almost exclusively three dimensions, is useful for applications in physics and engineering. In this article, we will calculate the cross product of two three-dimensional vectors defined in Cartesian coordinates.

Cheat Sheet

Cross Product of Vectors Diagram

Method 1

Method 1 of 2:

Calculating the Cross Product

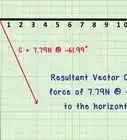
1
Consider two general three-dimensional vectors defined in Cartesian coordinates.^{[1]
X
Research source}
- ${\begin{aligned}\mathbf {a} &=A\mathbf {i} +B\mathbf {j} +C\mathbf {k} \\\mathbf {b} &=D\mathbf {i} +E\mathbf {j} +F\mathbf {k} \end{aligned}}$
- Here, $\mathbf {i} ,\mathbf {j} ,\mathbf {k}$ are unit vectors, and $A,B,C,D,E,F$ are constants.
2
Set up the matrix. One of the easiest ways to compute a cross product is to set up the unit vectors with the two vectors in a matrix.^{[2]
X
Research source}
- $\mathbf {a} \times \mathbf {b} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\A&B&C\\D&E&F\end{vmatrix}}$
Advertisement
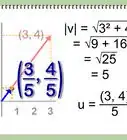
3
Calculate the determinant of the matrix. Below, we use cofactor expansion (expansion by minors).^{[3]
X
Research source}
- $\mathbf {a} \times \mathbf {b} =(BF-EC)\mathbf {i} -(AF-DC)\mathbf {j} +(AE-DB)\mathbf {k}$
- This vector is orthogonal to both $\mathbf {a}$ and $\mathbf {b} .$

Method 2

Method 2 of 2:

Example

1
Consider the two vectors below.
- ${\begin{aligned}\mathbf {u} &=2\mathbf {i} -\mathbf {j} +3\mathbf {k} \\\mathbf {v} &=5\mathbf {i} +7\mathbf {j} -4\mathbf {k} \end{aligned}}$
2
Set up the matrix.
- $\mathbf {u} \times \mathbf {v} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\2&-1&3\\5&7&-4\end{vmatrix}}$
3
Calculate the determinant of the matrix.
- ${\begin{aligned}\mathbf {u} \times \mathbf {v} &=(4-21)\mathbf {i} -(-8-15)\mathbf {j} +(14+5)\mathbf {k} \\&=-17\mathbf {i} +23\mathbf {j} +19\mathbf {k} \end{aligned}}$

Community Q&A

Question

How do I calculate the vector triple product?

Community Answer

Given vectors u, v, and w, the scalar triple product is u*(vXw). So by order of operations, first find the cross product of v and w. Set up a 3X3 determinant with the unit coordinate vectors (i, j, k) in the first row, v in the second row, and w in the third row. Evaluate the determinant (you'll get a 3 dimensional vector). Then dot that with u (to get a scalar). Inner products are abelian, so u*(vXw)=(vXw)*u. Interestingly, the absolute value of the T.S.P. yields the volume of a parallelpiped with 3 edges given by vectors u, v, and w.
Question

What is the vector analog of distance?

Community Answer

Norm, sometimes also called magnitude, generalizes distance to vectors. Norm is denoted with vertical bars like absolute values. For example, |(3,-4)| = 5, and |(1,1,1,1)| = 2.