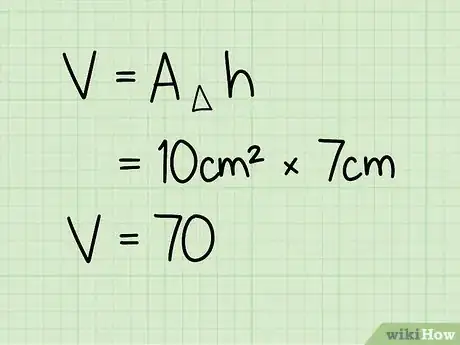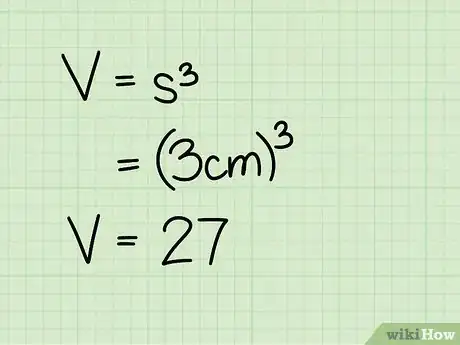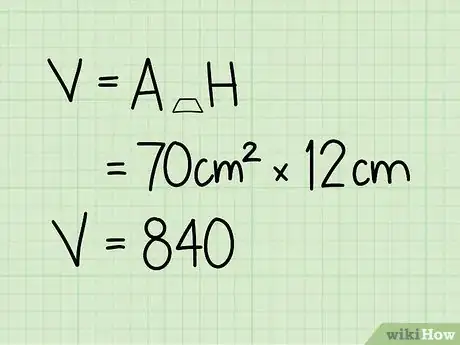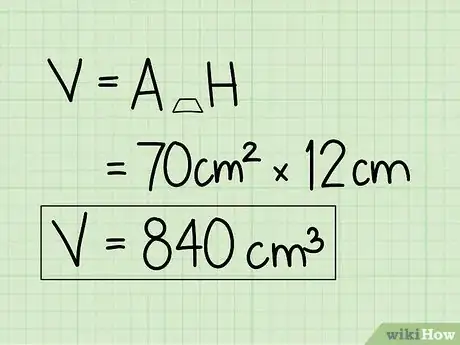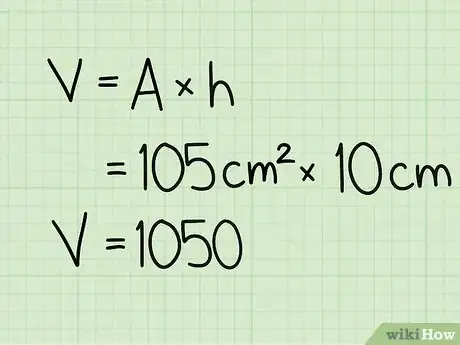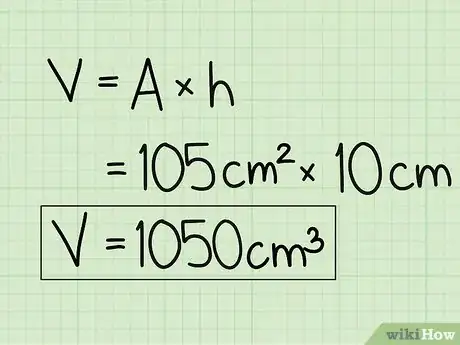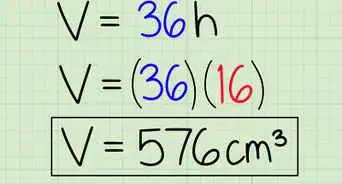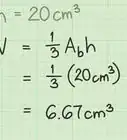How to Calculate the Volume of a Prism

A prism is a solid, multi-sided geometric figure with two identical ends called bases. To find the volume of a prism, first calculate the area of one of the bases, then multiply it by the height of the prism. You can choose either the top or the bottom base since the bases are parallel and congruent polygons, or identical 2-dimensional shapes. Volume is measured in cubic units — don’t forget to add units or your teacher might dock you some points. Read on for step-by-step instructions for calculating the volume of 5 different types of prisms.

Method 1
Method 1 of 5:

Calculating the Volume of a Triangular Prism

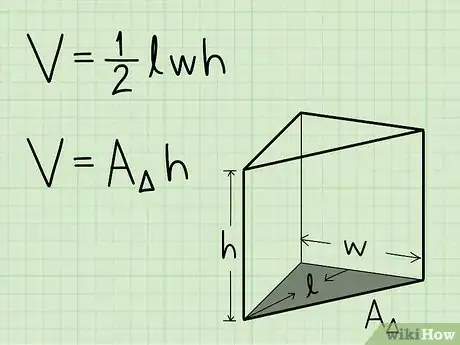
  1. Image titled Calculate the Volume of a Prism Step 1
    1
    Write down the formula for finding the volume of a triangular prism. The formula is simply V = 1/2 x length x width x height. However, we'll be taking this formula apart further to use the formula V = area of base x height. You can find the area of the base by using the formula for finding the area of a triangle -- multiplying 1/2 by the length and width of the base.[1]
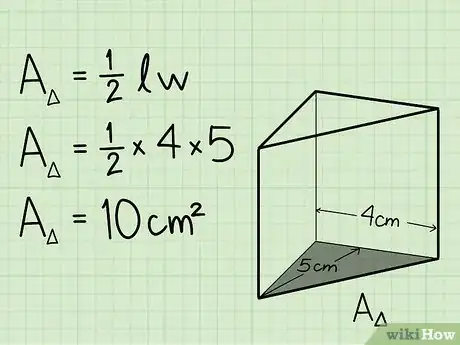
  2. Image titled Calculate the Volume of a Prism Step 2
    2
    Find the area of the base face. To calculate the volume of a triangular prism, you need to first find the area of the triangular base. Find the area of the base of the prism by multiplying 1/2 times the base of the triangle times its height.[2]
    • Ex: If the height of the triangular base is 5 cm and the base of the triangular prism is 4 cm, then the area of the base is 1/2 x 5 cm x 4 cm, which is 10 cm2.
    Advertisement
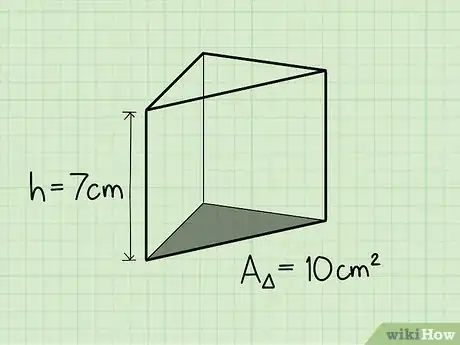
  3. Image titled Calculate the Volume of a Prism Step 3
    3
    Find the height. Let's say the height of this triangular prism is 7 cm.
  4. Image titled Calculate the Volume of a Prism Step 4
    4
    Multiply the area of the triangular base face times the height. Simply multiply the area of the base times the height. After you multiply the base and height, you'll have the volume of the triangular prism.[3]
    • Ex:10 cm2 x 7 cm = 70 cm3
  5. Image titled Calculate the Volume of a Prism Step 5
    5
    State your answer in cubic units. You should always use cubic units when you're calculating volume because you're working with three dimensional objects. The final answer is 70 cm.3
    6. Advertisement
Method 2
Method 2 of 5:

Calculating the Volume of a Cube

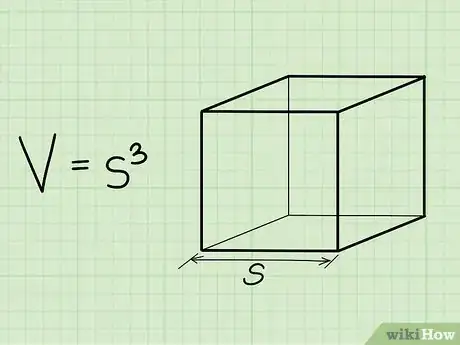
  1. Image titled Calculate the Volume of a Prism Step 6
    1
    Write down the formula for finding the volume of a cube. The formula is simply V = side3. A cube is a prism that happens to have three equal sides.[4]
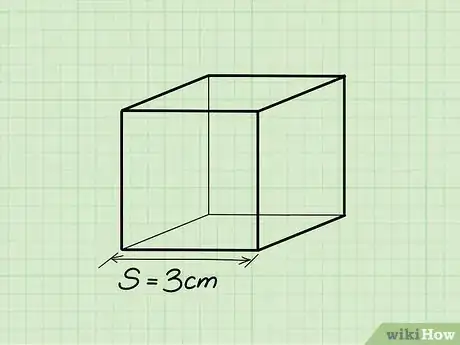
  2. Image titled Calculate the Volume of a Prism Step 7
    2
    Find the length of one side of the cube. All of the sides are equal, so it doesn't matter which side you choose.
    • Ex: Length = 3 cm.
  3. Image titled Calculate the Volume of a Prism Step 8
    3
    Cube it. To cube a number, just multiply it by itself twice. The cube of "a" is "a x a x a," for example. Since all of the lengths of the sides of the cube are equal, you don't have to find the area of the base and multiply it by the height and then multiply it by the length. Multiplying any two sides of the cube will give you the area of the base, and any third side could represent the height. You can still think of this as multiplying the length, width, and height when they all just happen to be the same.[5]
    • Ex: 3 cm3 = 3 cm. * 3 cm. * 3 cm. = 27 cm.3
  4. Image titled Calculate the Volume of a Prism Step 9
    4
    State your answer in cubic units. Don't forget to put your final answer in cubic units. The final answer is 27 cm.3
    5. Advertisement
Method 3
Method 3 of 5:

Calculating the Volume of a Rectangular Prism

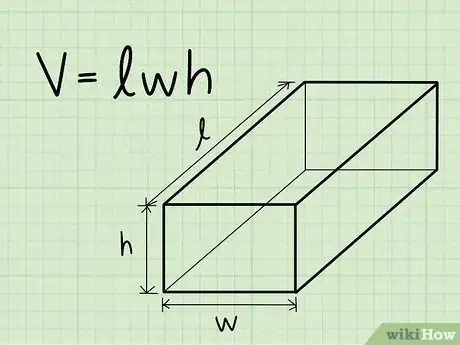
  1. Image titled Calculate the Volume of a Prism Step 10
    1
    Write down the formula for finding the volume of a rectangular prism. The formula is simply V = length * width * height. A rectangular prism is a prism with a rectangular base.[6]
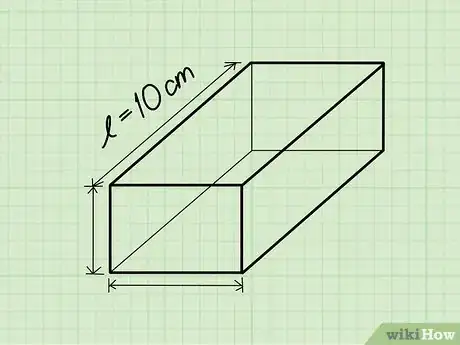
  2. Image titled Calculate the Volume of a Prism Step 11
    2
    Find the length. The length is the longest side of the flat surface of the rectangle on the top or bottom of the rectangular prism.
    • Ex: Length = 10 cm.
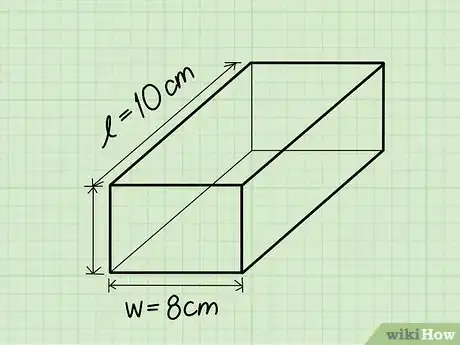
  3. Image titled Calculate the Volume of a Prism Step 12
    3
    Find the width. The width of the rectangular prism is the shorter side of the flat surface of the rectangle on the top or bottom of the shape.
    • Ex: Width = in 8 cm.
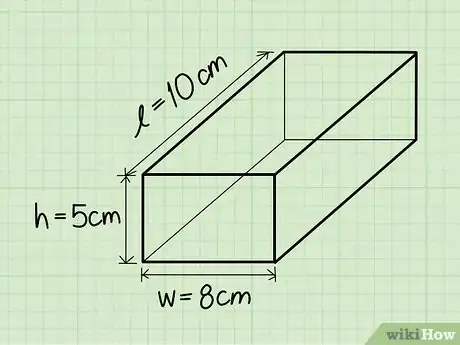
  4. Image titled Calculate the Volume of a Prism Step 13
    4
    Find the height. The height is the part of the rectangular prism that rises up. You can imagine the height of the rectangular prism as the part that stretches up a flat rectangle and makes it three-dimensional.
    • Ex: Height = 5 cm.
  5. Image titled Calculate the Volume of a Prism Step 14
    5
    Multiply the length, the width, and the height. You can multiply them in any order to get the same result. Using this method, you have essentially found the area of the rectangular base ( 10 x 8) and then have multiplied it by its height, 5. But to find the volume of this prism, you can multiply the lengths of the sides in any order.[7]
    • Ex: 10 cm. * 8 cm. * 5 cm = 400 cm.3
  6. Image titled Calculate the Volume of a Prism Step 15
    6
    State your answer in cubic units.[8] The final answer is 400 cm.3
    7. Advertisement
Method 4
Method 4 of 5:

Calculating the Volume of a Trapezoidal Prism

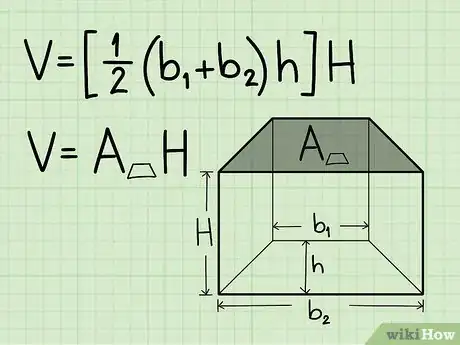
  1. Image titled Calculate the Volume of a Prism Step 16
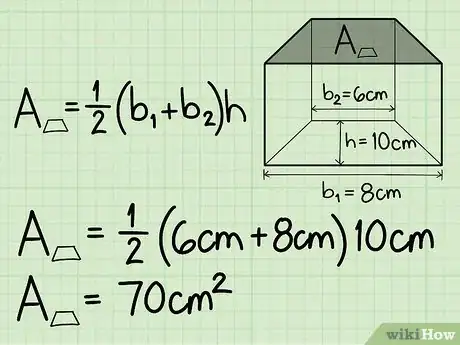
    1
    Write down the formula for calculating the volume of a trapezoidal prism. The formula is: V = [1/2 x (base1 + base2) x height] x height of the prism. You should use the first part of this formula to find the area of the trapezoidal base of the prism before you move forward.[9]
  2. Image titled Calculate the Volume of a Prism Step 17
    2
    Find the area of the trapezoidal base face. To do this, simply plug the two bases and the height of the trapezoidal base into the formula.
    • Let's say base 1 = 8 cm, base 2 = 6 cm, and height = 10 cm.
    • Ex: 1/2 x (6 + 8) x 10 = 1/2 x 14 cm x 10 cm = 70 cm2.
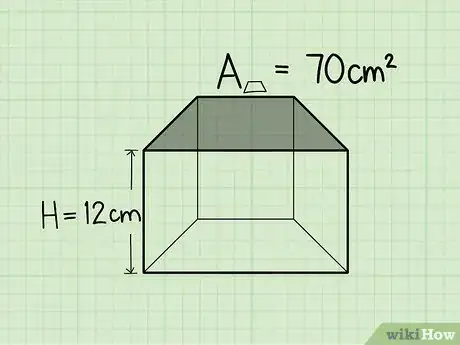
  3. Image titled Calculate the Volume of a Prism Step 18
    3
    Find the height of the trapezoidal prism. Let's say the height of the trapezoidal prism is 12 cm.
  4. Image titled Calculate the Volume of a Prism Step 19
    4
    Multiply the area of the base face times the height. To calculate the volume of the trapezoidal prism, just multiply the area of the base times the height.[10]
    • 70 cm2 x 12 cm = 840 cm3.
  5. Image titled Calculate the Volume of a Prism Step 20
    5
    State your answer in cubic units. The final answer is 840 cm3
    6. Advertisement
Method 5
Method 5 of 5:

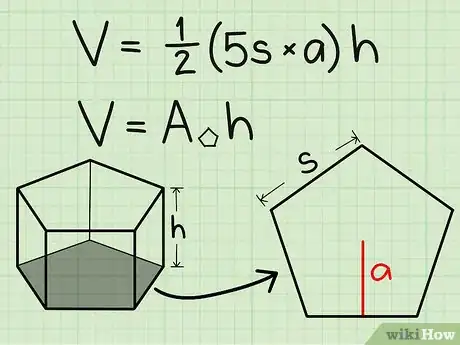
Calculating the Volume of a Regular Pentagonal Prism

  1. Image titled Calculate the Volume of a Prism Step 21
    1
    Write the formula for finding the volume of a regular pentagonal prism. The formula is V = [1/2 x 5 x side x apothem] x height of the prism. You can use the first part of the formula to find the area of the pentagonal base face. You can think of this as finding the area of the five triangles that make up a regular polygon. The side is simply the width of one triangle, and the apothem is the height of one of the triangles. You'll be multiplying by 1/2 because that's part of finding the area of a triangle and then multiplying this by 5 because 5 triangles make up the pentagon.[11]
    • For more information on finding the apothem if one is not provided for you, look here.[12]
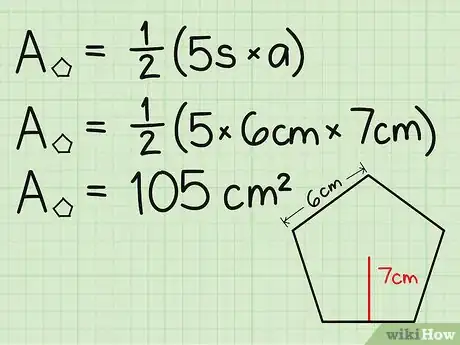
  2. Image titled Calculate the Volume of a Prism Step 22
    2
    Find the area of the pentagonal base face. Let's say the length of a side is 6 cm and the length of the apothem is 7 cm. Just plug these numbers into the formula:
    • A = 1/2 x 5 x side x apothem
    • A = 1/2 x 5 x 6 cm x 7 cm = 105 cm2
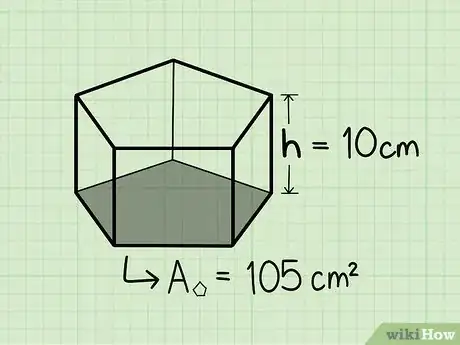
  3. Image titled Calculate the Volume of a Prism Step 23
    3
    Find the height. Let's say the height of the shape is 10 cm.
  4. Image titled Calculate the Volume of a Prism Step 24
    4
    Multiply the area of the pentagonal base face times the height. Just multiply the area of the pentagonal base, 105 cm2, times the height, 10 cm, to find the volume of the regular pentagonal prism.[13]
    • 105 cm2 x 10 cm = 1050 cm3
  5. Image titled Calculate the Volume of a Prism Step 25
    5
    State your answer in cubic units. The final answer is 1050 cm3.
    6. Advertisement

Community Q&A

  • Question
    How do I find the volume of rectangular prisms?
    Donagan
    Donagan
    Top Answerer
    Calculate the area of the base (length multiplied by width), then multiply by the height.
  • Question
    How do I calculate the volume of a rectangular prism if there are two different heights?
    Donagan
    Donagan
    Top Answerer
    A rectangular prism would not have two different heights. If you're asking about a non-rectangular prism, the volume formula would involve finding the average height of some of the sides.
  • Question
    How do I find the volume of a circular prism?
    Donagan
    Donagan
    Top Answerer
    The volume of a cylinder is found by squaring the radius and then multiplying by the product of pi and the height of the cylinder. (V = πr²h.)
Advertisement

You Might Also Like

Find Area
How to
Find Area
Calculate the Volume of a Pyramid
How to
Calculate the Volume of a Pyramid
Calculate the Volume of a Sphere
How to
Calculate the Volume of a Sphere
Find the Surface Area of a Rectangular Prism
How to
Find the Surface Area of a Rectangular Prism
Find the Surface Area of Cones
How to
Find the Surface Area of Cones
Calculate the Volume of a Cylinder
How to
Calculate the Volume of a Cylinder
Calculate the Volume of a Triangular Prism
How to
Calculate the Volume of a Triangular Prism
Calculate the Volume of a Rectangular Prism
How to
Calculate the Volume of a Rectangular Prism
Calculate Volume
How to
Calculate Volume
Calculate the Volume of a Cube
How to
Calculate the Volume of a Cube
Calculate the Volume of a ConeHow to Find the Volume of a Cone
Calculate Volume of a Box
How to
Calculate Volume of a Box
Calculate CBM
How to
Calculate CBM
Calculate the Volume of an Irregular Object
How to
Calculate the Volume of an Irregular Object
Advertisement

References

  1. ↑ https://www.bbc.co.uk/bitesize/guides/z26nb9q/revision/3
  2. ↑ https://virtualnerd.com/pre-algebra/perimeter-area-volume/volume/volume-examples/triangular-prism-volume-example
  3. ↑ https://www.omnicalculator.com/math/triangular-prism
  4. ↑ https://www.cuemath.com/measurement/volume-of-cube/
  5. ↑ https://www.omnicalculator.com/math/cube-volume
  6. ↑ https://www.khanacademy.org/math/cc-fifth-grade-math/5th-volume/volume-word-problems/a/volume-of-rectangular-prisms-review
  7. ↑ https://www.khanacademy.org/math/cc-fifth-grade-math/5th-volume/volume-word-problems/a/volume-of-rectangular-prisms-review
  8. ↑ https://www.omnicalculator.com/math/rectangular-prism-volume
  9. ↑ https://www.cuemath.com/geometry/trapezoidal-prism/
  1. ↑ https://www.cuemath.com/measurement/volume-of-trapezoidal-prism/
  2. ↑ https://www.cuemath.com/measurement/volume-of-pentagonal-prism/
  3. ↑ http://www.mathopenref.com/apothem.html
  4. ↑ https://www.volumecalc.com/volume-of-pentagonal-prism

About This Article

wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 47 people, some anonymous, worked to edit and improve it over time. This article has been viewed 664,301 times.
102 votes - 58%
Co-authors: 47
Updated: November 24, 2022
Views: 664,301
Categories: Volume
Article SummaryX

To find the volume of a triangular prism, use the equation V = ½ × length × width × height, or V = the area of the base × the height. Find the area of the base by multiplying ½ × the length and width of one of the triangular bases of the prism. Then, locate the height, and multiply the height by the area of the base. For example, a triangular prism with a length of 4 cm and a width of 5 cm would have an area of 10 cm^2. If the height was 7 cm, the volume of the prism would be 70 cm cubed. If you want to learn how to find the volume of a rectangular or pentagonal prism, keep reading the article!

Did this summary help you?
Advertisement