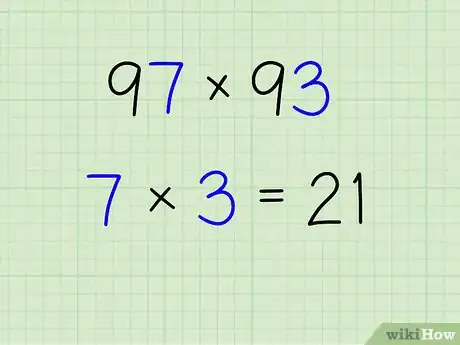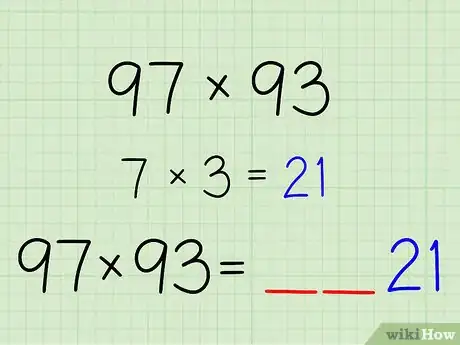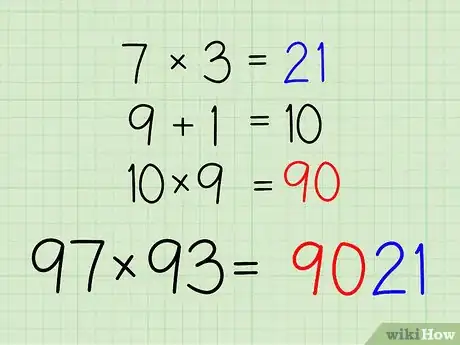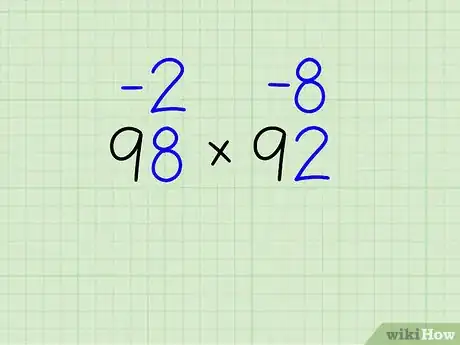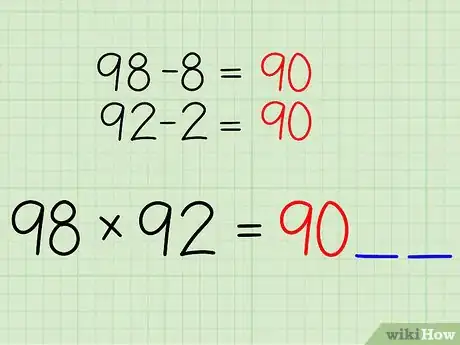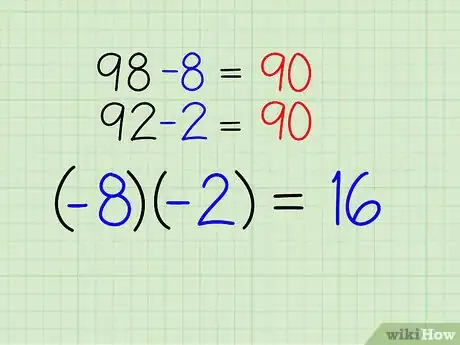X
wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 18 people, some anonymous, worked to edit and improve it over time.
This article has been viewed 205,462 times.
Learn more...
Vedic Math can be used to multiply large numbers in a matter of seconds without using a calculator! Here are some quick examples of how you can use this technique.
Steps
Part 1
Part 1 of 3:
Two-Digit Numbers
-
1Write the two digit numbers next to each other as so:
- 97 x 93
- Note: This example is for two-digit numbers that start with the same number and have second digits that equal 10 when added together (in this example, both numbers start with 9 and the second digits, 7 and 3, have a sum of 10).
-
2First, we multiply the two second digits together. In this case that would be:[1]
- 7 x 3 = 21
Advertisement -
3Place this result to the right-hand side of the final answer.
- Here you can see that the final answer will look like xx21
-
4Now add 1 to the first digit of the first number:
- 9 + 1 = 10
-
5Multiply 10 by the first digit of the second number:[2]
- 10 x 9 = 90
-
6Place this result on the left-hand side of the final answer, and you'll see that you have quickly calculated the correct answer to the original problem.
- 9021
Advertisement
Part 2
Part 2 of 3:
Two-Digit Numbers Alternate Method
-
1Take another set of two-digit numbers to be multiplied. Keep in mind that the first digits are the same and the sum of the second digits equals 10.
- 98 x 92
-
2Above each number, right the difference, or how deficient each of the numbers is from 100.[3]
- 98 is -2 from 100, so write -2 above 98
- 92 is -8 from 100, so write -8 above 92
-
3Cross-subtract these numbers from the value on the other side of the multiplication sign. You will see that it results in the same number.
- 98 - 8 = 90
- 92 - 2 = 90
-
4Place this number to the left-hand side of the final answer
- Now you can see that the final answer will look like 90xx
-
5Multiply the two differences together.[4]
- -2 x -8 = 16
-
6Place this number to the right-hand side of the final answer, and again see that you have quickly calculated the correct answer to the original problem.
- 9016
Advertisement
Part 3
Part 3 of 3:
Three Digit Numbers
-
1Take the two three-digit numbers to be multiplied and write as so:
- 104 x 103
-
2Now that we are above 100, right down how much higher each number is from 100.[5]
- 104 is +4 from 100, so write +4 above 104
- 103 is +3 from 100, so write +3 above 103
-
3Cross-add these numbers from the value on the other side of the multiplication sign. You will see that it results in the same number.
- 104 + 3 = 107
- 103 + 4 = 107
-
4Place this number to the left-hand side of the final answer.[6]
- Now you can see that the final answer will look like 107xx
-
5Multiply the two differences together.
- 4 x 3 = 12
-
6Place this number to the right-hand side of the final answer, and even here you'll be able see that you have quickly calculated the correct answer.
- 10712
Advertisement
Community Q&A
-
QuestionWhy do I cross-multiply them?
WOOHPCommunity AnswerTo simplify the answer to make it easier. -
QuestionDoes this apply to times 11 too?
FreyrTop AnswererYes, if the number multiplying by 11 was 19. The last digit of both numbers must add up to 10, and the first number must be equal on them.
Advertisement
References
- ↑ https://www.youtube.com/watch?v=PYrgjMubh-c
- ↑ https://www.youtube.com/watch?v=PYrgjMubh-c
- ↑ http://mathlearners.com/vedic-mathematics/multiplication-in-vedic-mathematics/
- ↑ http://mathlearners.com/vedic-mathematics/multiplication-in-vedic-mathematics/
- ↑ https://www.youtube.com/watch?v=7F0xtQ66dcg&feature=emb_logo
- ↑ https://www.youtube.com/watch?v=7F0xtQ66dcg&feature=emb_logo
About This Article
Advertisement
