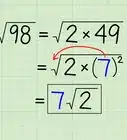This article was co-authored by wikiHow Staff. Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow's Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards.
There are 8 references cited in this article, which can be found at the bottom of the page.
This article has been viewed 35,404 times.
Learn more...
The difference of squares method is an easy way to factor a polynomial that involves the subtraction of two perfect squares. Using the formula , you simply need to find the square root of each perfect square in the polynomial, and substitute those values into the formula. The difference of squares method is a basic tool in algebra that you will likely use often when solving equations.
Steps
Evaluating the Polynomial
-
1Identify the coefficient, variable, and degree of each term. A coefficient is the number in front of a variable, which is multiplied by the variable.[1] The variable is the unknown value, usually denoted by or .[2] . The degree refers to the exponent of the variable. For example, a second-degree term has a value to the second power () and a fourth-degree term has a value to the fourth power ().[3]
- For example, in the polynomial , the coefficients are and , the variable is , and the first term () is a fourth-degree term, and the second term () is a second-degree term.
-
2Look for a greatest common factor. A greatest common factor is the highest factor that divides evenly into into two or more terms.[4] If there is a factor common to both terms of the polynomial, factor this out.[5]
- For example, the two terms in the polynomial have a greatest common factor of . Factoring this out, the problem becomes .
Advertisement -
3Determine whether the terms are perfect squares. If you factored out a greatest common factor, you are only looking at the terms that remain inside the parentheses. A perfect square is the result of multiplying an integer by itself.[6] A variable is a perfect square if its exponent is an even number.You can only factor using the difference of squares if each term in the polynomial is a perfect square.
- For example, is a perfect square, because . The number is also a perfect square, because . Thus, you can factor using the difference of squares formula.
-
4Make sure you are finding the difference. You know you are finding the difference if you have a polynomial that subtracts one term from another. The difference of squares only applies to these polynomials, and not those in which addition is used.
- For example, you cannot factor using the difference of squares formula, because in this polynomial you are finding a sum, not a difference.
Using the Formula
-
1Set up the formula for the difference of squares. The formula is . The terms and are the perfect squares in your polynomial, and and are the roots of the perfect squares.[7]
-
2Plug the first term into the formula. This is the value for . To find this value, take the square root of the first perfect square in the polynomial. Remember that a square root of a number is a factor you multiply by itself to get that number.[8]
- For example, since , the square root of is . So you should substitute this value for in the difference of squares formula: .
-
3Plug the second term into the formula. This is the value for , which is the square root of the second term in the polynomial.[9]
- For example, since , the square root of is . So you should substitute this value for in the difference of squares formula: .
-
4Check your work. Use the FOIL method to multiply the two factors. If your result is your original polynomial, you know you have factored correctly.[10]
- For example:
.
- For example:
Solving Practice Problems
-
1Factor this polynomial. Use the difference of two squares formula: .
- The terms have no greatest common factor, so there is no need to factor anything out of the polynomial.
- The term is a perfect square, since .
- The term is a perfect square, since .
- The difference of squares formula is . Thus, , where and are the square roots of the perfect squares.
- The square root of is . Plugging in for you have .
- The square root of is . So plugging in for , you have .
-
2Try factoring this polynomial. Make sure you factor out a greatest common factor, and use the difference of two squares: .
- Find the greatest common factor of each term. This term is , so factor this out of the polynomial: .
- The term is a perfect square, since .
- The term is a perfect square, since .
- The difference of squares formula is . Thus, , where and are the square roots of the perfect squares.
- The square root of is . Plugging in for you have .
- The square root of is . So plugging in for , you have .
-
3Factor the following polynomial. It has two variables, but it still follows the rules for the difference of squares method: .
- No factor is common to each term in this polynomial, so there is nothing to factor out before you begin factoring the difference of squares.
- The term is a perfect square, since .
- The term is a perfect square, since .
- The difference of squares formula is . Thus, , where and are the square roots of the perfect squares.
- The square root of is . Plugging in for you have .
- The square root of is . So plugging in for , you have .
References
- ↑ https://www.mathsisfun.com/definitions/coefficient.html
- ↑ http://www.mathsisfun.com/definitions/variable.html
- ↑ http://www.mathsisfun.com/algebra/degree-expression.html
- ↑ http://www.mathsisfun.com/definitions/greatest-common-factor.html
- ↑ https://virtualnerd.com/middle-math/number-theory-fractions/greatest-common-factor/greatest-common-factor-two-numbers-example
- ↑ http://www.mathwarehouse.com/arithmetic/numbers/what-is-a-perfect-square.php
- ↑ http://www.purplemath.com/modules/specfact.htm
- ↑ https://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut7_factor.htm
- ↑ https://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut7_factor.htm











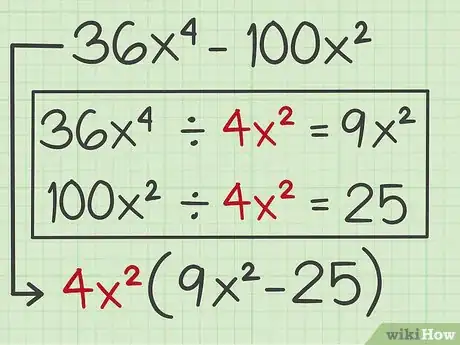


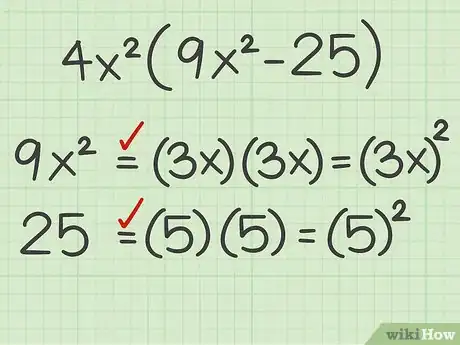





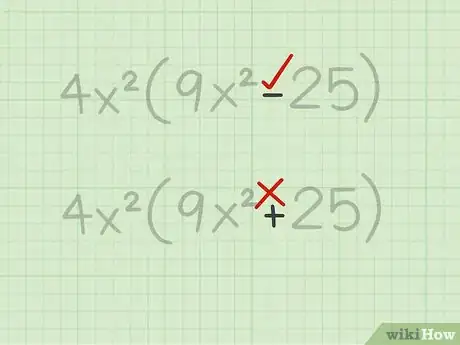






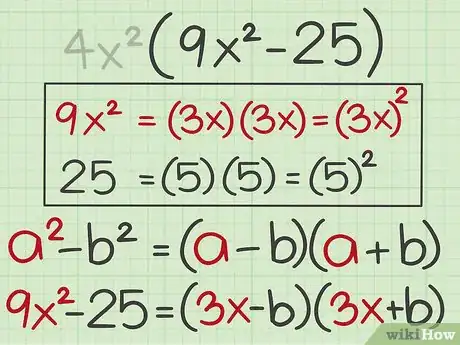


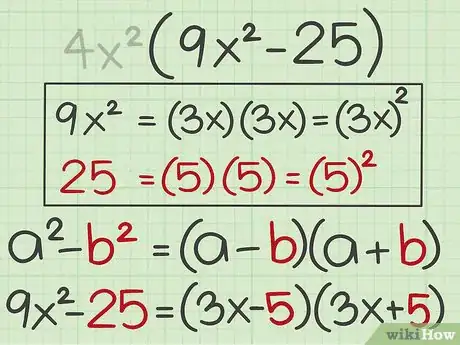


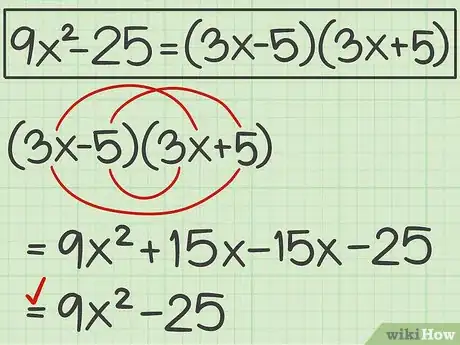



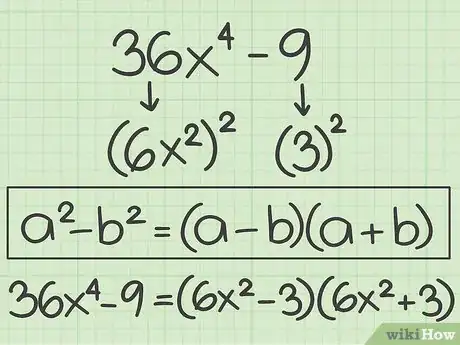









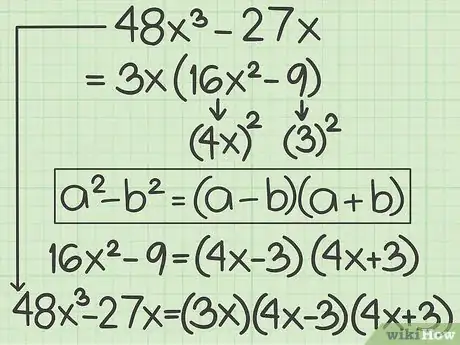








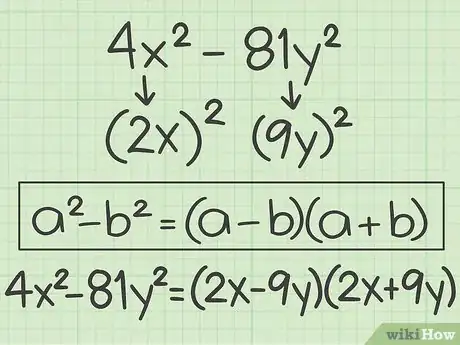









-Step-31-Version-2.webp)













-Step-31-Version-2.webp)