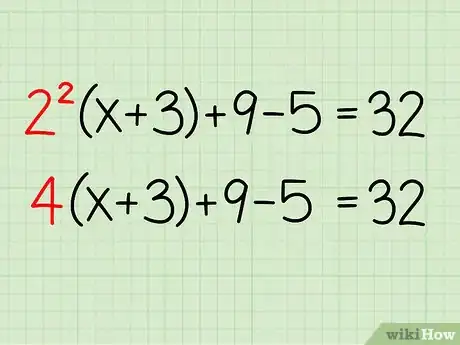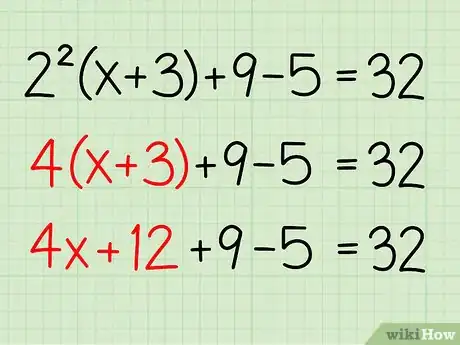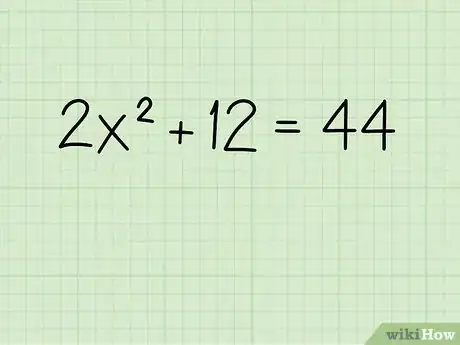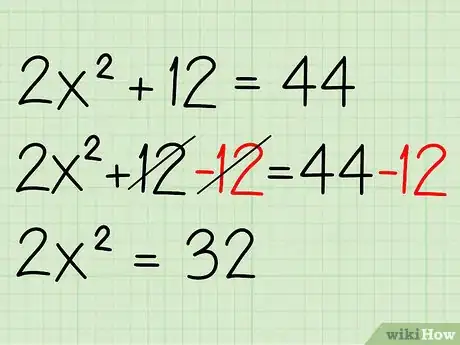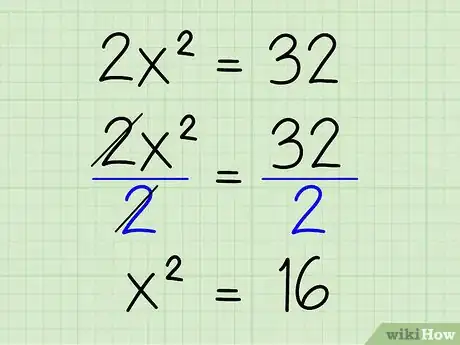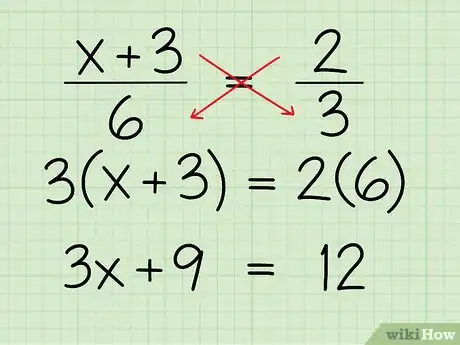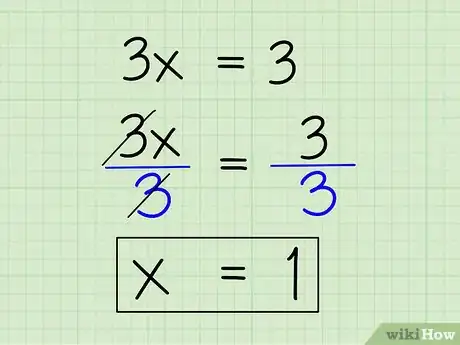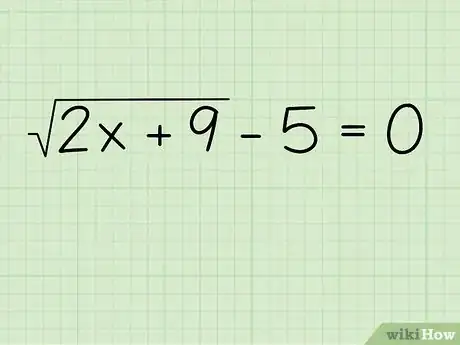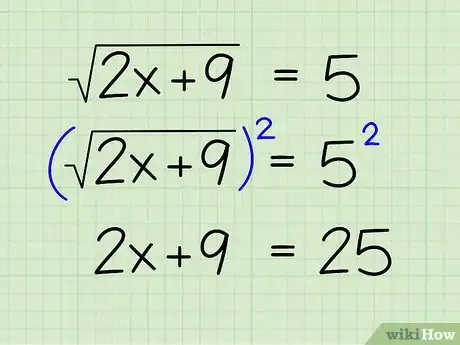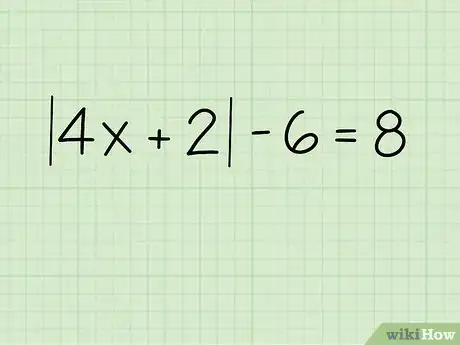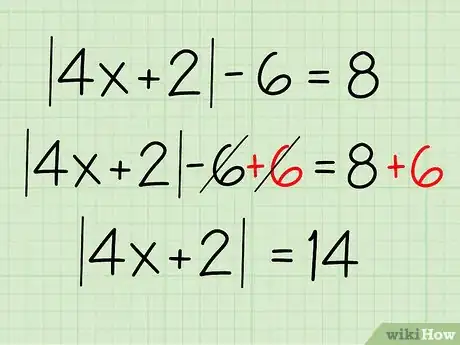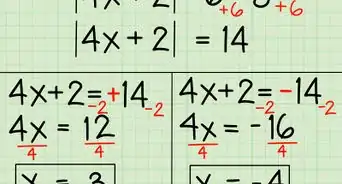How to Solve for X

There are a number of ways to solve for x, whether you're working with exponents and radicals or if you just have to do some division or multiplication. No matter what process you use, you always have to find a way to isolate x on one side of the equation so you can find its value. Here's how to do it:

Method 1
Method 1 of 5:

Using a Basic Linear Equation

  1. Image titled Solve for X Step 1
    1
    Write down the problem. Here it is:
    • 22(x+3) + 9 - 5 = 32
  2. Image titled Solve for X Step 2
    2
    Resolve the exponent. Remember the order of operations: PEMDAS, which stands for Parentheses, Exponents, Multiplication/Division, and Addition/Subtraction.[1] You can't resolve the parentheses first because x is in the parentheses, so you should start with the exponent, 22. 22 = 4
    • 4(x+3) + 9 - 5 = 32
    Advertisement
  3. Image titled Solve for X Step 3
    3
    Do the multiplication.[2] Just distribute the 4 into (x +3). Here's how:
    • 4x + 12 + 9 - 5 = 32
  4. Image titled Solve for X Step 4
    4
    Do the addition and subtraction. Just add or subtract the remaining numbers. Here's how:
    • 4x+21-5 = 32
    • 4x+16 = 32
    • 4x + 16 - 16 = 32 - 16
    • 4x = 16
  5. Image titled Solve for X Step 5
    5
    Isolate the variable.[3] To do this, just divide both sides of the equation by 4 to find x. 4x/4 = x and 16/4 = 4, so x = 4.
    • 4x/4 = 16/4
    • x = 4
  6. Image titled Solve for X Step 6
    6
    Check your work.[4] Just plug x = 4 back into the original equation to make sure that it checks out. Here's how:
    • 22(x+3)+ 9 - 5 = 32
    • 22(4+3)+ 9 - 5 = 32
    • 22(7) + 9 - 5 = 32
    • 4(7) + 9 - 5 = 32
    • 28 + 9 - 5 = 32
    • 37 - 5 = 32
    • 32 = 32
    7. Advertisement
Method 2
Method 2 of 5:

With Exponents

  1. Image titled Solve for X Step 7
    1
    Write down the problem. Let's say you're working with this problem where the x term includes an exponent:
    • 2x2 + 12 = 44
  2. Image titled Solve for X Step 8
    2
    Isolate the term with the exponent.[5] The first thing you should do is combine like terms so that all of the constant terms are on the right side of the equation while the term with the exponent is on the left side. Just subtract 12 from both sides. Here's how:
    • 2x2+12-12 = 44-12
    • 2x2 = 32
  3. Image titled Solve for X Step 9
    3
    Isolate the variable with the exponent by dividing both sides by the coefficient of the x term. In this case, 2 is the x coefficient, so divide both sides of the equation by 2 to get rid of it. Here's how:
    • (2x2)/2 = 32/2
    • x2 = 16
  4. 4
    Take the square root of each side of the equation.[6] Taking the square root of x2 will cancel it out. So, take the square root of both sides. You'll get x left over on one side and plus or minus the square root of 16, 4, on the other side. Therefore, x = ±4.
  5. 5
    Check your work. Just plug x = 4 and x = -4 back in to the original equation to make sure it checks out. For instance, when you're checking x=4:
    • 2x2 + 12 = 44
    • 2 x (4)2 + 12 = 44
    • 2 x 16 + 12 = 44
    • 32 + 12 = 44
    • 44 = 44
    6. Advertisement
Method 3
Method 3 of 5:

Using Fractions

  1. Image titled Solve for X Step 12
    1
    Write down the problem. Let's say you're working with the following problem:[7]
    • (x + 3)/6 = 2/3
  2. Image titled Solve for X Step 13
    2
    Cross multiply. To cross multiply, simply multiply the denominator of each fraction by the numerator of the other fraction.[8] You'll be essentially multiplying in two diagonal lines. So, multiply the first denominator, 6, by the second numerator, 2, to get 12 on the right side of the equation. Multiply the second denominator, 3, by the first numerator, x + 3, to get 3 x + 9 on the left side of the equation. Here's how it will look:
    • (x + 3)/6 = 2/3
    • 6 x 2 = 12
    • (x + 3) x 3 = 3x + 9
    • 3x + 9 = 12
  3. Image titled Solve for X Step 14
    3
    Combine like terms. Combine the constant terms in the equation to subtract 9 from both sides of the equation.[9] Here's what you do:
    • 3x + 9 - 9 = 12 - 9
    • 3x = 3
  4. Image titled Solve for X Step 15
    4
    Isolate x by dividing each term by the x coefficient. Just divide 3x and 9 by 3, the x term coefficient, to solve for x. 3x/3 = x and 3/3 = 1, so you're left with x = 1.[10]
  5. Image titled Solve for X Step 16
    5
    Check your work. To check your work, just plug x back in to the original equation to make sure that it works.[11] Here's what you do:
    • (x + 3)/6 = 2/3
    • (1 + 3)/6 = 2/3
    • 4/6 = 2/3
    • 2/3 = 2/3
    6. Advertisement
Method 4
Method 4 of 5:

Using Radical Signs

  1. Image titled Solve for X Step 17
    1
    Write down the problem. Let's say you're solving for x in the following problem:[12]
    • √(2x+9) - 5 = 0
  2. Image titled Solve for X Step 18
    2
    Isolate the square root. You have to move the part of the equation with the square root sign to one side of the equation before you can proceed. So, you'll have to add 5 to both sides of the equation. Here's how:
    • √(2x+9) - 5 + 5 = 0 + 5
    • √(2x+9) = 5
  3. Image titled Solve for X Step 19
    3
    Square both sides. Just as you would divide both sides of an equation by a coefficient that is being multiplied by x, you would square both sides of an equation if x appears under the square root, or the radical sign. This will remove the radical sign from the equation. Here's how you do it:
    • (√(2x+9))2 = 52
    • 2x + 9 = 25
  4. Image titled Solve for X Step 20
    4
    Combine like terms. Combine like terms by subtracting both sides by 9 so that all of the constant terms are on the right side of the equation while x remains on the left side. Here's what you do:
    • 2x + 9 - 9 = 25 - 9
    • 2x = 16
  5. Image titled Solve for X Step 21
    5
    Isolate the variable. The last thing you have to do to solve for x is to isolate the variable by dividing both sides of the equation by 2, the coefficient of the x term. 2x/2 = x and 16/2 = 8, so you're left with x = 8.
  6. Image titled Solve for X Step 22
    6
    Check your work. Plug 8 back in to the equation for x to see if you get the right answer:
    • √(2x+9) - 5 = 0
    • √(2(8)+9) - 5 = 0
    • √(16+9) - 5 = 0
    • √(25) - 5 = 0
    • 5 - 5 = 0
    7. Advertisement
Method 5
Method 5 of 5:

Using Absolute Value

  1. Image titled Solve for X Step 23
    1
    Write down the problem. Let's say you're trying to solve for x in the following problem:[13]
    • |4x +2| - 6 = 8
  2. Image titled Solve for X Step 24
    2
    Isolate the absolute value. The first thing you have to do is to combine like terms and get the terms inside the absolute value sign on one side. In this case, you would do it by adding 6 to both sides of the equation. Here's how:
    • |4x +2| - 6 = 8
    • |4x +2| - 6 + 6 = 8 + 6
    • |4x +2| = 14
  3. Image titled Solve for X Step 25
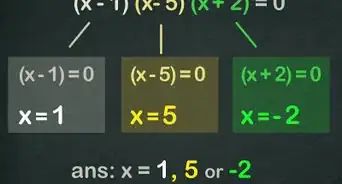
    3
    Remove the absolute value and solve the equation. This is the first and easiest step. You'll have to solve for x twice whenever you work with absolute value. Here's how you do it the first time:
    • 4x + 2 = 14
    • 4x + 2 - 2 = 14 -2
    • 4x = 12
    • x = 3
  4. Image titled Solve for X Step 26
    4
    Remove the absolute value and change the sign of the terms on the opposite side of the equal sign before you solve. Now, do it again, except set the first part of the equation equal to -14 instead of 14. Here's how:
    • 4x + 2 = -14
    • 4x + 2 - 2 = -14 - 2
    • 4x = -16
    • 4x/4 = -16/4
    • x = -4
  5. Image titled Solve for X Step 27
    5
    Check your work. Now that you know that x = (3, -4), just plug both numbers back in to the equation to see that it works. Here's how:
    • (For x = 3):
      • |4x +2| - 6 = 8
      • |4(3) +2| - 6 = 8
      • |12 +2| - 6 = 8
      • |14| - 6 = 8
      • 14 - 6 = 8
      • 8 = 8
    • (For x = -4):
      • |4x +2| - 6 = 8
      • |4(-4) +2| - 6 = 8
      • |-16 +2| - 6 = 8
      • |-14| - 6 = 8
      • 14 - 6 = 8
      • 8 = 8
    6. Advertisement

Practice Problems and Answers

Expert Q&A

  • Question
    What is the first step in solving for X?
    David Jia
    David Jia
    Math Tutor
    David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
    David Jia
    David Jia
    Math Tutor
    Expert Answer
    Start on the side of the equation with X and do the inverse operations to isolate X. For example, if the equation was X + 5 = 10, you would subtract 5 from each side.
  • Question
    How I solve this problem: 15 : 1000 : x : 100?
    Donagan
    Donagan
    Top Answerer
    If the problem is 15:1,000 = x:100, re-write it as one fraction equal to another: 15 / 1,000 = x / 100. Solve for x either by inspection or by cross-multiplication.
  • Question
    Solve for x; Peter is twice as old as his son. Twelve years ago he was four times older than him. How old are they now?
    Donagan
    Donagan
    Top Answerer
    Let x be the son's current age. Then 2x is Peter's current age. Twelve years ago the son's age was (x-12), and Peter's age was (2x-12). Set up an equation stating that Peter's age 12 years ago was four times the son's age then. Solve for x and 2x.
Advertisement

You Might Also Like

Find the Maximum or Minimum Value of a Quadratic Function Easily
How to
Find the Maximum or Minimum Value of a Quadratic Function Easily
Factor a Cubic Polynomial
How to
Factor a Cubic Polynomial
Algebraically Find the Intersection of Two Lines
How to
Algebraically Find the Intersection of Two Lines
Solve a Cubic Equation
How to
Solve a Cubic Equation
Simplify Radical Expressions
How to
Simplify Radical Expressions
Solve Systems of Algebraic Equations Containing Two Variables
How to
Solve Systems of Algebraic Equations Containing Two Variables
Calculate Frequency
How to
Calculate Frequency
Solve Quadratic Equations
How to
Solve Quadratic Equations
Complete the Square
How to
Complete the Square
Learn Algebra
How to
Learn Algebra
Find the Slope of an Equation
How to
Find the Slope of an Equation
Find a Number of Terms in an Arithmetic Sequence
How to
Find a Number of Terms in an Arithmetic Sequence
Solve an Algebraic Expression
How to
Solve an Algebraic Expression
Factor by Grouping
How to
Factor by Grouping
Advertisement

References

  1. ↑ David Jia. Academic Tutor. Expert Interview. 23 February 2021
  2. ↑ http://tutorial.math.lamar.edu/Classes/Alg/SolveLinearEqns.aspx
  3. ↑ https://www.purplemath.com/modules/solvelin.htm
  4. ↑ http://tutorial.math.lamar.edu/Classes/Alg/SolveLinearEqns.aspx
  5. ↑ https://sciencing.com/tips-for-solving-algebraic-equations-13712207.html
  6. ↑ https://sciencing.com/tips-for-solving-algebraic-equations-13712207.html
  7. ↑ https://www.youtube.com/watch?v=LMS1NR4gZN8
  8. ↑ https://www.mathsisfun.com/algebra/fractions-algebra.html
  9. ↑ https://www.youtube.com/watch?v=LMS1NR4gZN8
  1. ↑ https://www.youtube.com/watch?v=LMS1NR4gZN8
  2. ↑ https://www.youtube.com/watch?v=LMS1NR4gZN8
  3. ↑ http://www.mathsisfun.com/algebra/radical-equations-solving.html
  4. ↑ http://www.sosmath.com/algebra/solve/solve0/solve0.html

About This Article

David Jia
Co-authored by:
David Jia
Math Tutor
This article was co-authored by David Jia. David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math. This article has been viewed 674,662 times.
9 votes - 47%
Co-authors: 21
Updated: February 10, 2023
Views: 674,662
Categories: Algebra
Article SummaryX

To solve for x in a basic linear equation, start by resolving the exponent using the order of operations. Then, isolate the variable to get your answer. To solve for x when the equation includes an exponent, start by isolating the term with the exponent. Then, isolate the variable with the exponent by dividing both sides by the coefficient of the x term to get your answer. If the equation has fractions, start by cross-multiplying the fractions. Then, combine like terms and isolate x by dividing each term by the x coefficient. If you want to learn how to solve for x if the equation has radicals or absolute values, keep reading the article!

Did this summary help you?
Advertisement