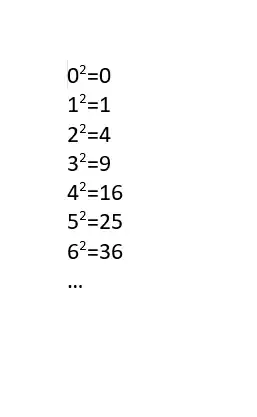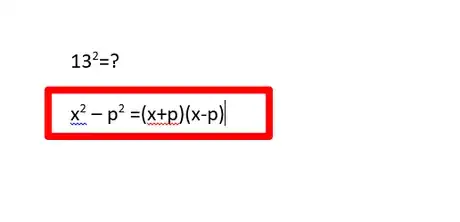How to Square Any Number

Last Updated: September 15, 2021 References

When given a number to square, sometimes it's tough to find the square of the answer - especially when learning some of this intermediate to advanced math for the first time. It'll become second nature and easier later, but you may be thinking "this sounds complicated". No need to worry - it isn't that bad. This article below will explain this procedure.

Method 1

Method 1 of 2:

Using Traditional Squaring Methods

1
Understand the meaning of squaring a number. When you square a number, you are essentially multiplying it by itself to form the product - or answer - to the multiplication problem.^{[1]
X
Research source}
- Learn the common squares of numbers so you don't have to do them repetitiously over and over again. All of the following can be solved using the format given below, however, sometimes people should (or may want to) memorize these facts so they don't need to run these problem again.
  - $0^{2}=0\times 0=0$
  - $1^{2}=1\times 1=1$
  - $2^{2}=2\times 2=4$
  - $3^{2}=3\times 3=9$
  - $4^{2}=4\times 4=16$
  - $5^{2}=5\times 5=25$
  - $6^{2}=6\times 6=36$
  - $7^{2}=7\times 7=49$
  - $8^{2}=8\times 8=64$
  - $9^{2}=9\times 9=81$
  - $10^{2}=10\times 10=100$
  - $11^{2}=11\times 11=121$
  - $12^{2}=12\times 12=144$
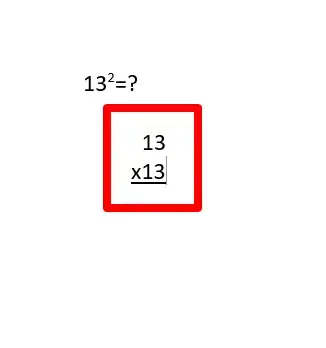
2
Use pencil and paper to write down the number you'd like to square. Dependent on where the final answer will be needed, the first few times you may need a "practice" page.

Advertisement
3
Write the same number below and expect to multiply them. If you need help, wikiHow has a guide on that too. Write number under number.
- Expect mistakes the first several times you end up having to use multiplication.
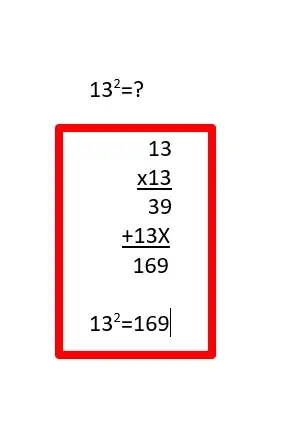
4
Multiply these numbers (called factors) using the format explained above. This type of multiplication solution solving is considered to have been solved using long multiplication.^{[2]
X
Research source}

Method 2

Method 2 of 2:

Utilizing Difference of Perfect Squares

1
Understand the difference of perfect squares shortcut. Shortcut to and write down the quick solution. Write down this trigger shortcut. The difference of two perfect squares states that when two squares are subtracted by one another the product of that number and another number when added (then subtracted) will equal your answer. This can be shown as $x^{2}-p^{2}=(x+p)(x-p)$ .^{[3]
X
Research source}
2
Find the value of $x^{2}$ . Evaluate what you know. Place the x value into the "equation" and add $p^{2}$ $p^{2}$ to both sides (cancels on the left side) will yield $x^{2}=(x+p)(x-p)+p^{2}$ $x^{2}=(x+p)(x-p)+p^{2}$ . Doing so, you'll be able to set up to capture your answer.^{[4]
X
Research source
Great Courses video series: Secrets of Mental Math, Episode 11:Advanced Mathematics}^{[5]
X
Research source}
- Build your factors and insert the values of the item you'd like to square into the formatted equation. Let x equal the number you'd like to find. Insert the number anywhere x is shown.
- Think about a number you could later insert for the p value. Consider making things easy and ensure the x value can be rounded up to the nearest 5 units, however, rounding it will work to any possible number. You don't want to think too far from the number.
3
Insert this number that you can add that will bring you into these common factor numbers into the p value in the equation.^{[6]
X
Research source}
4
Evaluate the much-smaller $p^{2}$ answer and add it to the equation in the place of the variable p.
5
Evaluate the equation. Add the x and p values, as well as subtracting them as the equation explains, then multiply those numbers together to get your product so far. Find the product to this part of the equation.^{[7]
X
Research source}
6
Add the product to this squared product for p. Find the sum of these two numbers. The sum will be the answer to the number squared.^{[8]
X
Research source}