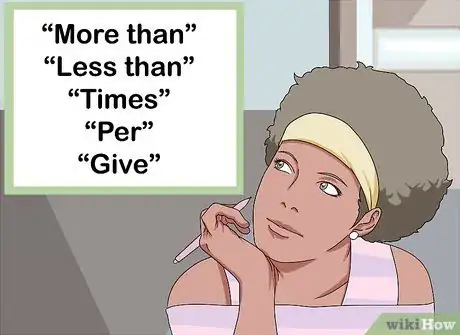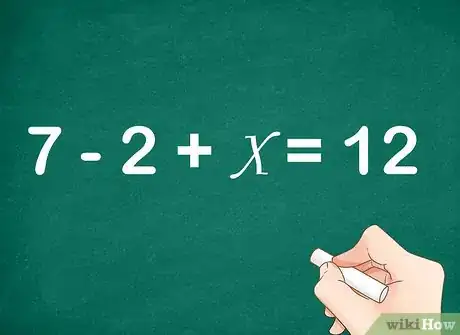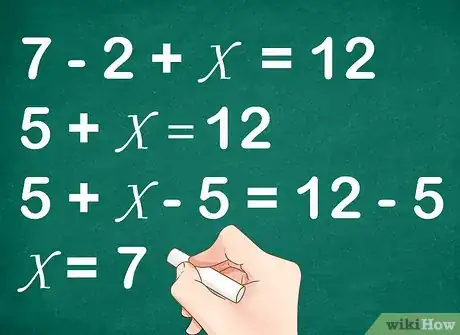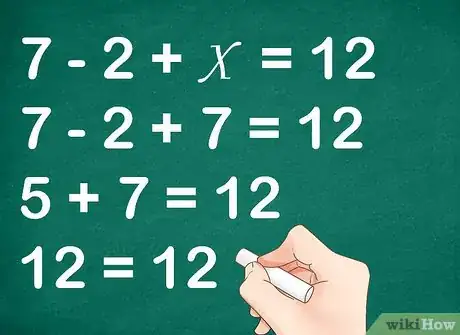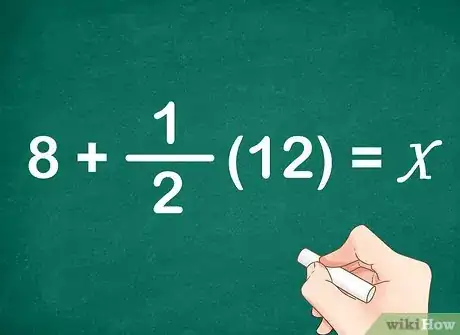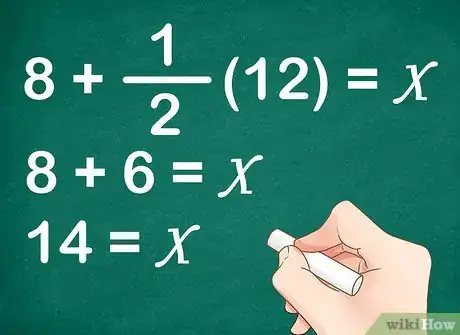How to Solve a Wordy Math Problem

Co-authored by Ronitte Libedinsky, MS

Last Updated: February 7, 2023 References

As your math skills advance, you will begin to encounter longer and longer word problems. Often these problems contain extraneous information that is not needed in order to solve the problem. These types of problem test your logic and math skills, as well as your reading comprehension and attention to detail. Solving these problems involves the same steps you would use to solve any problem, except more care is needed to consider and assess which information is important and which information is not.

Part 1

Part 1 of 3:

Understanding the Problem

$Image titled Solve a Wordy Math Problem Step 1$

1
Be organized. Wordy math problems can be convoluted, so you need to approach them with an organized mind and work space. Give yourself plenty of room to take notes, and write your words and numbers clearly.
- It might be helpful to box out a work space where you do your calculations. Then, write any conclusions or information in a different box where you have room to keep them organized. Using tables and bubble maps can be helpful. Use whatever organizational methods work best for you.
$Image titled Solve a Wordy Math Problem Step 2$

2
Read the entire problem. Don’t assume that you know what the problem is asking. Wordy math problems can be very misleading, and if you don’t read all of the information, you can be easily tricked.
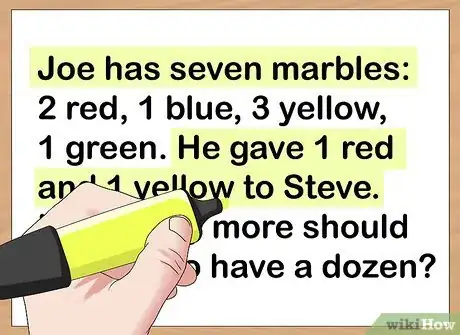
- For example, you might have the following problem: Joe has 7 marbles: 2 red, 1 blue, 3 yellow, and 1 green. He gave 1 red and 1 yellow to Steve. How many more marbles should Joe buy to have a dozen marbles?
- If you did not read the entire problem above, you might assume the problem was asking how many marbles Joe had after giving 2 marbles to Steve. But the problem is asking a very different question.
Advertisement
$Image titled Solve a Wordy Math Problem Step 3$

3
Read slowly. The writers of wordy math problems are trying to confuse you by cramming a lot of information into the problem. Sometimes this information is relevant; sometimes it isn’t. To understand what to do with all of the information you are given, it’s best to read the problem sentence-by-sentence. Pause after you read each piece of information to fully process what you have read.^{[1]
X
Research source}
- Reading slowly will prevent you from being overwhelmed, as well as make it easier to sift the relevant facts from the problem.
$Image titled Solve a Wordy Math Problem Step 4$

4
Find the question. After reading the problem carefully, locate what the problem is asking you to find.^{[2]
X
Expert Source

Ronitte Libedinsky, MS
Academic Tutor
Expert Interview. 26 May 2020.} Often this information will be at the end of the problem, in the form of a question, but not always.^{[3]
X
Research source} Underline the question so that you can easily refer back to it will working through the problem.
- For example, underline the sentence: “How many more marbles should Joe buy to have a dozen marbles?”
$Image titled Solve a Wordy Math Problem Step 5$

5
Cross out unnecessary information. For problems that are very wordy, you will likely come across information that is not necessary for answering the question. Re-read the problem and cross out this information. This will make the information and steps you need to solve the problem easier to parse.
- Be absolutely certain that information is unnecessary before crossing it out.
- It might also help to consolidate information. For example, if the problem describes the parts or components of a whole, but all you need to know is information about the whole, cross out the information about the parts and write in what those parts add up to.
- For example, it is irrelevant to know that Joe had 2 red, 1 blue, 3 yellow, and 1 green marble. All that is important is that he had 7 marbles. It is also irrelevant that 1 of the marbles he gave Steve was red and 1 was orange. All you need to know is that he gave Steve 2 marbles.
$Image titled Solve a Wordy Math Problem Step 6$

6
Highlight important information. Highlighting important information makes it easier to reference as you solve. You can also rewrite this information to make it clearer.
- For example, you can highlight the phrases “Joe has 7 marbles” and “He gave Steve 2.”
$Image titled Solve a Wordy Math Problem Step 7$

7
Draw a picture. Visualize what is happening in the word problem. Then, draw a picture or diagram that represents the known information.^{[4]
X
Research source} This will help you determine which information is unknown, and what steps you can take to find out this information.
- For example, in one color, draw Joe’s 7 marbles. Then, cross out the 2 he gives to Steve. Finally, in another color, draw more marbles until the amount is equal to 12.
$Image titled Solve a Wordy Math Problem Step 8$

8
Label graphs and diagrams clearly. If these are included with the problem, they will likely already be labeled. Make sure you understand what each piece of information means. Check the graph against the word problem to understand how each piece of information is represented in the graph.
- If you drew your own graph or diagram, label it clearly now, so that you are not confused when you use it later to help you solve the problem.

Advertisement

Part 2

Part 2 of 3:

Solving the Problem

$Image titled Solve a Wordy Math Problem Step 9$

1
Look for keywords and key phrases. Highlighting these in the problem will help you translate the written words into math. Specifically, keywords can give you clues about which operations to use in order to find the answer.^{[5]
X
Research source} For example:
- Phrases that indicate addition include “more than,” “total of,” and “added to.”^{[6]
  X
  Research source}
- Phrases that indicate subtraction include “decreased by,” “difference between,” and “less than.”^{[7]
  X
  Research source}
- Words that indicate multiplication include “of” and “times.”^{[8]
  X
  Research source}
- Words that indicate division include “per” and “out of.”^{[9]
  X
  Research source}
- In the sample problem, you would highlight the word “give,” which denotes subtraction. You would also highlight the phrase “how many more,” which suggests addition.
$Image titled Solve a Wordy Math Problem Step 10$

2
Assign variables to unknown information. Word problems that ask for a specific quantity will usually only have one unknown, but if the word problem is asking for an equation, you might have multiple unknowns, and therefore multiple variables. A variable can be any letter or symbol.^{[10]
X
Research source}
- For example, let $x$ equal the number of marbles Joe needs to buy to have a dozen (12) marbles.
$Image titled Solve a Wordy Math Problem Step 11$

3
Write an equation. Think about the known information, unknown information, what you are trying to find, and how you can find it. Use the keywords and key phrases to translate the English into an algebraic equation.^{[11]
X
Expert Source

Ronitte Libedinsky, MS
Academic Tutor
Expert Interview. 26 May 2020.}
- For example, you know that Joe begins with 7 marbles, gives away 2, adds an unknown amount, and ends up with 12. So, your equation will be $7-2+x=12$ .
$Image titled Solve a Wordy Math Problem Step 12$

4
Use algebra to solve. To find the value of a variable, you need to isolate the variable on one side of the equation. Follow the regular rules of algebra to do this, and remember to keep the equation balanced. This means that whatever you do to one side of the equation, you must also do to the other side.
- For example, to find the value of $x$ in the equation $7-2+x=12$ , you would calculate:
  $7-2+x=12$
  $5+x=12$
  $5+x-5=12-5$
  $x=7$
  So, Joe needs to buy 7 marbles to have a dozen.
$Image titled Solve a Wordy Math Problem Step 13$

5
Check your work. Make sure that your answer is reasonable.^{[12]
X
Research source} You should also plug the value of the variable back into the equation to verify that it makes the equation true.^{[13]
X
Research source} If your answer does not seem correct, follow all the steps again to check where you went wrong.
- For example, since Joe only wants 12 marbles, it is reasonable that he would need to buy 7. Substituting your solution for the variable, you would calculate:
  $7-2+x=12$
  $7-2+7=12$
  $5+7=12$
  $12=12$
  Since this is true, you know your solution is correct.

Advertisement

Part 3

Part 3 of 3:

Solving a Sample Problem

$Image titled Solve a Wordy Math Problem Step 14$

1
Solve the following problem. Bella has 48 colored pencils. Eight of her pencils are primary colors. Another 8 are secondary colors. The rest of the pencils are tertiary colors. She gets 12 more colored pencils for her birthday. Half of these pencils are primary colors. How many primary colored pencils does she have all together?
$Image titled Solve a Wordy Math Problem Step 15$

2
Read slowly and find the question.^{[14]
X
Expert Source

Ronitte Libedinsky, MS
Academic Tutor
Expert Interview. 26 May 2020.}Don’t stress out about extraneous information that you might not understand. For example, you don’t need to know what a primary, secondary, or tertiary color is in order to solve this problem. In this problem, the question comes in the last sentence: How many primary colored pencils does Bella have now? So, you only need to worry about how many primary colors Bella has all together; you don’t need to know what a primary color is.
- If you get overwhelmed, break the problem up into chunks and go one step at a time.^{[15]
  X
  Expert Source
  
  Ronitte Libedinsky, MS
  Academic Tutor
  Expert Interview. 26 May 2020.}
$Image titled Solve a Wordy Math Problem Step 16$

3
Assess which information is important, and which isn’t. It is not important to know that Bella begins with 48 total pencils. Since you are asked to find the number of primary pencils she has, it is only important to know that she begins with 8 primary pencils. It is also important to know that half of the 12 pencils she gets for her birthday are also primary colors. It is not important to know how many of her pencils are secondary or tertiary colors.
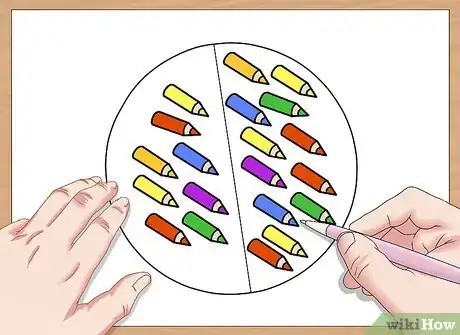
$Image titled Solve a Wordy Math Problem Step 17$

4
Draw a picture. For this problem, you might draw 8 colored pencils in one group. Then, draw 12 colored pencils in another group. Draw a circle that encompasses the group of 8, and half of the group of 12.
$Image titled Solve a Wordy Math Problem Step 18$

5
Look for keywords.^{[16]
X
Expert Source

Ronitte Libedinsky, MS
Academic Tutor
Expert Interview. 26 May 2020.} The phrase “half of” indicates that something will be multiplied by ${\frac {1}{2}}$ (or divided by 2). The phrase “all together” indicates that addition will be involved.
$Image titled Solve a Wordy Math Problem Step 19$

6
Assign variables and write an equation. The unknown information is how many primary colored pencils Bella has altogether. So, let the variable $x$ stand for this quantity. We know that she begins with 8 primary pencils, and that when she is given 12 more colored pencils, half of them are also primary. Thus, the equation would be $8+{\frac {1}{2}}(12)=x$ .
$Image titled Solve a Wordy Math Problem Step 20$

7
Solve and check your work. For the equation you would first find half of 12, and then add:
$8+{\frac {1}{2}}(12)=x$
$8+6=x$
$14=x$ So, altogether, 14 of Bella’s pencils are primary colors. To check, consider whether this answer is reasonable. Since Bella begins with 8 primary colored pencils, and is given less than 12 more, it seems reasonable that she would end up with 14 primary colored pencils.

Advertisement

Expert Q&A

Question

How do you solve a word problem being calm?

Ronitte Libedinsky, MS
Academic Tutor
Ronitte Libedinsky is an Academic Tutor and the Founder of Brighter Minds SF, a San Francisco, California based company that provides one-on-one and small group tutoring. Specializing in tutoring mathematics (pre-algebra, algebra I/II, geometry, pre-calculus, calculus) and science (chemistry, biology), Ronitte has over 10 years of experience tutoring to middle school, high school, and college students. She also tutors in SSAT, Terra Nova, HSPT, SAT, and ACT test prep. Ronitte holds a BS in Chemistry from the University of California, Berkeley, and an MS in Chemistry from Tel Aviv University.

Ronitte Libedinsky, MS

Academic Tutor

Expert Answer

Break the word problem down into chunks so you don't get overwhelmed. Just go step-by-step. Also, look for keywords that tell you what the word problem is looking for. For instance, "half of" means dividing by 2, and "all together" means adding.
Question

The tens digit and the ones digit of a certain number are equal. If the sum of the digits of the number is 50, what is the number?

Donagan

Top Answerer

This problem cannot be solved without additional information such as how many digits there are in the number.

Advertisement

You Might Also Like

Advertisement

References

↑ http://www.manyagroup.com/blog/how-to-approach-wordy-math-questions-on-the-new-sat/
↑ Ronitte Libedinsky, MS. Academic Tutor. Expert Interview. 26 May 2020.
↑ http://www.algebralab.org/lessons/lesson.aspx?file=Algebra_OneVariableWritingEquations.xml
↑ http://www.ldonline.org/article/62401/
↑ http://www.purplemath.com/modules/translat.htm
↑ http://www.purplemath.com/modules/translat.htm
↑ http://www.purplemath.com/modules/translat.htm
↑ http://www.purplemath.com/modules/translat.htm
↑ http://www.purplemath.com/modules/translat.htm

More References (7)

↑ http://www.algebralab.org/lessons/lesson.aspx?file=Algebra_OneVariableWritingEquations.xml
↑ Ronitte Libedinsky, MS. Academic Tutor. Expert Interview. 26 May 2020.
↑ http://www.ldonline.org/article/62401/
↑ http://www.algebralab.org/lessons/lesson.aspx?file=Algebra_OneVariableWritingEquations.xml
↑ Ronitte Libedinsky, MS. Academic Tutor. Expert Interview. 26 May 2020.
↑ Ronitte Libedinsky, MS. Academic Tutor. Expert Interview. 26 May 2020.
↑ Ronitte Libedinsky, MS. Academic Tutor. Expert Interview. 26 May 2020.

About This Article

Co-authored by:

Ronitte Libedinsky, MS

Academic Tutor

This article was co-authored by Ronitte Libedinsky, MS. Ronitte Libedinsky is an Academic Tutor and the Founder of Brighter Minds SF, a San Francisco, California based company that provides one-on-one and small group tutoring. Specializing in tutoring mathematics (pre-algebra, algebra I/II, geometry, pre-calculus, calculus) and science (chemistry, biology), Ronitte has over 10 years of experience tutoring to middle school, high school, and college students. She also tutors in SSAT, Terra Nova, HSPT, SAT, and ACT test prep. Ronitte holds a BS in Chemistry from the University of California, Berkeley, and an MS in Chemistry from Tel Aviv University. This article has been viewed 36,585 times.

18 votes - 78%

Co-authors: 16

Updated: February 7, 2023

Views: 36,585

Categories: Mathematics

Advertisement