Comment additionner des nombres impairs consécutifs

Coécrit par l'équipe de wikiHow

Bien sûr, il est toujours possible de calculer, à la main ou avec une calculatrice, la somme de tous les termes d'une suite de nombres impairs consécutifs commençant par 1, mais là où la tâche se complique, c'est lorsque la suite compte plusieurs dizaines de termes. Sachez qu'il existe une formule toute simple qui permet d'obtenir cette somme sans grands calculs. À l'opposé, il est aussi possible de résoudre le problème inverse, celui qui consiste à déterminer les nombres impairs consécutifs qu'il a fallu pour obtenir une somme donnée.

Partie 1
Partie 1 sur 3:

Additionner facilement des nombres impairs consécutifs

  1. Image intitulée Add a Sequence of Consecutive Odd Numbers Step 1
    1
    Partez du terme final de la suite. Avant toute chose, vous devez connaitre le terme final de la suite des nombres impairs consécutifs, c'est-à-dire le dernier terme de la suite. La formule qui vient permet de déterminer la somme de toute suite de ce type commençant par 1 [1] .
    • Si c'est un exercice que l'on vous a donné, on vous donnera ce terme final. Admettons qu'on vous demande de calculer la somme de tous les nombres impairs consécutifs entre 1 et 81, le terme final de la suite est donc 81.
  2. Image intitulée Add a Sequence of Consecutive Odd Numbers Step 2
    2
    Ajoutez 1 au terme final. C'est une addition simple qui permet d'obtenir un nombre pair, lequel va vous servir à l'étape suivante.
    • Ainsi, si votre terme final est 81, vous aurez : 81 + 1 = 82.
  3. Image intitulée Add a Sequence of Consecutive Odd Numbers Step 3
    3
    Divisez ce résultat par 2. Comme vous avez un nombre pair, vous pouvez donc le diviser par 2. Le résultat sera un nombre pair ou impair : peu importe, c'est le nombre total de termes de la suite.
    • Pour reprendre notre exemple, on a : 82 / 2 = 41.
  4. Image intitulée Add a Sequence of Consecutive Odd Numbers Step 4
    4
    Élevez ce résultat au carré. C'est la dernière étape qui consiste donc à multiplier ce résultat par lui-même, à l'élever donc au carré. Le résultat obtenu n'est rien d'autre que votre réponse finale.
    • Dans notre exemple, cela donne : 41 x 41 = 1 681. La somme de tous les nombres impairs consécutifs entre 1 et 81 est donc de 1 681.
    Publicité
Partie 2
Partie 2 sur 3:

Comprendre pourquoi une formule marche

  1. Image intitulée Add a Sequence of Consecutive Odd Numbers Step 5
    1
    Observez bien la structure de cette formule. Pour comprendre le pourquoi de cette formule, il faut la décomposer. La somme de tous les nombres impairs consécutifs d'une suite commençant par 1 est en fait égale au carré du nombre des termes qui ont été additionnés.
    • La somme (si on peut l'appeler ainsi !) du premier nombre impair est donc 1 (soit 1 x 1 = 12).
    • La somme de deux premiers nombres impairs est : 1 + 3 = 4 (soit 2 x 2 = 22).
    • La somme de trois premiers nombres impairs = 1 + 3 + 5 = 9 (soit 3 x 3 = 32).
    • La somme de quatre premiers nombres impairs = 1 + 3 + 5 + 7 = 16 (soit 4 x 4 = 42).
  2. Image intitulée Add a Sequence of Consecutive Odd Numbers Step 6
    2
    Comprenez bien ce qu'est cette valeur intermédiaire. Tout en résolvant ce problème de somme, vous apprenez aussi incidemment combien de termes ont été additionnés pour donner ce résultat, dans le cas présent 41 termes. Vous l'avez compris : dans une suite de nombres impairs consécutifs, le nombre de valeurs additionnées est égal à la racine carrée de la somme de ces dernières.
    • La somme du premier nombre impair est 1. La racine carrée de 1 est 1 : la suite ne comprend qu'un terme.
    • La somme de deux premiers nombres impairs est : 1 + 3 = 4. La racine carrée de 4 est 2 : la suite compte deux termes.
    • La somme des trois premiers nombres impairs est : 1 + 3 + 5 = 9. La racine carrée de 9 est 3 : la suite compte trois termes.
    • La somme de trois premiers nombres impairs est : 1 + 3 + 5 + 7 = 16. La racine carrée de 16 est 4 : la suite compte quatre termes.
  3. Image intitulée Add a Sequence of Consecutive Odd Numbers Step 7
    3
    Généralisez la formule. Si vous avez bien compris ce qui précède, vous êtes capable à présent d'écrire une formule pour une suite contenant n termes, c'est-à-dire n nombres impairs dont on cherche à calculer la somme. La formule de la somme des n nombres impairs consécutifs est donc : n x n (soit = n2 que l'on énonce « n au carré »).
    • Ainsi, si vous donnez à n la valeur 41, vous ferez : 41 x 41, soit 1 681, ce résultat étant la somme des 41 premiers nombres impairs.
    • Si vous ne savez pas combien de termes vous devez additionner, la formule de la somme entre 1 et n est la suivante : (1/2(n + 1))2. C'est la formule théorique.
    Publicité
Partie 3
Partie 3 sur 3:

Trouver des nombres impairs connaissant leur somme

  1. Image intitulée Add a Sequence of Consecutive Odd Numbers Step 8
    1
    Comprenez la différence entre les deux exercices. Si l'on vous donne une suite de nombres impairs consécutifs et qu'on vous demande d'en calculer la somme, vous devez utiliser la formule : (1/2(n + 1))2. Si à l'inverse, on vous donne la somme d'un certain nombre de nombres impairs et qu'on vous demande quels termes d'une suite ont été additionnés, vous devez utiliser une autre formule.
  2. Image intitulée Add a Sequence of Consecutive Odd Numbers Step 9
    2
    Posez que n est le premier nombre de la suite. Pour trouver quels nombres impairs consécutifs donnent telle somme, nous allons établir une formule générale, et c'est pourquoi nous partirons du premier terme de la suite que nous appellerons n [2] .
  3. Image intitulée Add a Sequence of Consecutive Odd Numbers Step 10
    3
    Exprimez les autres nombres en fonction de n. À présent, vous devez exprimer tous les nombres impairs suivants en fonction de n. Comme les nombres sont impairs et consécutifs, il y a par nature une différence de deux entre chaque nombre.
    • Cela signifie que le deuxième nombre de la suite commençant par n est n + 2, le troisième est n + 4, etc.
  4. Image intitulée Add a Sequence of Consecutive Odd Numbers Step 11
    4
    Établissez la formule. Pour cela, il faut qu'on vous donne le nombre de termes utilisés et, bien sûr, la somme de ces nombres. Vous mettrez à gauche du signe « = » la somme littérale des nombres, et à droite, la somme de ces nombres.
    • Admettons qu'on vous ait demandé quels sont les deux nombres impairs consécutifs ayant une somme égale à 128, vous écrirez l'égalité suivante : (n) + (n + 2) = 128.
  5. Image intitulée Add a Sequence of Consecutive Odd Numbers Step 12
    5
    Simplifiez l'équation. Pour tous les problèmes, vous additionnerez tous les n qui se trouvent dans le membre de gauche. C'est un passage obligé pour trouver vos nombres.
    • Ainsi, vous avez (n) + (n + 2) = 128, soit n + n + 2 = 128 qui peut se simplifier ainsi : 2n + 2 = 128.
  6. Image intitulée Add a Sequence of Consecutive Odd Numbers Step 13
    6
    Isolez n. La dernière étape consiste donc à trouver la valeur de n, c'est-à-dire à l'isoler d'un côté. Comme avec toute égalité, toute opération effectuée sur un membre doit l'être aussi sur l'autre.
    • Dans notre exemple très simple, pour faire disparaitre le 2 de gauche, vous devez soustraire 2 de chaque côté, ce qui donne l'égalité suivante : 2n + 2 - 2 = 128 - 2, soit 2n = 126.
    • Il ne reste plus qu'à trouver la valeur de n. Ici, c'est simple puisque vous devez diviser de chaque côté par 2, ce qui donne l'égalité suivante : 2n/2 = 126/2, soit n = 63
  7. Image intitulée Add a Sequence of Consecutive Odd Numbers Step 14
    7
    Inscrivez la réponse finale. À ce stade, vous savez que n = 63, mais vous n'en avez pas encore fini. Cette valeur n'est que la valeur de départ de votre suite. Or, on vous a demandé de trouver tous les termes de la suite qui donnent cette somme. Il faut donc calculer le ou les termes suivants
    • Dans notre exemple, les réponses sont 63 et 65, car vous avez donc n = 63, si bien que le terme suivant est : n + 2 = 65.
    • Bien entendu, il faut vérifier que les réponses sont bonnes. Faites l'addition des deux nombres consécutifs que vous avez trouvés pour vérifier que vous avez bien la somme donnée au départ. Si vous ne retombez pas sur cette somme, c'est que vous avez une erreur quelque part : refaites les calculs.
    Publicité

wikiHows en relation

calculer l'inverse d'une matrice 3x3
Comment
calculer l'inverse d'une matrice 3x3
calculer le diamètre d'un cercle
Comment
calculer le diamètre d'un cercle
calculer le rayon d’un cercle
Comment
calculer le rayon d’un cercle
calculer l'aire d'un quadrilatère
Comment
calculer l'aire d'un quadrilatère
calculer la diagonale d’un rectangle
Comment
calculer la diagonale d’un rectangle
calculer une note finale
Comment
calculer une note finale
calculer un écart type
Comment
calculer un écart type
calculer le déterminant d'une matrice 3 x 3
Comment
calculer le déterminant d'une matrice 3 x 3
calculer un intervalle de confiance
Comment
calculer un intervalle de confiance
calculer la valeur de résistances en série ou en dérivation
Comment
calculer la valeur de résistances en série ou en dérivation
calculer les probabilités de gagner à la loterie
Comment
calculer les probabilités de gagner à la loterie
calculer un pourcentage d'augmentation
Comment
calculer un pourcentage d'augmentation
calculer la longueur de l'hypoténuse
Comment
calculer la longueur de l'hypoténuse
calculer la hauteur d'un triangle
Comment
calculer la hauteur d'un triangle
Publicité

Références

  1. ↑ http://mathforum.org/k12/mathtips/addconsec.odd.html
  2. ↑ http://www.mathsteacher.com.au/year10/ch02_linear_equations/06_consecutive_numbers/cons.htm

À propos de ce wikiHow

l'équipe de wikiHow
Coécrit par:
l'équipe de wikiHow
Rédacteurs de wikiHow
Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.

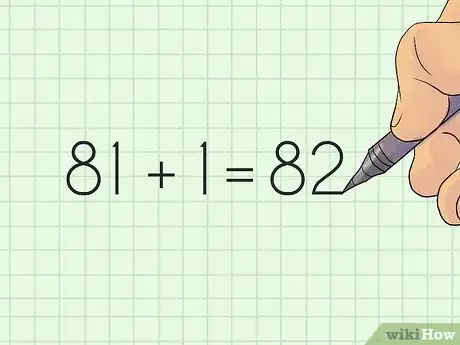
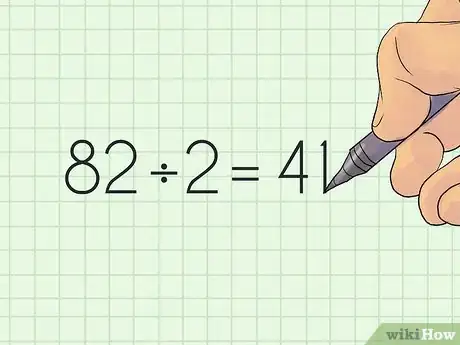
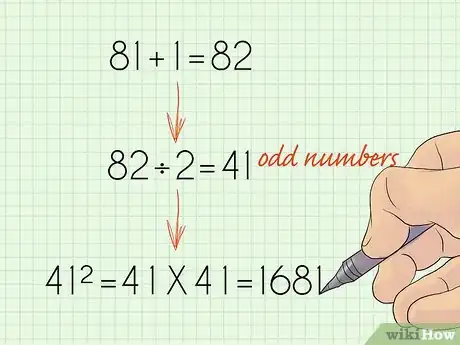
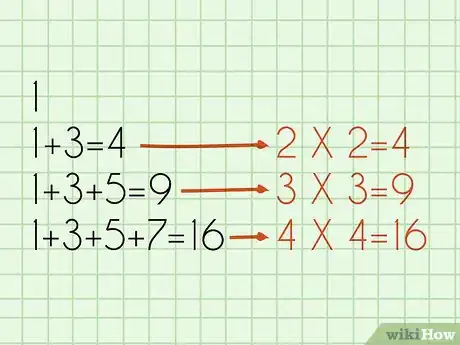
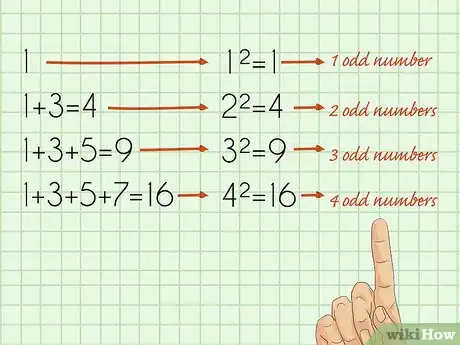
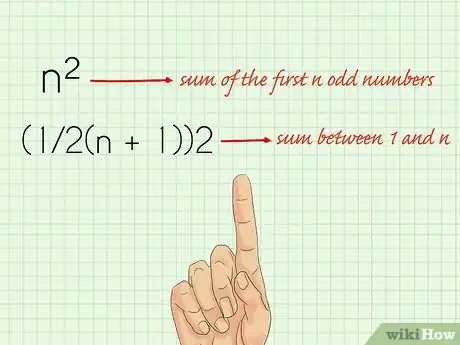
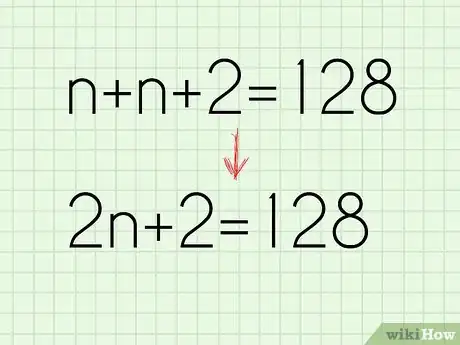
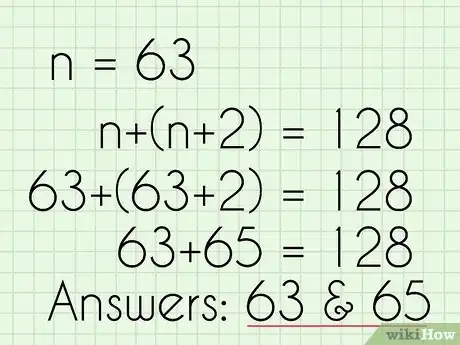
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 9 053 fois.
Catégories: Calculs
Publicité