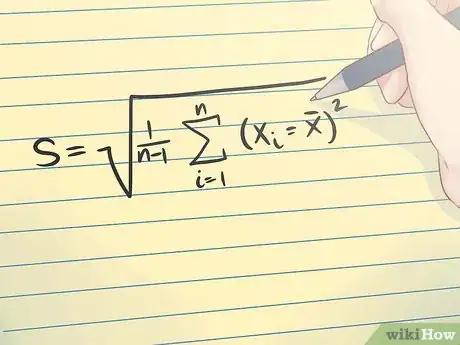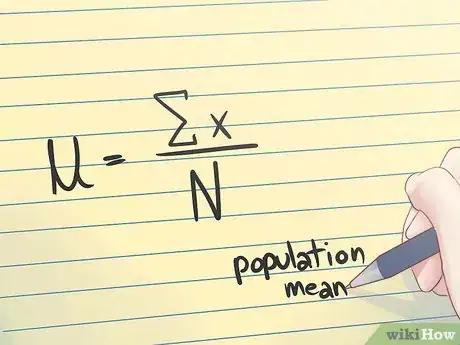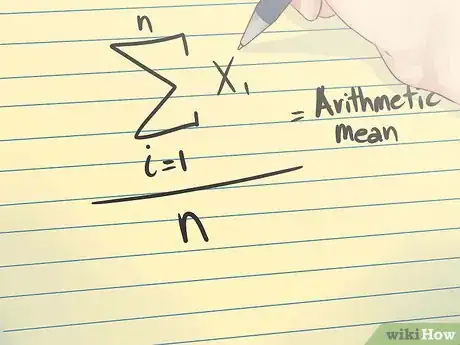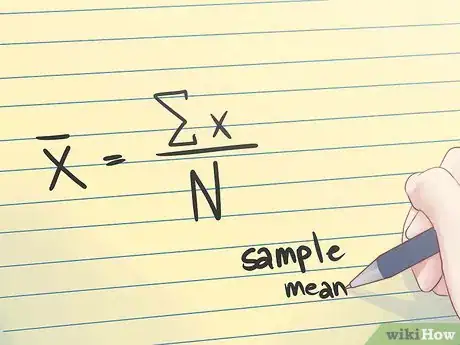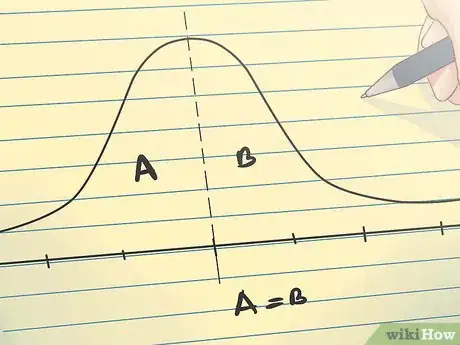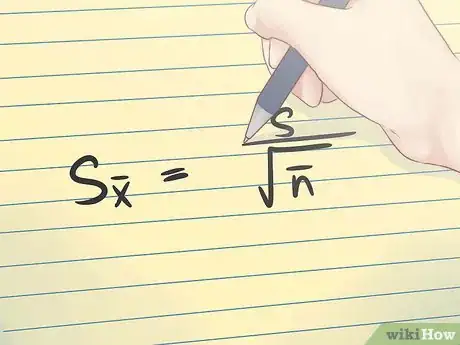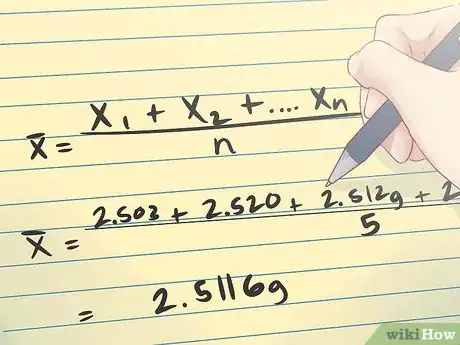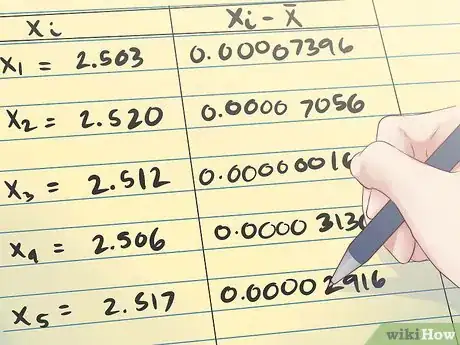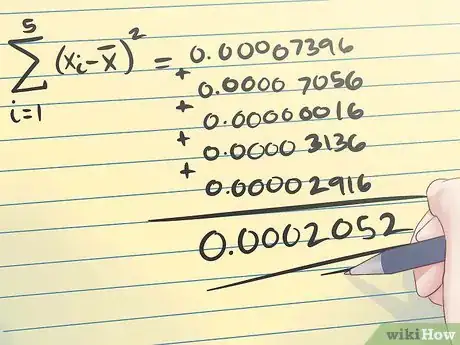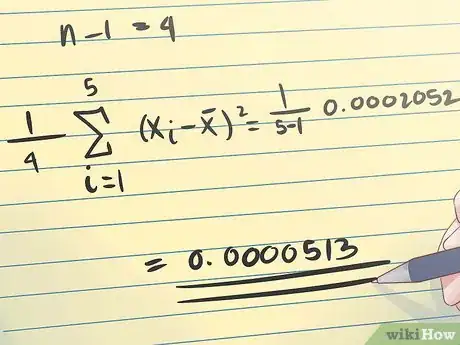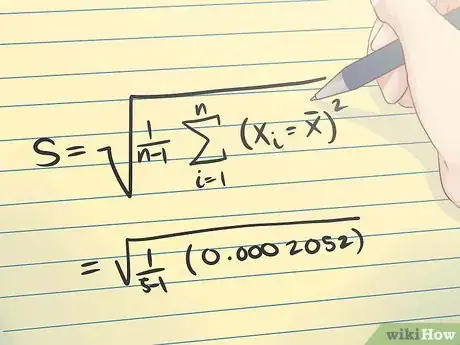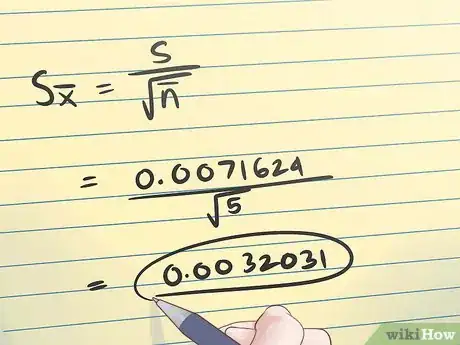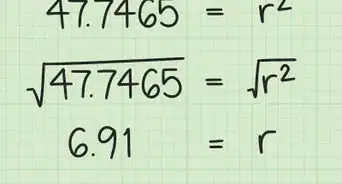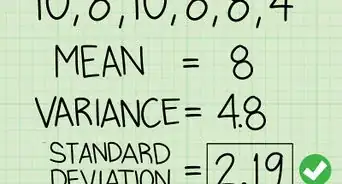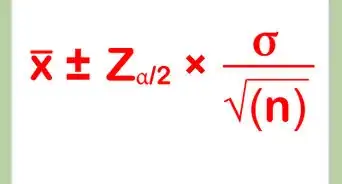Comment calculer l'erreur standard

Informations concernant l'auteur.e

L’« erreur standard » fait référence à la déviation standard de la distribution des valeurs d’un échantillon suivant une loi statistique. En d'autres termes, celle-ci peut être utilisée pour mesurer la précision de la moyenne d'un échantillon. Souvent, l'utilisation de l'erreur standard implique une distribution normale des valeurs de l’échantillon.

Partie 1

Partie 1 sur 3:

Comprendre les bases

1
Comprenez ce qu’est l’écart type. L’écart type d'un échantillon est une mesure de la dispersion des valeurs de cet échantillon. L’écart type d'un échantillon est généralement représenté par la lettre s. La formule mathématique de l’écart type est représentée sur l'image ci-dessus.
2
Comprenez ce qu'est la moyenne d'une population. La moyenne de la population constitue la moyenne des caractères quantitatifs ayant trait à la totalité de la population. En d'autres termes, il s'agit de la moyenne de toutes les valeurs et non pas d’un simple échantillon de ces valeurs.
3
Apprenez à calculer la moyenne arithmétique. La moyenne arithmétique n’est rien d’autre qu'une moyenne, c'est-à-dire la somme d’un ensemble de valeurs divisée par le nombre de valeurs de cet ensemble.
4
Sachez reconnaitre la moyenne d'un échantillon. Lorsqu’une moyenne arithmétique est basée sur une série d’observations obtenue à partir d’un échantillonnage dans une population statistique, on parle alors de « moyenne d'un échantillon ». Il s'agit de la moyenne d'un ensemble de valeurs qui inclut seulement une portion des individus d'un groupe. Vous trouverez la formule pour ce calcul dans l'image ci-dessus.
5
Comprenez ce qu’est une distribution normale. La distribution normale, qui est la distribution la plus fréquemment utilisée, est représentée par une courbe symétrique présentant un pic central au niveau de la moyenne des données. La forme de la courbe rappelle celle d'une cloche dont les bords retombent de façon symétrique de chaque côté de la moyenne. 50 % de la distribution des données se retrouve à gauche de la moyenne tandis que les 50 % restants se retrouvent à droite de celle-ci. La dispersion d'une distribution normale est déterminée par l’écart type.
6
Connaissez votre formule. La formule de l’erreur standard associée à la moyenne d’un échantillon est représentée sur l'image ci-dessus.

Publicité

Partie 2

Partie 2 sur 3:

Calculer l’écart type

1
Calculez la moyenne de l'échantillon. Pour trouver l’erreur standard, vous devez dans un premier temps déterminer la valeur de l’écart type s (car celui-ci entre dans la composition de la formule de l’erreur standard). Commencez par calculer la moyenne des valeurs de votre échantillon. La moyenne de votre échantillon est la moyenne arithmétique des mesures x1, x2... xn. La formule de cette moyenne est représentée sur l' image ci-dessus.
- Par exemple, imaginons que vous deviez calculer l'erreur standard associée à la moyenne des masses de cinq pièces, listées dans le tableau ci-dessous.
  Pour calculer la moyenne de l'échantillon, vous devez introduire les valeurs des masses dans la formule de la façon suivante.
2
Soustrayez la moyenne de l'échantillon de chaque mesure et élevez la valeur obtenue au carré. Une fois que vous aurez calculé la moyenne de l'échantillon, vous pourrez la soustraire de chaque mesure individuelle avant d'élever le résultat au carré.
- Suivant l'exemple ci-dessus, votre tableau ressemblerait à quelque chose comme ça.
3
Trouvez la déviation totale des mesures par rapport à la moyenne de l'échantillon. La déviation totale est égale à la moyenne des écarts à la moyenne de l'échantillon élevés au carré. Pour ce faire, additionnez l'ensemble de ces nouvelles valeurs.
- Toujours en suivant l'exemple ci-dessus, votre calcul devrait être le suivant.
  Cette équation vous donne la déviation quadratique totale des mesures par rapport à la moyenne de l'échantillon. Vous remarquerez que le signe de ces différences n'a pas d’importance.
4
Calculez la déviation quadratique moyenne de vos mesures par rapport à la moyenne de l'échantillon. Une fois que vous aurez calculé la déviation totale, Vous pourrez obtenir la déviation moyenne en divisant votre résultat par n -1. Remarquez que n est égal au nombre de mesures de votre échantillon.
- Dans l'exemple ci-dessus, votre échantillon comprend cinq mesures. n -1 est donc égal à 4. Voici comment faire ce calcul.
5
Trouvez la déviation standard. Vous possédez à présent toutes les valeurs nécessaires pour appliquer la formule de l'écart type s.
- Suivant l'exemple ci-dessus, voici comment calculer l'écart type.
  La valeur de votre écart type est donc de 0,007.
Publicité

Partie 3

Partie 3 sur 3:

Calculer l’erreur standard

1
Utilisez la valeur de l’écart type pour calculer celle de l’erreur standard, en utilisant la formule classique.
- Suivant l’exemple précédent, voici comment calculer l’erreur standard.
  La valeur de votre erreur standard (soit l’erreur standard associée à la moyenne de votre échantillon) est donc de 0,003 gramme.

Conseils

On confond souvent erreur standard et écart type. L’erreur standard est une description de la déviation standard de la distribution d’une loi statistique, et non pas de la distribution de valeurs individuelles.
Dans les journaux spécialisés, on ne fait souvent pas la distinction entre erreur standard et écart type. Le signe ± est utilisé dans les deux cas.