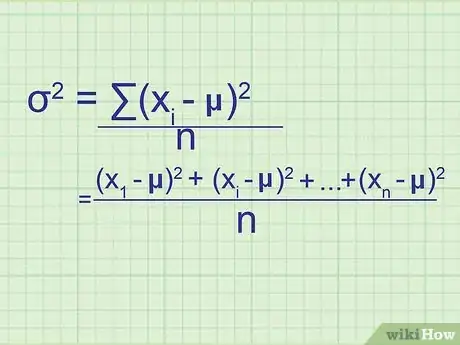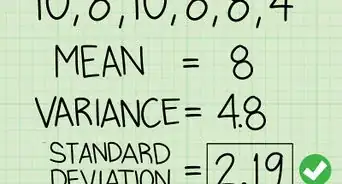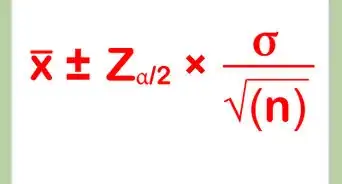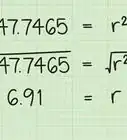Comment calculer la variance

La variance est une mesure de la dispersion d'une série de données. Une variance faible indique que les nombres de la série de données sont proches l'un de l'autre. Une variance élevée indique que les nombres sont très distants. Ce concept est très utilisé en statistiques. Par exemple, la comparaison de la variance entre deux séries de données (tels que les résultats d'un patient mâle et femelle) est une manière de vérifier si une variable a un effet remarquable ^{[1]
X
Source de recherche}. La variance est aussi utile dans la création des modèles statistiques, car une variance faible peut être un signe de surparamétrage ^{[2]
X
Source de recherche}.

Méthode 1

Méthode 1 sur 2:

Calculer la variance d'un exemple

1
Écrivez votre échantillon de série de nombres. Dans la plupart des cas, les statisticiens ont uniquement accès à un échantillon ou une sous-série de la population qu'ils étudient. Par exemple, au lieu d'analyser le cout de chaque voiture de la population en Allemagne, un statisticien pourrait trouver le cout d'un échantillon aléatoire de quelques milliers de voitures. Il peut utiliser cet échantillon pour obtenir une bonne estimation des couts des voitures allemandes, mais cela pourrait ne pas correspondre exactement aux couts réels.
- Exemple : l'analyse des nombres de muffins vendus chaque jour dans une cafétéria vous a permis d'obtenir cet échantillon aléatoire sur 6 jours : 17, 15, 23, 7, 9, 13. Cette série de nombres est un échantillon et non une population, puisque vous ne disposez pas des nombres de muffins vendus par jour depuis l'ouverture de la cafétéria.
- Si vous disposez de toutes les données journalières depuis la création de la cafétéria, vous pouvez calculer la variance de la population comme décrite dans la deuxième méthode de cet article.
2
Notez la formule de la variance de l'échantillon. La variance d'une série de données indique à quel point les données sont distantes. Plus la variance est proche de zéro, plus les données sont proches l'une de l'autre. Lorsque vous travaillez avec des échantillons de séries de données, utilisez la formule suivante pour calculer la variance ^{[3]
X
Source de recherche}.
- $s^{2}$ = ^{∑[( $x_{i}$ - x̅) $^{2}$ ]}/_{(n - 1)}
- $s^{2}$ est la variance. La variance est toujours mesurée en unité carrée.
- $x_{i}$ représente un terme de votre série de données.
- Le signe ∑, signifiant la somme indique de calculer les termes suivants pour chaque valeur de $x_{i}$ , puis de les additionner.
- x̅ est la moyenne de l'échantillon.
- n est le nombre de données de la série.
3
Calculez la moyenne d'un échantillon. Le symbole x̅ ou x-barre se réfère à la moyenne d'un échantillon ^{[4]
X
Source de recherche}. Calculez cela comme toute autre moyenne : sommez toutes les données puis divisez le résultat par le nombre de données existantes.
- Exemple : d'abord, sommez toutes les valeurs des données : 17 + 15 + 23 + 7 + 9 + 13 = 84.
  Ensuite, divisez le résultat par le nombre de données dans la série, qui est dans ce cas : 84 ÷ 6 = 14.
  Moyenne de l'échantillon = x̅ = 14.
- Vous pouvez considérer la moyenne comme le milieu ou centre de la série. Si les données sont proches de la moyenne, la variance est faible. Si c'est le contraire, alors la variance sera élevée.
4
Soustrayez la moyenne de chaque valeur de donnée. Maintenant, vous devez calculer $x_{i}$ $x_{i}$ - x̅, où $x_{i}$ $x_{i}$ représente chaque nombre de votre série de données. Chaque résultat indique la distance de ce nombre à la moyenne ou en d'autres mots, permet de savoir à quel point la valeur est distante de la moyenne ^{[5]
X
Source de recherche}.
- Exemple :
  $x_{1}$ - x̅ = 17 - 14 = 3
  $x_{2}$ - x̅ = 15 - 14 = 1
  $x_{3}$ - x̅ = 23 - 14 = 9
  $x_{4}$ - x̅ = 7 - 14 = -7
  $x_{5}$ - x̅ = 9 - 14 = -5
  $x_{6}$ - x̅ = 13 - 14 = -1
- Vous pouvez vérifier vos calculs, sachant que la somme des résultats devrait donner zéro. Cela est possible, car les réponses négatives (la distance entre la moyenne et les petites valeurs) annulent exactement les réponses positives (distance entre la moyenne et les plus grandes valeurs).
5
Élevez au carré chaque résultat. Comme dit ci-dessus, la somme des déviations ( $x_{i}$ $x_{i}$ - x̅) donne zéro. Cela signifie que la déviation moyenne sera toujours égale à 0, donc cela ne nous informe pas du niveau de dispersion de la série. Pour résoudre ce problème, élevez au carré chaque déviation. Ainsi, tous les nombres seront positifs et leur somme ne donnera plus zéro.
- Exemple :
  ( $x_{1}$ - x̅) $^{2}=3^{2}=9$
  $(x_{2}$ - x̅) $^{2}=1^{2}=1$
  9² = 81
  (-7)² = 49
  (-5)² = 25
  (-1)² = 1
- Vous avez maintenant la valeur ( $x_{i}$ - x̅) $^{2}$ pour chaque donnée de votre échantillon.
6
Sommez les valeurs au carré. Il est temps de calculer le numérateur de la formule : ∑[( $x_{i}$ $x_{i}$ - x̅) $^{2}$ $^{2}$ ]. Le signe ∑ indique la somme des valeurs suivant le signe pour chaque valeur de $x_{i}$ $x_{i}$ . Vous avez déjà calculé ( $x_{i}$ $x_{i}$ - x̅) $^{2}$ $^{2}$ pour chaque valeur de $x_{i}$ $x_{i}$ dans votre échantillon, donc tout ce que vous avez à faire c'est sommer tous les résultats.
- Exemple : 9 + 1 + 81 + 49 + 25 + 1 = 166.
7
Divisez par n - 1, où n est le nombre de données. Auparavant, les statisticiens divisaient seulement par n lors du calcul de la variance d'un échantillon. Cela donne la valeur moyenne de la déviation au carré, ce qui correspond parfaitement à la variance de notre échantillon. Mais souvenez-vous que l'échantillon est juste une estimation d'une grande population. Si vous prenez un autre échantillon aléatoire et faites les mêmes calculs, vous obtiendrez un résultat différent. Pour cela, diviser par n - 1 au lieu de n vous donnera une meilleure estimation de la variance de la plus grande population, qui est l'aspect qui nous intéresse vraiment. Cette correction est si commune qu'elle est maintenant acceptée pour la définition et le calcul de la variance d'un échantillon ^{[6]
X
Source de recherche}.
- Exemple : il y a six données dans notre échantillon, alors n = 6.
  La variance de l'échantillon = $s^{2}={\frac {166}{6-1}}=$ 33,2.
8
Comprenez la variance et l'écart-type. Notez que puisqu'il y a un exposant dans la formule, la variance est mesurée en unité carrée des données originales. Cela peut être difficile à comprendre intuitivement. Au lieu de cela, c'est souvent plus pratique d'utiliser l'écart-type qui est encore la racine carrée de la variance. C'est pourquoi la variance d'un échantillon se note $s^{2}$ $s^{2}$ et l'écart-type $s$ $s$ .
- Par exemple, l'écart-type de l'échantillon ci-dessus est s = √33,2 = 5,76.
Publicité

Méthode 2

Méthode 2 sur 2:

Calculer la variance d'une population

1
Commencez avec la série de données d'une population. Le terme population se réfère à la série totale des observations relevantes. Par exemple, si vous étudiez l'âge des résidents du Texas, votre population doit inclure l'âge de chaque résident du Texas. Vous devriez normalement créer un tableau pour une série de données si grande, mais voici un exemple d'une petite série de données.
- Exemple : il y a exactement 6 tanks de poissons dans une chambre d'aquarium. Les six tanks contiennent les nombres de poissons suivants :
  $x_{1}=5$
  $x_{2}=5$
  $x_{3}=8$
  $x_{4}=12$
  $x_{5}=15$
  $x_{6}=18$
2
Notez la formule de la variance de la population. Puisque la population comporte toutes les données dont vous avez besoin, cette formule vous donnera la variance exacte de la population. Pour distinguer cette formule de celle de la variance d'un échantillon (qui n'est qu'une estimation), les statisticiens utilisent différentes variables ^{[7]
X
Source de recherche}.
- σ $^{2}$ = ^{(∑( $x_{i}$ - μ) $^{2}$ )}/_n.
- Variance de la population = σ $^{2}$ . C'est un sigma minuscule au carré. La variance est mesurée en unité carrée.
- $x_{i}$ représente un terme dans votre série de données.
- Les termes après le ∑ seront calculés pour chaque valeur de $x_{i}$ , puis sommés.
- μ est la moyenne de la population.
- n est le nombre de données dans la population.
3
Trouvez la moyenne de la population. Lorsque vous analysez une population, le symbole μ représente la moyenne arithmétique. Pour trouver la moyenne, additionnez toutes les données, puis divisez le résultat par le nombre de données.
- Considérons l'exemple ci-dessous.
- Exemple : moyenne = μ = ${\frac {5+5+8+12+15+18}{6}}$ = 10,5.
4
Soustrayez la moyenne de chaque donnée. Pour les données proches de la moyenne, le résultat sera proche de zéro. Répétez le problème de soustraction pour chaque donnée et vous commencerez à avoir une notion de la dispersion des données.
- Exemple :
  $x_{1}$ - μ = 5 - 10,5 = -5,5
  $x_{2}$ - μ = 5 - 10,5 = -5,5
  $x_{3}$ - μ = 8 - 10,5 = -2,5
  $x_{4}$ - μ = 12 - 10,5 = 1,5
  $x_{5}$ - μ = 15 - 10,5 = 4,5
  $x_{6}$ - μ = 18 - 10,5 = 7,5.
5
Élevez chaque réponse au carré. Maintenant certaines de vos valeurs de l'étape précédente seront négatives et d'autres seront positives. Si vous faites une représentation de vos données sur une ligne de nombres, les réponses négatives représentent les nombres à gauche de la moyenne et les réponses positives les nombres à droite de la moyenne. Cela n'est pas bon pour le calcul de la variance, car la somme de ces nombres donnera zéro. Pour éviter cela, élevez chaque réponse au carré.
- Exemple :
  ( $x_{i}$ - μ) $^{2}$ pour chaque valeur de i de1 à 6 :
  (-5,5) $^{2}$ = 30,25
  (-5,5) $^{2}$ = 30,25
  (-2,5) $^{2}$ = 6,25
  (1,5) $^{2}$ = 2,25
  (4,5) $^{2}$ = 20,25
  (7,5) $^{2}$ = 56,25.
6
Trouvez la moyenne de vos réponses. Maintenant, vous avez une valeur pour chaque donnée liée (indirectement) à la distance de cette donnée par rapport à la moyenne. Calculez la valeur de ces résultats en les sommant puis en les divisant par le nombre de valeurs.
- Exemple :
  variance de la population = ${\frac {30,25+30,25+6,25+2,25+20,25+56,25}{6}}={\frac {145,5}{6}}=$ 24,25.
7
Reliez cela à la formule. Si vous ne savez pas comment relier cela à la formule fournie au début de cette méthode, essayez d'écrire le problème d'une façon détaillée.
- Après avoir calculé la différence entre la moyenne et la valeur au carré, vous avez les valeurs ( $x_{1}$ - μ) $^{2}$ , ( $x_{2}$ - μ) $^{2}$ et ainsi de suite jusqu'à ( $x_{n}$ - μ) $^{2}$ , où $x_{n}$ est la dernière donnée dans la série.
- Pour trouver la moyenne de ces valeurs, il suffit de les additionner puis les diviser par n : ( ( $x_{1}$ - μ) $^{2}$ + ( $x_{2}$ - μ) $^{2}$ + ... + ( $x_{n}$ - μ) $^{2}$ ) / n
- Après avoir récrit le numérateur sous la notation du sigma, vous aurez ^{(∑( $x_{i}$ - μ) $^{2}$ )}/_n, qui est la formule de la variance.
Publicité

Conseils

Puisqu'il est difficile d'interpréter la variance, cette valeur est généralement calculée comme point de départ pour le calcul de l'écart-type.
L'utilisation de n-1 au lieu de n dans le dénominateur lors de l'analyse des échantillons est une technique appelée fonction de Bessel. L'échantillon n'est qu'une estimation de la population entière et la moyenne de l'échantillon est biaisée pour correspondre à cette estimation. Cette correction de Bessel supprime ce biais.^{[8]
X
Source de recherche}. Cela s'explique par le fait qu'une fois que vous avez énuméré n - 1 données, le dernier n est déjà limité, puisque seules certaines valeurs sont prises en compte dans le calcul de la moyenne de l'échantillon (x̅) utilisé dans la formule de la variance ^{[9]
X
Source de recherche}.