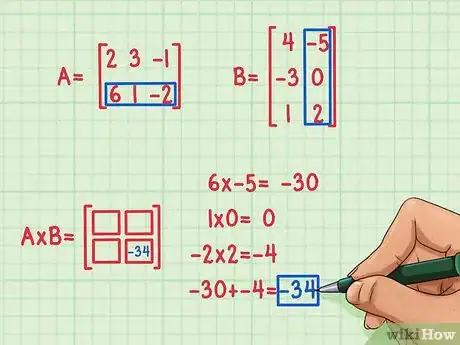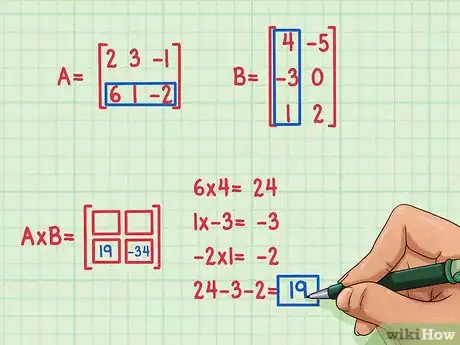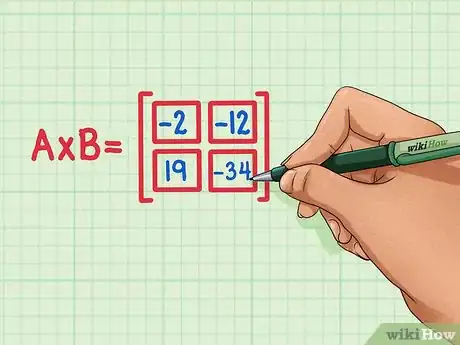wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, 12 personnes, certaines anonymes, ont participé à son édition et à son amélioration au fil du temps.
Cet article a été consulté 33 505 fois.
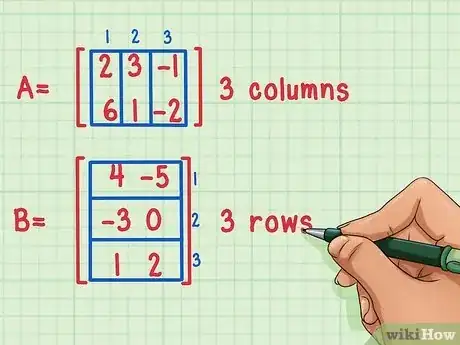
Une matrice est une disposition rectangulaire de nombres, de symboles ou d'expressions dans des rangées et des colonnes. Pour multiplier des matrices, vous devez multiplier les éléments (ou les nombres) de la rangée de la première matrice par les éléments des rangées de la seconde matrice puis additionner leurs produits. Vous pouvez multiplier les matrices en quelques étapes simples qui comprennent l'addition, la multiplication et un bon positionnement des résultats.
Étapes
-
1Vérifiez si les matrices peuvent être multipliées. La multiplication des matrices ne peut se faire que si le nombre de colonnes de la première matrice est égal au nombre de rangées de la seconde matrice.
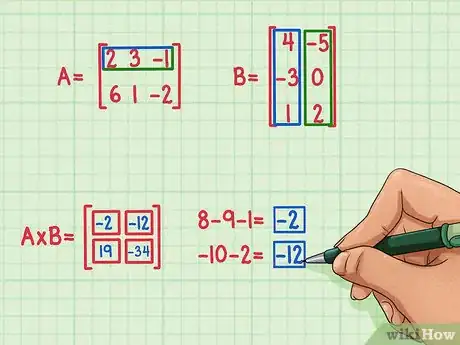
- Ces matrices peuvent être multipliées parce que la première matrice Matrice A a 3 colonnes et la seconde matrice Matrice B a 3 rangées.
-
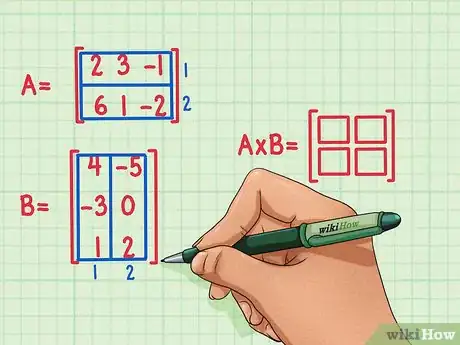
2Marquez les dimensions du produit de la matrice. Créez une nouvelle matrice vide qui marquera les dimensions du produit de la matrice, le produit des deux matrices. La matrice qui représente le produit de la matrice A et de la matrice B aura le même nombre de rangées que la première matrice et le même nombre de colonnes que la seconde matrice. Vous pouvez dessiner des cases vides pour indiquer le nombre de colonnes et de rangées de cette matrice.
- La matrice A a 2 rangées, alors le produit de la matrice aura 2 rangées.
- La matrice B a 2 colonnes, alors le produit de la matrice aura 2 colonnes.
- Le produit de la matrice aura 2 rangées et 2 colonnes.
-
3Trouvez le premier produit scalaire. Pour trouver un produit scalaire, vous devez multiplier le premier élément dans la première rangée par le second élément de la première colonne et le troisième élément de la première rangée par le troisième élément de la première colonne. Puis additionnez leurs produits pour trouver le produit scalaire. Considérons que vous avez décidé de résoudre premièrement l'élément de la 2ème rangée et de la 2ème colonne (en bas à droite) du produit de la matrice. Voici comment faire :
- 6 × -5 = -30
- 1 × 0 = 0
- -2 × 2 = -4
- -30 + 0 + (-4) = -34
- Le produit scalaire est -34 et restera en bas à droite du produit de la matrice.
- Lorsque vous multipliez les matrices, le produit scalaire doit être dans la rangée de la première matrice et dans la colonne de la seconde matrice. Par exemple, si vous trouvez le produit scalaire de la rangée inférieure de la matrice A et de la colonne de droite de la matrice B, la réponse -34, sera dans la rangée inférieure et dans la colonne de droite du produit de la matrice.
-
4Trouvez le second produit scalaire. Considérons que vous voulez trouver le terme en bas à gauche du produit de la matrice. Pour trouver ce terme, il suffit de multiplier les éléments de la rangée inférieure de la première matrice par les éléments de la première colonne de la seconde matrice puis les additionner. Utilisez la même méthode que vous avez utilisée pour multiplier la première rangée et colonne -- trouvez à nouveau le produit scalaire.
- 6 × 4 = 24
- 1 × (-3) = -3
- (-2) × 1 = -2
- 24 + (-3) + (-2) = 19
- Le produit scalaire est -19 et restera en bas à gauche du produit de la matrice.
-
5Trouvez les deux produits scalaires restants. Pour trouver le terme en haut à gauche du produit de la matrice, commencez par le produit scalaire de la rangée supérieure de la matrice A et la colonne de gauche de la matrice B. Voici comment faire :
- 2 × 4 = 8
- 3 × (-3) = -9
- (-1) × 1 = -1
- 8 + (-9) + (-1) = -2
- Le produit scalaire est -2 et restera en bas à gauche du produit de la matrice.
- Pour trouver le terme en haut à droite du produit de la matrice, il suffit de trouver le produit scalaire de la rangée supérieure de la matrice A et de la colonne de droite de la matrice B. Voici comment faire :
- 2 × (-5) = -10
- 3 × 0 = 0
- (-1) × 2 = -2
- -10 + 0 + (-2) = -12
- Le produit scalaire est -12 et restera en haut à droite du produit de la matrice.
-
6Vérifiez si tous les quatre produits scalaires sont à leurs emplacements corrects dans le produit de la matrice. 19 serait en bas à gauche, -34 serait en bas à droite, -2 serait en haut à gauche et -12 serait en haut à droite.Publicité
Conseils
- Le produit de deux matrices doit avoir le même nombre de rangées que la première matrice et le même nombre de colonnes que la seconde matrice.
- Utiliser des segments au lieu des droites peut vous donner des réponses fausses. Si la droite représentant une rangée a besoin d'être prolongée pour croiser une colonne, alors prolongez-la ! Ceci n'est qu'une technique de visualisation pour pouvoir facilement déterminer laquelle des rangées et des colonnes doit être utilisée pour résoudre chaque élément du produit.
- Notez vos calculs. La multiplication des matrices inclut beaucoup de calculs, vous pouvez être distrait et vous embrouiller avec les nombres.