أوكتونيون
أوكتونيون Octonion في الرياضيات هي امتداد كعملية غير تجميعية للكواتيرنيون.[1][2][3] أبعادها الثمانية الحقيقية الجبرية في حقل الأعداد الحقيقية هو أوسع حقل بعدي من الممكن الحصول عليه باستخدام إنشاء كايلي-ديكسون. يرمز جبرياً إلى الأوكتونيون بالرمز O أو بالحرف العريض .
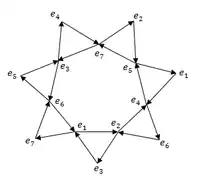
ربما بسبب أن الأوكتونيون لاتحقق الخاصة التجميعية لعملية الضرب، فإنها تجذب اهتماماً أقل من الكواتيرنيون، ولكن وعلى الرغم من شهرتها الضئيلة هذه فإن الأوكتونيون لها تطبيقات عدة في مجالات نظرية الأوتار، النسبية الخاصة، المنطق الكوانتي.
التاريخ
تم اكتشاف الأوكتونيون في عام 1843 من قبل العالم جون ت. غرافس، صديق ويليام هاملتون مكتشف الكواتيرنيون.
التعريف
من الممكن اعتبار الأوكتونيون على أنها مجموعات ثمانية (مثل الألحان الثمانية المعد لثماني آلات موسيقية أو مغنينن) من الأعداد الحقيقية. كل أوكتونيون هي اندماج خطي حقيقي لوحدات الزمرة الثمانية البسيطة {1, i, j, k, l, il, jl, kl}، وعليه فإن أي أوكتونيون x يكون ممكن الكتابة على الشكل التالي:
ذات مكافئ حقيقي xa.
عملية جمع الأوكتونيون تتم بجمع المكافئات المتوافقة، تماماً مثل الأعداد العقدية وكواتيرنيون. عملية الضرب في الأوكتونيون محددة بشكل كامل بجدول الضرب التالي:
| 1 | i | j | k | l | il | jl | kl |
|---|---|---|---|---|---|---|---|
| i | −1 | k | −j | il | −l | −kl | jl |
| j | −k | −1 | i | jl | kl | −l | −il |
| k | j | −i | −1 | kl | −jl | il | −l |
| l | −il | −jl | −kl | −1 | i | j | k |
| il | l | −kl | jl | −i | −1 | −k | j |
| jl | kl | l | −il | −j | k | −1 | −i |
| kl | −jl | il | l | −k | −j | i | −1 |
إنشاء كايلي-ديكسون
هناك طريقة أكثر منطقية في تعريف الأوكتونيون باستخدام إنشاء كايلي-ديكسون. حيث كما أنه من الممكن تعريف الكواتيرنيون على أنها زوج من الأعداد العقدية، يمكن تعريف الأوكتونيون على أنها زوج من الكواتيرنيون. حيث يعطى جداء زوجين من الكواتيرنيون (a, b) و(c, d) على النحو التالي:
حيث هو نظير الكواتيرنيون z.
النظير، الطويلة، المقلوب
يعطى نظير الأوكتونيون التالية
بالعلاقة:
يعرف الجزء الحقيقي للأوكتونيون x بالعلاقة:
½x + x*) = x0)
كما يعرف الجزء التخيلي بالعلاقة:
½(x - x*)
تعطى طويلة الأوكتونيون x بالعلاقة:
يعطى الجذر التربيعي هنا بالعلاقة: وهو دائماً عدد حقيقي غير سالب:
وهذه الطويلة تتوافق مع الطويلة في الفضاء الإقليدي من البعد الثامن R8.
إن وجود طويلة للأوكتونيون يتطلب وجود مقلوب لكل أوكتونيون غير صفري. حيث يعطى مقلوب x ≠ 0 بالعلاقة:
وهي تحقق
.
مراجع
- (Baez 2002, p. 6)
- Hamilton (1848)، "Note, by Sir W. R. Hamilton, respecting the researches of John T. Graves, Esq."، Transactions of the Royal Irish Academy، 21: 338–341، مؤرشف من الأصل في 26 أبريل 2018
- G Gentili, C Stoppato, DC Struppa and F Vlacci (2009)، "Recent developments for regular functions of a hypercomplex variable"، في Irene Sabadini؛ M Shapiro؛ F Sommen (المحررون)، Hypercomplex analysis (ط. Conference on quaternionic and Clifford analysis; proceedings)، Birkhäuser، ص. 168، ISBN 978-3-7643-9892-7، مؤرشف من الأصل في 4 ديسمبر 2016
{{استشهاد}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)
- بوابة رياضيات