عدد طبيعي

يُعتقد أن عظمة إشانغو (معروضة في المعهد الملكي البلجيكي للعلوم الطبيعية)[2][3] كانت مستخدمة في الحسابات منذ 20000 سنة.

في البدايات مُثِلَت الأرقام الطبيعية عن طريق وضع علامة للشيء المعدود. منها تطور لمقارنة الأشياء المعدودة بأخرى لمعرفة الزيادة والنقصان أو المساواة - عن طريق حذف شيء وشطب علامته أو إضافة آخر مع علامة له وهكذا.[4][5]

شكل نظام العد خطوة هامة في تطور تمثيل الأرقام، لأنه مَكَّنَ الإنسان من تسجيل أعداد كبيرة.

فالمصريون القدماء كان لديهم نظام عد استخدم رموزا هيروغليفية مختلفة لتمثيل 1 و10 وجميع القوى من 10 لأكثر من 1مليون. فهناك نقش حجري في الكرنك يعود تاريخه إلى حوالي 1500قبل الميلاد (الآن في متحف اللوفر)، مثل فيه الرقم 276 كـ 2 من فئة المئات، و7 من فئة العشرات و 6 من فئة الآحاد. وبنفس الطريقة للرقم 4622.

والبابليون كان لديهم نظام عد قيمة الموضع اعتمد على الأرقام من 1 إلى 10، مستخدما قاعدة ستينية، وفيه رمز العدد 60 هو نفس رمز العدد 1 ويميز بينهم السياق.[6]

لاحقا تطور نظام العد ليشمل تخصيص رمز للصفر باعتباره رقم. استخدام رقم للصفر في نظام القيمة الموضعية يعود للبابليين حوالي 700 ق. م.، حيث حذفوا هذا الرقم لو كان آخر رقم في العدد.[arabic-abajed 2]

استخدمت حضارات الأولمك والمايا الصفر كرقم حوالي بدايات القرن 1 ق م، لكنه لم ينتشر خارج أمريكا الوسطى.[8][9]

في العصر الحديث بدأ استخدام الصفر مع عالم الرياضيات الهندي براهماجوبتا حوالي 628 م. ولكن مع ذلك، استخدم ديونيسيوس الصغير في 525 م الصفر كرقم لحساب عيد الفصح، دون أن يُشار له كرقم (حيث لا تتضمن الأرقام الرومانية القياسية رمز الصفر). واستخدمت مكانه كلمة nulla (أو صيغة المضاف nullae) من nullus ، وتعني باللاتينية «لا شيء»، للإشارة لقيمة الصفر.[10]

أول دراسة منهجية للأرقام كمفهوم مجرد تُنسب عادة للفلاسفة اليونانيين فيثاغورس وأرخميدس. اعتبر بعض علماء الرياضيات اليونانيون أن الرقم 1 يختلف عن الأعداد الأكبر منه، وأحيانًا لا يعتبر كعدد.[arabic-abajed 3] ، مثلًا عرّف إقليدس أولًا الوحدة

الوحدة شيء به يمتنع الموجود عن الانقسام إلى اشيآء تشاركه في تمام ذاتياته[12]

، وبالتالي وفقًا لتعريفه، فإن الوحدة (الرقم 1) ليست عددًا[arabic-abajed 4]، ويعرف العدد على أنه الكمية المؤلفة من الوحدات.[13]

كما دُرِسَتْ الأرقام تقريبًا في نفس الوقت في الهند والصين وأمريكا الوسطى.[14]

في القرن التاسع عشر في أوروبا، كان هناك نقاش رياضي وفلسفي حول ماهية الأعداد الطبيعية. على سبيل المثال هنري بوانكاريه ممثلا للفلسفة الطبيعانية نَقَدَ تعريف الرياضيون (كـ فريجه، وديدكايند، وراسل) الأرقام منطقيًا لأنه سيؤدي لتناقضات والوقوع في فخ التعريفات الدائرية، بدلا من ذلك اعتبر أن الأرقام هي نتاج طبيعي للنفس البشرية وطبيعة الأشياء من حولنا[15]، وهي تتوافق مع رؤية كرونيكر، الذي قال «خَلَقَ الله الأعداد الصحيحة، غير ذلك من صنيع البشر».[arabic-abajed 5]

بسبب انتقادات الطبيعانيين، رأي البنائيون (constructivists) الحاجة لتطوير أساس الرياضيات المنطقي ليصبح أكثر دقة.[arabic-abajed 6]

في ستينيات القرن التاسع عشر، اقترح جراسمان لأول مرة وباستخدام الاستقراء الرياضي تعريفًا ذاتيًا للأعداد الطبيعية، بدءًا بالصفر ثم مضيفا له واحد (قيمة سماها e) للحصول على الرقم التالي[18]، هو ما يعني بالتبعية أنها نتاج لاستخدام دالة الاستقراء f(n+1) المعرفة بدورها من الدالة الأولى f(0) وليست نتاج طبيعي بشكل تام.

بدأ فريجه تعريف الأرقام مستخدما نظرية المجموعات. في البداية عرَّفَ الرقم الطبيعي على أنه فئة جميع المجموعات التي تكون في تقابل واحد لواحد مع مجموعة معينة. ولكن أدى هذا التعريف لمفارقات، كمفارقة راسل. لتجنب ذلك، عُدِّلَ التعريف لينص على أن الرقم الطبيعي هو مجموعة بعينها، وأن أي مجموعة في تقابل واحد لواحد معها تحوي هذا العدد من العناصر.[19]

من بعد فريجه، قدم بيرس تعريفًا، وحَسَّنَهُ ديديكيند، وطوره بيانو بصورة أكبر فيما يعرف الآن بمسلمات بيانو. وهو يعتمد على مسلمات خصائص الأعداد الترتيبية: حيث كل رقم طبيعي له خَلَفْ وكل رقم طبيعي غير صفري له سَلَفْ متفرد. مسلمات بيانو مُكافِئَة للعديد من نظم نظرية المجموعات الضعيفة. أحد هذه الأنظمة هو ZFC مع استبدال بديهية اللانهاية (Axiom of infinity) بما ينفيها. نظرية جودشتاين (Goodstein's theorem) من النظريات التي يمكن إثباتها في ZFC ولا اثبات لها بمسلمات بيانو.[20]

في هذه التعريفات، يسهل إدراج 0 (ويقابله المجموعة الخالية) كرقم طبيعي. إدراج 0 هو الآن تقليد متعارف عليه بين علماء نظرية المجموعات[21] والمنطقيين.[22] وكذا يدرج علماء الرياضيات الآخرون الصفر[arabic-abajed 1] ولغات الحاسوب أيضًا تستخدم نظم عد تبدأ بالصفر عند تعداد العناصر كـ عدادات الحلقات وعناصر السلسلة أو المصفوفات.[23][24] لكن على الجانب المقابل، تمسك كثيرون من علماء الرياضيات بالتقاليد القديمة معتبرين 1 أول رقم طبيعي.[25]

يستخدم علماء الرياضيات الرمز N أو ${\displaystyle \mathbb {N} }$ للإشارة إلى مجموعة الأعداد الطبيعية.[26][27] التي أسستها نظرية المجموعات. أحيانا استخدم الرمز J في الكتابات القديمة للإشارة لهذه المجموعة.[28]

ونظرًا لأن العنصرين 0 و 1 لهما خصائص مميزة (كعناصر محايدة للجمع والضرب، على التوالي)، فمن المهم معرفة نوع الأرقام الطبيعية المستخدم. يمكن ذلك عن طريق الشرح داخل النص (بكتابة عناصر المجموعة)، أو بوضع علامة علوية أو منخفضة،[29][30] كالمثال التالي:

• الأعداد الطبيعية بدون الصفر: ${\displaystyle \{1,2,...\}=\mathbb {N} ^{*}=\mathbb {N} ^{+}=\mathbb {N} _{0}\smallsetminus \{0\}=\mathbb {N} _{1}}$
• الأعداد الطبيعية مع الصفر: ${\displaystyle \;\{0,1,2,...\}=\mathbb {N} _{0}=\mathbb {N} ^{0}=\mathbb {N} ^{*}\cup \{0\}}$

بشكل آخر ونظرًا لأن الأعداد الطبيعية تشكل طبيعيًا مجموعة جزئية من الأعداد الصحيحة (غالبًا ما يرمز لها بـ ${\displaystyle \mathbb {Z} }$), لذا يمكن الإشارة إليها على أنها الأعداد الصحيحة الموجبة أو غير السالبة.[31] لتوضيح إذا كان الرقم 0 مدرجًا أم لا، يتم أحيانًا إضافة حرف سفلي (أو علوي) "0" في الحالة الأولى (الأعداد الموجبة)، ويتم إضافة حرف علوي "*" في الحالة الأخيرة (غير السالبة):[29]

${\displaystyle \{1,2,3,\dots \}=\{x\in \mathbb {Z} :x>0\}=\mathbb {Z} ^{+}=\mathbb {Z} _{>0}}$

${\displaystyle \{0,1,2,\dots \}=\{x\in \mathbb {Z} :x\geq 0\}=\mathbb {Z} _{0}^{+}=\mathbb {Z} _{\geq 0}}$

الطريقة الأكثر بساطة، والأكثر سهولة من حيث الفهم، من أجل تحديد أولية عدد ما تدعى القسمة المتكررة.

خوارزمية بسيطة لعالم رياضيات اليونانية إراتوستينس لإيجاد جميع الأعداد الأولية حتى العدد 120. (انقر لرؤية الرسوم المتحركة).

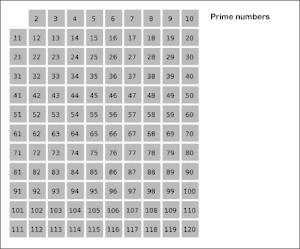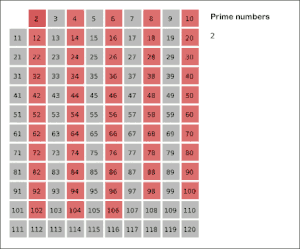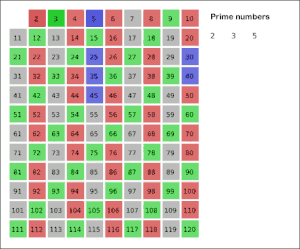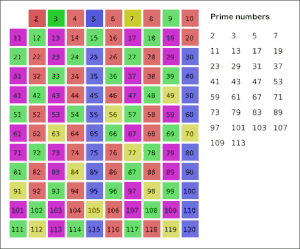
كل خوارزمية تمكن من إيجاد جميع الأعداد الأولية الأصغر من عدد ما تسمى غربالا. أقدم مثال على ذلك غربال إراتوستينس لكنه لا يستعمل إلا في حالة الأعداد الصغيرة. غربال أتكين أحدث منه ولكنه أكثر منه تعقيدا ولهذا فهو أكثر منه سرعة.

مبرهنة فيرما الصغرى تبين أنه إذا كان p عددا أوليا وa عددا أوليا مع p، إذن:${\displaystyle a^{p-1}\equiv 1\ \ (p)}$

عكس المبرهنة خاطئ، مثلا 561=3×11×17 ليس عددا أوليا ومع ذلك بالنسبة لعدد a أولي مع 561، لدينا ${\displaystyle a^{560}\equiv 1\ \ (561)}$

لكن يمكن مع ذلك كتابة:

إذا كان p غير أولي فإن ${\displaystyle a^{p-1}}$ متوافق مع 1 بترديد p لقيمة ما a

الشيء الذي يمثل عكس احتمالي للمبرهنة.

برمجة التشفير PGP، تستعمل هذه الخاصية لمعرفة إذا كانت الأعداد العشوائية التي يختارها أعداد أولية. إذا كان: ${\displaystyle 1\equiv 2^{x-1}\equiv 3^{x-1}\equiv 5^{x-1}\equiv 7^{x-1}\ \ (x)}$، فهذا يعني أن x عدد أولي احتمالي.

إذا أعطت إحدى المعادلات قيمة مخالفة ل1، في هذه الحالة x عدد غير أولي قطعيا.

الطريقة الأكثر بساطة، والأكثر سهولة من حيث الفهم، من أجل تحديد أولية عدد ما تدعى القسمة المتكررة.

ppcm (4;9) = 36 ppcm (6;10)=30

ليكن a و b عددين صحيحين طبيعيين غير منعدمين القاسم المشترك الأكبر للعددين a و b هو اآكبر قاسم مشترك لهما نرمز له بالرمز pgcd مثال:

pgcd(126;90)=18 pgcd(4;9)=1

• طريقة لتحديد المضاعف المشترك الأصغر للعددين a و b حيث a>b

أحدد مضاعفات a ثم أتآكد بالتتابع ابتداء من أصغر مضاعف غير منعدم للعدد a هل هو مضاعف للعدد b، فإذا آان الجواب لا، أتابع البحث إن آان نعم، أتوقف والعدد الذي حصلت فيه على هذا الجواب هو المضاعف المشترك الأصغر للعددين a و b.

• • طريقة لتحديد القاسم المشترك الآكبر للعددين a و b حيث a>b

أحدد قواسم العدد b ثم أتآكد بالتتابع تناقصيا ابتداء من أكبر قاسم للعدد b هل هو قاسم للعدد a فإذا آن الجواب لا، أتابع البحث ان كان نعم، أتوقف والعدد الذي حصلت فيه على هذا الجواب هو القاسم المشترك الأكبر للعددين a و b.

• • • طريقة لتحديد ما إذا كان العدد a أوليا أم لا

نحدد أولا جميع الأعداد الأولية p حيث p×p<a -إذا كان a يقبل القسمة على أحد هذه الأعداد فان a غير أولي -إذا كان a لا يقبل القسمة على أي عدد من هذه الأعداد فان a أولي