تكامل عددي

في التحليل العددي، يشكل التكامل العددي عائلة واسعة من الخوارزميات لحساب القيمة العددية لتكامل محدد، وللتوسع أكثر يستعمل المصطلح أحيانا أيضا في وصف الحل العددي للمعادلات التفاضلية.

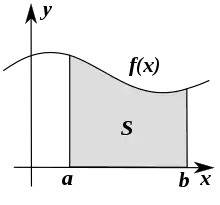
تكامل عددي يتكون من إيجاد تقريبات عددية للقيمة

S\,

في بعض الأحيان ما ينسب التكامل التربيعي (يختصر عادة التربيعي) كمعنى للتكامل العددي، وخاصة عند تطبيقه على التكاملات الأحادية.[1][2][3] كما يطلق مصطلح التكعيبي عادة على التكاملات الثنائية فما فوقها.

المسألة الأساسية التي يمكن اعتبارها في التكامل العددي هي حساب حل تقريبي لتكامل محدد:

\int _{a}^{b}\!f(x)\,dx.

تاريخ

التربيع هو مصطلح رياضي تاريخي الذي يعني حساب المنطقة. مشاكل التربيع تعتبر واحدة من المصادر الرئيسية للتحليل الرياضي في اليونان القديمة، وفقا لمذهب فيثاغورس، فهم حساب المنطقة في عملية بناء هندسي مربع وجود نفس المنطقة (تربيع). هذا هو السبب سميت عملية التربيع. على سبيل المثال، التربيع من الدائرة، تاسا أبقراط، والتربيع من القطع المكافئ. يجب أن يتم تنفيذ هذا البناء عن طريق البوصلة ومستقيمة. للتربيع مستطيل مع الجانبين أ وب من الضروري لبناء مربع مع الجانب

$x={\sqrt {ab}}$

لهذا الغرض فمن الممكن استخدام الحقيقة التالية: إذا نرسم دائرة من مجموع أ وب كقطر، ثم ارتفاع BH (من نقطة التقاطعهم الي التقاطع مع الدائرة) يساوي متوسطها الهندسي. بناء هندسي مماثل يحل مشكلة التربيع لمتوازي الأضلاع والمثلث. مشاكل التربيع لأرقام منحنية أكثر صعوبة بكثير. وقد ثبت في القرن 19أن التربيع من الدائرة مع البوصلة وحافة مستقيمة يكون مستحيلا.

ومع ذلك، بالنسبة لبعض الأرقام (على سبيل المثال تاسا أبقراط) التربيع لا يمكن أن يؤديها.

أصبحت التربيع من سطح الكرة وشريحة القطع المكافئ الذي قام به أرخميدس أعلى إنجاز تحليل العتيقة.

مساحة سطح الكره تساوي أربع أضعاف مساحة الدائرة العظمى لهذه الكره
مساحة الجزء من القطع المكافئ المقطوع منه بخط مستقيم يساوي 4\3 من مساحة المثلث المحتوى بهذا الجزء

لإثبات هذه النتائج، استخدم ارشميديس طريقة استنفاد إكسوديس.

في أوروبا العصور الوسطى، التربيع كان يعني حساب المساحة بأي طريقة. كما أن طريقة الغير قابلين للقسمة كانت تستخدم. رغم أنها كانت غير دقيقة إلا انها كانت سهلة وقوية. بمساعدتها إستطلع جاليليو جاليله وجيلز دي روبرفال حساب مساحة قوس دوروية، واستطاع جيرجوار دي سانت فنسنت حساب المساحة تحت الغلو (Opus Geometricum, 1647). واستطاع البوس أنطونيو دي ساراسا، تلميذ ومعلق دي سانت فنسنت، ملاحظة علاقة هذه المساحة باللوغاريتمات.

قام جون وليس بتحويل هذه النظرية لمعادلات جبرية: حيث كتب سلسلته Arithmetica Infinitorum عام 1647 التي نطق عليها الآن اسم التكاملات المحددة، كما استطاع أن يحدد قيمها. إسحاق بارو وجايمس جرجوري قاما بتطور أبعد: تربيعات لأقواس وحلزونات جبرية. واستطاع كريستيان هيجينز بنجاح عمل تربيعات لبعض مجسمات الثورة.

تربيعات الغلو التي قام بحسابها دي سانت فنسنت ودي سارسا أدت إلى استحداث دالة جديدة، اللوغاريتم الطبيعية، الهامة للغاية.

مع اختراع حساب التفاضل والتكامل ظهرت طريقة عالمية لحساب المساحات. كنتيجة، أصبحت كلمة تربيع كلمة تراثية، وكبديل استخدمت عبارة «حساب المتغير الأوحد التكاملي المحدد» بشكل أوسع.

أسباب اللجوء للتكامل العددي

توجد أسباب عدة للجوء للتكامل العددي. فالكمية المتكاملة $f(x)\,$ يمكن معرفتها فقط عند نقاط معينة، كتلك المحصل عليها عن طريق الأخذ بالعينة. بعض الأنظمة المضمنة وبعض التطبيقات الأخرى قد تحتاج إلى تكامل عددي لهذا السبب.

قد يعرف المرء الكمية المتكاملة ولكن يكون من الصعب أو المستحيل إيجاد الاشتقاق العكسي والذي يفترض أن يكون دالة أساسية. مثال ذلك هو $f(x)=e^{-x^{2}}$ ، والتي لايمكن كتابة اشتقاقها العكسي بصورة أولية.

قد يكون ممكننا إيجاد الاشتقاق العكسي بشكل رمزي، ولكن ربما كان حساب التقريب العددي أسهل من إيجاد الاشتقاق العكسي. قد تكون تلك الحالة عندما يعطى الاشتقاق العكسي في صورة متسلسلة لانهائية، أو إذا كان تقديرها يتطلب دالة خاصة غير متوافرة.

طرق التكامل ذات البعد الواحد

طرق حساب التكامل العددي يمكن وصفها بشكل عام على أنها تقييمات مجموعة للكميات المتكاملة للحصول على قيمة تقريبية للتكامل. الكميات المتكاملة تحسب عند مجموعة معروفة من النقط تدعى نقاط التكامل والمجموع الموزون لهذه النقط يستعمل في تقريب التكامل. نقاط التكامل والأوزان تعتمد على طريقة معينة والدقة تستنتج من التقريب. جزء هام من تحليل أي طريقة من تكامل العددي هو دراسة خطأ التقريب كمعادلة في عدد التكاملات. وعادة ما تعتبر الطريقة التي ينتج خطأ صغير لعدد قليل من التقييمات أفضل. تخفيض عدد التقييمات من الكمية المتكاملة يقلل من عدد من العمليات الحسابية وبالتالي يقلل من إجمالي الخطأ. أيضا، كل حساب قد يستغرق وقتا طويلا، والكمية المتكاملة قد تكون معقدة جدا.

'brute force' نوع من التكامل العددي يمكن القيام به إذا كانت الكمية المتكاملة حسنة التصرف، من خلال تقييم الكمية المتكاملة مع زيادات صغيرة جدا.

قواعد التربيع على أساس معادلات التحريف

هناك فئة كبيرة من قواعد التربيع يمكن استخلاصها عن طريق إنشاء معادلات التحريف التي هي سهلة التكامل. عادة معادلات التحريف هي متعددة الحدود. في الممارسة العملية، بما أن متعددة الحدودالتي تكون من درجة عالية جدا تميل إلى التأرجح بصورة عشوائية لذلك تستخدم متعددة الحدود ذات درجة منخفضة، عادة الخطية والتربيعية. أبسط طريقة لهذا النوع هو السماح لمعادلة التحريف بأن تكون معادلة ثابتة (متعدد الحدود من الدرجة صفر) الذي يمر عبر نقطة ((a+b)/2, f((a+b)/2))، وهذا ما يسمى قاعدة نقطة المنتصف أو قاعدة المستطيل.

\int _{a}^{b}f(x)\,dx\approx (b-a)\,f\left({\frac {a+b}{2}}\right)

معادلة التحريف قد تكون خط مستقيم (أي متعدد الحدود من الدرجة الأولى) تمر عبر النقط ((a, f(a) و ((b, f(b). وهذا ما يسمى بقاعدة شبه المنحرف:

\int _{a}^{b}f(x)\,dx\approx (b-a)\,{\frac {f(a)+f(b)}{2}}.

بأي واحدة من هذه القواعد، يمكننا أن نجعل التقريب أكثر دقة عن طريق تقسيم الفترة [a, b] إلى بعض الفترات الصغيرة وحساب تقريب لكل فترة صغيرة ثم يتم تجميع كل النتائج. وهذا ما يسمى بقاعدة المركبة. على سبيل المثال، يمكن القول قاعدة شبه منحرف المركبة:

\int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{n}}\left({f(a) \over 2}+\sum _{k=1}^{n-1}\left(f\left(a+k{\frac {b-a}{n}}\right)\right)+{f(b) \over 2}\right)

حيث الفترات الثانوية تاخذ شكل [k h, (k+1) h]في حين h = (b−a)/n و k = 0, 1, 2, ..., n−1. الاستيفاء مع متعددو الحدود المقيمة في نقاط متباعدة بالتساوي في الفترة ما بين [a, b] تعطي صيغ نيوتن-كوتس الذي من امثلاتها قاعدة المستطيل وقاعدة شبه المنحرف. قاعدة سمبسون التي تعتمد علي متعددة حلول من الدرجة الثانية تعد أيضا من صيغ نيوتن-كوتس. قواعد التربيع مع نقاط متباعدة بالتساوي تملك خاصية ملائمة جدا للتداخل. القاعدة المقابلة مع كل فترة مقسمة تشمل جميع النقط الحالية، حيث يمكن إعادة استخدام تلك القيم التكاملية. إذا سمحنا للفترات الفاصلة بين نقاط الاستيفاء بالتفاوت، نجد مجموعة أخرى من صيغ التربيع، مثل صيغ غاوس التربيعية. قاعدة غاوس التربيعية عادة أكثر دقة من قاعدة نيوتن-كوتس، الامر الذي يتطلب نفس العدد من تقيمات الدالة، إذا كان التكامل سلس (أي، إذا كان ذلك مختلف بما فيه الكفاية).تشمل اساليب أخرى للتربيع مع فترات متفاوتة طريقة كلنشو-كيرتس للتربيع (أيضا تسمى طريقة فيرر للتربيع) التي تسمح بالتداخل. قواعد غاوس للتربيع لا تسمح بالتداخل ولكن صيغ غاوس-كرونورد للتربيع ذات الصلة تسمح بذلك.

طرق للتكاملات الأحادية

خوارزميات متلائمة

def calculate_definite_integral_of_f(f, initial_step_size):
    '''
    This algorithm calculates the definite integral of a function
    from 0 to 1, adaptively, by choosing smaller steps near
    problematic points.
    '''
    x = 0.0
    h = initial_step_size
    accumulator = 0.0
    while x < 1.0:
        if x + h > 1.0:
            h = 1.0 - x
        quad_this_step = 
        if error_too_big_in_quadrature_of_over_range(f, [x,x+h]): 
            h = make_h_smaller(h)
        else:
            accumulator += quadrature_of_f_over_range(f, [x,x+h])
            x += h
            if error_too_small_in_quadrature_of_over_range(f, [x,x+h]): 
                h = make_h_larger(h) # Avoid wasting time on tiny steps.
    return accumulator

برنامج للتكامل العددي

Numerical integration is one of the most intensively studied problems in numerical analysis. Of the many software implementations we list a few here.

QUADPACK (part of SLATEC): description , source code . QUADPACK is a collection of algorithms, in Fortran, for numerical integration based on Gaussian quadrature.
GSL: The GNU Scientific Library (GSL) is a numerical library written in C which provides a wide range of mathematical routines, like Monte Carlo integration.
Numerical integration algorithms are found in GAMS class H2.
ALGLIB is a collection of algorithms, in C# / C++ / Delphi / Visual Basic / etc., for numerical integration (includes Bulirsch-Stoer and Runge-Kutta integrators).

المراجع

"معلومات عن تكامل عددي على موقع id.ndl.go.jp"، id.ndl.go.jp، مؤرشف من الأصل في 27 أبريل 2020.
"معلومات عن تكامل عددي على موقع babelnet.org"، babelnet.org، مؤرشف من الأصل في 15 ديسمبر 2019.
"معلومات عن تكامل عددي على موقع jstor.org"، jstor.org، مؤرشف من الأصل في 27 مايو 2019.

فيليب جاي ديفيس and Philip Rabinowitz, Methods of Numerical Integration.
جورج فورسيث، Michael A. Malcolm, and كليف مولير، Computer Methods for Mathematical Computations. Englewood Cliffs, NJ: Prentice-Hall, 1977. (See Chapter 5.)
Press, W.H.؛ شاول تيوكولسكي, S.A.؛ Vetterling, W.T.؛ Flannery, B.P. (2007)، "Chapter 4. Integration of Functions"، Numerical Recipes: The Art of Scientific Computing (ط. 3rd)، New York: Cambridge University Press، ISBN 978-0-521-88068-8
Josef Stoer and Roland Bulirsch, Introduction to Numerical Analysis. New York: Springer-Verlag, 1980. (See Chapter 3.)
كارل بنجامين بوير، A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach, New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7).
Eves, Howard, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0,

بوابة رياضيات
بوابة تحليل رياضي

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] "معلومات عن تكامل عددي على موقع id.ndl.go.jp"، id.ndl.go.jp، مؤرشف من الأصل في 27 أبريل 2020.

[2] "معلومات عن تكامل عددي على موقع babelnet.org"، babelnet.org، مؤرشف من الأصل في 15 ديسمبر 2019.

[3] "معلومات عن تكامل عددي على موقع jstor.org"، jstor.org، مؤرشف من الأصل في 27 مايو 2019.