دالة سينك

في الرياضيات والفيزياء والهندسة التطبيقية، دالة سينك أو دالة الجيب الجوهري (بالإنجليزية: Sinc function)‏، التي يرمز إليها بـ $sinc(x)$ ، لها تعريفان مختلفان قليلاً.[1]

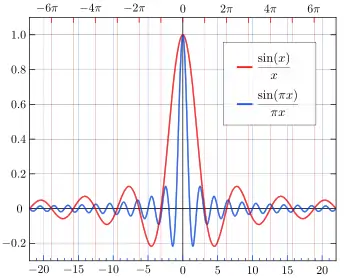
تظهر دالتي سينك المعيارية (بالأزرق) والغير معيارية (بالأحمر) على نفس المقياس

في الرياضيات، دالة سينك غير المعيارية التاريخية معرفة من أجل $x \neq 0$ بواسطة:

\operatorname {sinc} (x)={\frac {\sin(x)}{x}}.

بدلاً من ذلك، غالبًا ما تسمى دالة سينك غير المعيارية بـ«دالة المعاينة»، يشار إليها بـ $Sa(x)$ .[2]

في المعالجة الرقمية للإشارة ونظرية المعلومات، تعرّف دالة سينك المعيارية بشكل شائع من أجل $x \neq 0$ بواسطة:

\operatorname {sinc} (x)={\frac {\sin(\pi x)}{\pi x}}.

في كلتا الحالتين، تعرّف القيمة عند $x = 0$ على أنها قيمة النهاية التالية:

\operatorname {sinc} (0):=\lim _{x\to 0}{\frac {\sin(ax)}{ax}}=1

من أجل كل عدد حقيقي

a \neq 0

.

يؤدي التعيير ^{[الإنجليزية]} إلى تكامل محدد للدالة على الأعداد الحقيقية ليساوي 1 (في حين أن نفس التكامل لدالة سينك غير المعيارية له قيمة $π$ ). كخاصية مفيدة أخرى، فإن جذور دالة سينك المعيارية هي القيم الصحيحة غير الصفرية لـ x.

دالة سينك المعيارية هي تحويل فورييه للدالة المستطيلية بدون تدريج.

الفرق الوحيد بين التعريفين هو في تدريج المتغير المستقل (محور $x$ ) بواسطة العامل $π$ . في كلتا الحالتين، يُفهم أن قيمة الدالة عند التفرد القابل للإزالة عند الصفر هي قيمة النهاية 1. ثم تُحلل دالة سينك في كل مكان ومن ثم دالة كاملة.

أدخل المصطلح sinc من قبل فيليب وودوارد ^{[الإنجليزية]} في مقالته "Information theory and inverse probability in telecommunication" صدرت عام 1952، قال فيها إن الدالة «تظهر كثيرًا في تحليل فورييه وتطبيقاتها لدرجة أنها تستحق بعضًا من الترميزات الخاص بها»،[3] وهي كتابه Probability and Information Theory, with Applications to Radar صدر عام 1953.[4][5]

مراجع

Olver؛ Daniel M, Lozier؛ Ronald F, Boisvert؛ Charles W., Clark (2010)، Numerical methods (باللغة الإنجليزية)، Cambridge University press، ISBN 978-0-521-19225-5، مؤرشف من الأصل في 08 فبراير 2020. {{استشهاد بكتاب}}: الوسيط |مؤلف2= و|الأخير2= تكرر أكثر من مرة (مساعدة)
Singh, R. P.؛ Sapre, S. D. (2008)، Communication Systems, 2E (ط. illustrated)، Tata McGraw-Hill Education، ص. 15، ISBN 978-0-07-063454-1، مؤرشف من الأصل في 24 يوليو 2020. Extract of page 15
Woodward, P. M.؛ Davies, I. L. (مارس 1952)، "Information theory and inverse probability in telecommunication" (PDF)، Proceedings of the IEE - Part III: Radio and Communication Engineering، 99 (58): 37–44، doi:10.1049/pi-3.1952.0011، مؤرشف من الأصل (PDF) في 24 يوليو 2020.
Poynton, Charles A. (2003)، Digital video and HDTV، Morgan Kaufmann Publishers، ص. 147، ISBN 978-1-55860-792-7، مؤرشف من الأصل في 5 أغسطس 2020.
Woodward, Phillip M. (1953)، Probability and information theory, with applications to radar، London: Pergamon Press، ص. 29، ISBN 978-0-89006-103-9، OCLC 488749777، مؤرشف من الأصل في 5 أغسطس 2020.

بوابة رياضيات
بوابة تحليل رياضي
بوابة الفيزياء

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Olver؛ Daniel M, Lozier؛ Ronald F, Boisvert؛ Charles W., Clark (2010)، Numerical methods (باللغة الإنجليزية)، Cambridge University press، ISBN 978-0-521-19225-5، مؤرشف من الأصل في 08 فبراير 2020. {{استشهاد بكتاب}}: الوسيط |مؤلف2= و|الأخير2= تكرر أكثر من مرة (مساعدة)

[2] Singh, R. P.؛ Sapre, S. D. (2008)، Communication Systems, 2E (ط. illustrated)، Tata McGraw-Hill Education، ص. 15، ISBN 978-0-07-063454-1، مؤرشف من الأصل في 24 يوليو 2020. Extract of page 15

[3] Woodward, P. M.؛ Davies, I. L. (مارس 1952)، "Information theory and inverse probability in telecommunication" (PDF)، Proceedings of the IEE - Part III: Radio and Communication Engineering، 99 (58): 37–44، doi:10.1049/pi-3.1952.0011، مؤرشف من الأصل (PDF) في 24 يوليو 2020.

[Poynton-4] Poynton, Charles A. (2003)، Digital video and HDTV، Morgan Kaufmann Publishers، ص. 147، ISBN 978-1-55860-792-7، مؤرشف من الأصل في 5 أغسطس 2020.

[5] Woodward, Phillip M. (1953)، Probability and information theory, with applications to radar، London: Pergamon Press، ص. 29، ISBN 978-0-89006-103-9، OCLC 488749777، مؤرشف من الأصل في 5 أغسطس 2020.