دالة مربع
دالة مربع عدد هي الدالة التي تحول العدد إلى مربعه.
| الدالة مربع | |
|---|---|
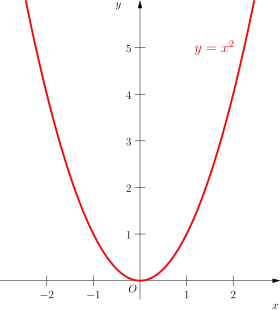 الرسم البياني لدالة مربع له شكل قطع مكافئ. الرسم البياني لدالة مربع له شكل قطع مكافئ. | |
| تدوين | |
| دالة عكسية | |
| مشتق الدالة | |
| مشتق عكسي (تكامل) |
|
| الميزات الأساسية | |
| زوجية أم فردية؟ | زوجية |
| مجال الدالة | |
| المجال المقابل | |
| قيم محددة | |
| القيمة/النهاية عند الصفر | 0 |
| نهاية الدالة عند +∞ | |
| نهاية الدالة عند -∞ | |
| الحدود الأدنى | 0 |
| القيمة/النهاية عند 1 | 1 |
| القيمة/النهاية عند 2 | 4 |
| القيمة/النهاية عند -1 | 1 |
| القيمة/النهاية عند -2 | 4 |
| جذور الدالة | 0 |
| نقاط حرجة | 0 |
| نقاط ثابتة | 1 و0 |
خصائص
إشارة
الخاصية الأولى هي إيجابية الدالة مربع. في الواقع، من أجل كل عدد حقيقي ، فإن هو جداء عددين حقيقيين لنفس الإشارة؛ حسب قاعدة الإشارات فإنها موجبة.
زوجية
تعتبر الدالة مربع دالة زوجية أي : من أجل كل عدد حقيقي . في الواقع، مع الملاحظة السابقة بتطبيق قاعدة الإشارات نتحصل على: .
دالة عكسية
دالة عكسية لـ على المجال هي دالة الجذر التربيعي .
حل معادلة من الشكل
حساب سوابق العدد الحقيقي a بواسطة الدالة مربع يكافئ حل المعادلة . هناك ثلاث حالات ممكنة :
- : ليس للمعادلة حل في مجموعة الأعداد الحقيقية.
- : للمعادلة حل وحيد، x = 0 ؛
- : للمعادلة حلان، و .
التكامل
بما أن الدالة مربع هي عبارة عن كثير حدود تربيعي، فإن طريقة سيمبسون تكون دقيقة عندما نحسب تكاملها. من أجل كل متعدد الحدود التربيعي P والأعداد الحقيقية a و b، لدينا:
إذن، من أجل لدينا :
مراجع
- بوابة رياضيات
- بوابة تحليل رياضي
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.