دوران نجمي
دوران النجم أو لف النجوم (بالإنجليزية: Stellar rotation) هي الحركة الزاوية للنجم حول محوره. ويمكن قياس معدل الدوران من طيف النجم، أو عن طريق توقيت حركات الملامح الفعالة على سطح النجم.

دوران النجم ينتج عنة انتفاخ عند خط استوائه بسبب قوة الطرد المركزي وبما ان النجوم ليست أجسام صلبة، فهي تخضع لدوران تفاضلي. في هذة الحالة فأن خط الاستواء للنجم يمكن أن يدور بسرعات زاوية مختلفة عن مناطق خطوط العرض العليا.وقد يكون لهذه الاختلافات في معدل الدوران داخل نجم دورا هاما في توليد المجال المغناطيسي النجمي.[1]
القياس
يعتمد معدل دوران النجم على عمرة وكتلتة لأن معدل دوران النجوم تتباطأ بشكل ثابت مع الزمن ويعتقد علماء الفلك أن النجوم الأكبر والأثقل تميل لتدور أسرع من النجوم الأصغر والأخف ولقياس دوران النجم حول نفسه يبحث الفلكيون عن التغير في سطوع النجم. والناتجة عن البقع المظلمة الموجودة فوق سطحه –المكافئ النجمي للبقع الشمسية [2]
وما لم يتم رصد النجم من اتجاه القطب، فأن أجزاء من سطح النجم لها قدر من الحركة نحو أو بعيدا عن المراقب. ويطلق على عنصر الحركة التي هي في اتجاه المراقب السرعة الشعاعية.لاجزاء السطح التي لديها سرعة شعاعية في اتجاه المراقب فأن الإشعاع يتحول إلى تردد أعلى بسبب تأثير دوبلر وبالمثل تنزاح المناطق المبتعدة عن المراقب إلى تردد أدنى.عند مراقبة خطوط الطيف النجمية، هذا التحول في نهايتي الطيف يؤدي إلى توسع الخط.[3] ومع ذلك، هذا التوسيع يجب فصله بعناية عن الآثار الأخرى التي يمكن أن تزيد من عرض الخط.
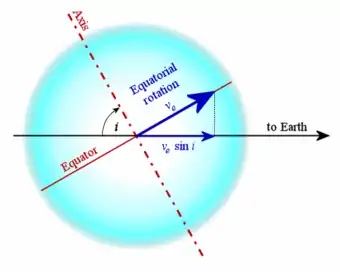
مكون السرعة الشعاعية المرصود من خلال توسيع الخط يعتمد على ميل قطب النجم إلى خط الرؤية. وتعطى القيمة المشتقة كالتالي: , حيث ve هي سرعة الدوران عند خط الاستواء و i هو الميل.ومع ذلك، i ليس معروف دائما، وبالتالي فإن النتيجة تعطي قيمة الحد الأدنى لسرعة دوران النجم.هذا إذا كان i ليس زاوية قائمة عندها السرعة الفعلية تكون أكبر من .[3] ويشار إلى هذاأحيانا بسرعة الدوران المتوقعة.
في حالة النجوم العملاقة اضطراب ضئيل في الغلاف الجوي يمكن أن يؤدي إلى تعريض الخط الذي هو أكبر بكثير من آثار الدوران متسببا باخفاء الإشارة. ومع ذلك، هناك طريقة أخرى لمعالجة المشكلة من خلال الاستفادة من تأثير العدسية الصغرية الجذبية يحدث هذا عندما يمر جسم ضخم أمام نجم أبعد، ويتصرف كعدسة، ومكبرا الصورة لفترة قصيرة. المعلومات الأكثر تفصليا التي يتم جمعها خلال هذا الحدث، تجعل من الأسهل التميز بين تأثير الاضطراب الضئيل في الغلاف الجوي والدران.[4]
وعلاوة على ذلك، إذا أظهر النجم نشاطا على السطح، مثل البقع النجمية، هذه الميزة يمكن أن تستخدم لتقدير فترة الدوران. ومع ذلك، يمكن لهذه البقع ان تتشكل في مواقع مختلفة من خط الاستواء ثم تهاجر على طول خطوط العرض المختلفة على مدى فترة حياتها، لذلك فأن الدوران التفاضلي للنجم يمكن أن ينتج قياسات متفاوتة جدا. وكثيرا ما يرتبط النشاط المغناطيسي النجمي مع الدوران السريع، لذلك هذه التقنية يمكن استخدامها لقياس امثال هذة النجوم.[5] وقد أظهرت دراسة البقع النجمية انها من الممكن أن تسبب بالاختلاف في معدل سرعة دوران النجم حيث يقوم الحقل المغناطيسي بتعديل تدفق الغازات في النجم.[6]
الآثار المادية
الانتفاخ الاستوائي
تميل الجاذبية إلى تشكيل الأجرام السماوية على شكل كرة مثالية، شكل تكون فيه كل الكتلة أقرب ما يمكن إلى مركز الثقل لكن النجم الدوار ليس كروي الشكل، ولديه انتفاخ استوائي. ان دوران قرص نجم أولي يتقلص ليشكل شكل النجم ليصبح أكثر وأكثر كروية، ولكن هذا التقلص لا يمضي حتى النهاية ليشكل كرة مثالية.حيث تعمل الجاذبية في القطبين على زيادة الانكماش، ولكن عند خط الاستواء يتناقص مفعول الجاذبية بسبب اثر قوة الطرد المركزي. الشكل النهائي للنجم بعد تكون النجم هو شكل متوازن.بمعنى أن الجاذبية الفعالة في المنطقة الاستوائية (التي تضاءلت) لا يمكن ان تسحب النجم إلى شكل أكثر كروية. كما يؤدي الدوران إلى ارتفاع تعتيم الجاذبية [معلومة 1] عند خط الاستوا، كما تصفها نظرية فون زايفول.
نجم المليك ("ألفا الأسد") هو مثال صارخ على الانتفاخ الاستوائي للنجوم حيث تقدر سرعة الدوران عند خط الاستواء لهذا النجم 317 ± 3 كم / ث. وهذا يتوافق مع فترة دوران تعادل 15.9 ساعة وتساوي 86٪ من السرعة التي قد يتفكك عندها النجم.القطر الاستوائي لهذا النجم أكبر بحوالي 32٪ من القطر القطبي.[7] وبين النجوم سريعة الدوران بلييوني-النسر الواقع-الظليم ويعتبر نجم الظليم أقل النجوم من حيث الشكل الكرى في درب التبانة [8]
سرعة تفكك نجم هي تعبير يستخدم لوصف الحالة التي تكون فيها قوة الطرد المركزي عند خط الاستواء مساوية لقوة الجاذبية.وليكون نجم مستقر يجب أن تكون سرعة الدوران أقل من هذه القيمة.[9]
الدوران التفاضلي
يلاحظ الدوران التفاضلي لسطح نجم مثل الشمس عندما تختلف السرعة الزاوية في خطوط العرض. عادة السرعة الزاوية تتناقص مع زيادة العرض. ولكن لوحظ عكس ذلك، مثال على ذلك النجم HD 31993 .[10][11] وأول هذه النجوم، غير الشمس، لة خرائط مفصلة لدورانة التفاضلي هو النجم AB Doradus [1][12] الآلية الأساسية التي تسبب الدوران التفاضلي هي الحمل الحراري المضطرب داخل النجوم. حركة الحمل الحراري تحمل الطاقة نحو السطح من خلال حركة كتلة البلازما.. هذا الكم الهائل من البلازما يحمل جزء من السرعة الزاوية للنجم. عندما يحدث الاضطراب خلال القص والتدوير، الزخم الزاوي يمكن أن يتوزع على خطوط العرض المختلفة خلال تدفق من الشمال إلى الجنوب أو تدفق من الجنوب إلى الشمال (تدفق خط-طولي).[13][14]
ويعتقد السطح البيني في المناطق ذات الاختلافات في معدل الدوران داخل النجم دورا هاما في توليد المجال المغناطيسي النجمي.[1]
كبح التدوير
خلال التشكل
| التصنيف النجمي |
ve (كم/ثانية) |
|---|---|
| O5 | 190 |
| B0 | 200 |
| B5 | 210 |
| A0 | 190 |
| A5 | 160 |
| F0 | 95 |
| F5 | 25 |
| G0 | 12 |
يعتقد أن النجوم تتكون نتيجة لانهيار سحابة من الغاز والغبار ذات درجات حرارة منخفضة.اثناء انهيار السحابة تؤدي كمية الحركة الزاوية إلى ازدياد أي احبولة صغيرة في السحابة. مما يجعل مواد القرص تدور. وفي هذا المركز الكثيف للقرص تتشكل النجوم الأولية التي تكتسب الحرارة من طاقة وضع الانهيار.
مع استمر الانهيار، يمكن أن يزداد معدل الدوران إلى النقطة التي يتفكك فيها النجم الأولي بسبب قوة الطرد المركزي عند خط الاستواء. وبالتالي يجب كبح معدل الدوران خلال ال 100,000 سنة الأولى لتجنب هذا السيناريو.أحد التفسيرات المحتملة للكبح هو تفاعل المجال المغناطيسي للنجم الاولي مع الريح النجمية خلال الكبح المغناطيسي[معلومة 2] الرياح المتوسعة تحمل الزخم الزاوي بعيدا وتبطئ معدل الدوران الانهياري للنجم الاولي [16][17]
معظم نجوم النسق الأساسي في الفئة الطيفية بين O5 وF5 تم العثور عليها تدور بسرعة.[7][18]
بعد التشكل
لنجوم النسق الأساسي انخفاض التدوير يمكن تمثيلة من خلال العلاقة الرياضية:
حيث هي السرعة الزاوية في خط الاستواء وt عمر النجم.[19] تدعى هذه العلاقة بقانون Skumanich نسبة إلى أندرو P. Skumanich الذي اكتشفها في عام 1972 [20][21] ولكن في الواقع قد اقترحت هذة العلاقة في وقت سابق بكثير من قبل Evry Schatzman.[22]
دراسة الدوران الزمني (gyrochronology)[معلومة 3] هي الوسيلة لتقدير عمر النجم على أساس معدل الدوران، باستخدام الشمس كمعيار.حيث يعتمد معدل دوران النجم حول نفسه على عمره لأنه يتباطأ بشكلٍ منتظم مع مرور الزمن [23]
تفقد النجوم كتلتها ببطء بسبب انبعاث الرياح النجمية من خلال الغلاف الضوئي أو الطبقة الضوئية للنجم وهي الجزء الخارجي المشع للضوء.ويقوم المجال المغناطيسي للنجم يمارسة عزم الدوران حول مسألة انبعاث الرياح النجمية، مما يؤدي إلى نقل ثابت الزخم الزاوي بعيدا عن النجم. النجوم التي لها معدل دوران أكبر من 15 كم/ثانية تظهر فقدان كتلة أسرع، وبالتالي معدل أسرع في تضاؤل سرعة الدوران.وهكذا مع تباطؤ دوران النجم بسبب الكبح، هناك أيضا انخفاض في معدل فقدان الزخم الزاوي.في ظل هذه الظروف، النجوم تقترب تدريجيا، من حالة التوقف عن الدوران لكنها لا تصل ابدا لهذة المرحلة.[24]
أنظمة النجوم الثنائية الوثيقة
النجوم الثنائية هي عبارة عن نجمين يدور كل منهما حول الآخر.بمعدل مسافة تفصلهما يعادل مقدار القيمة الأسية للأقطار النجمين. في هذه المسافات، يمكن أن تحدث تفاعلات كثيرة معقدة، مثل تأثيرات المد والجزر، وتبادل للكتلة وربما الاصطدام. تفاعلات المد والجزر في أنظمة النجوم الثنائية الوثيقة يمكن أن تؤدي إلى تعديل المعلمات المدارية والدورانية للنجوم.ويبقى مجموع الزخم الزاوي للنظام محفوظ، لكن الزخم الزاوي يمكن ان يتنقل بين الفترات المدارية ومعدلات الدوران.[25]
كل عضو من أعضاء النظام الثنائي الوثيق يزيد من تفاعل تاثير المد والجزر على ر على نجم المرافق لة من خلال تفاعل الجاذبية.ومع ذلك، فإن الانتفاخات الناشئة قد لا تكون متوافقة تماما مع اتجاه الجاذبية، وفي هذه الحالة، فإن قوة الجاذبية تمارس عنصر قوة الدفع التي تنطوي على نقل الزخم الزاوي (التسارع المدي). هذا يؤدي إلى التطور المستمر للنظام، على الرغم من أن هذا النهج يمكن أن يقترب من مرحلة توازن مستقر. والتأثير يمكن أن يصبح أكثر تعقيدا في الحالات التي يكون فيها محور الدوران ليس عمودي على المستوى المداري.[25]
في النظام النجمي الثنائي المتصل اوالشبه منفصل نقل الكتلة من النجم المرافق يمكن أن يؤدي أيضا إلى نقل كبير للزخم الزاوي. النجم الرفيق النامي يمكن أن يدورالى ان يصل إلى النقطة التي يكون فيها معدل دورانة حرج ويبدأ بفقدان كتلة على طول خط الاستواء.[26]
النجوم المتهالكة
بعد انتهاء النجم من توليد الطاقة من خلال الاندماج النووي الحراري، يتطور إلى حالة متهالكة أكثر إحكاما. وخلال هذه العملية تتقلص أبعاد النجم بشكل كبير، والذي يمكن أن يؤدي في المقابل إلى زيادة في السرعة الزاوية.
القزم الأبيض
القزم الأبيض هو النجم الذي يتكون من المواد التي هي نتاج الاندماج النووي الحراري خلال الجزء الأول من حياته، لكنه يفتقر إلى الكتلة الازمة لحرق تلك العناصر على نطاق واسع.وهو جرم مدمج يدعمه تأثير الكم الميكانيكي المعروف باسم ضغط الانحطاط الإلكتروني الذي لن يسمح للنجم بأن ينهار أكثر من ذلك . وعموما معظم الأقزام البيضاء لديها معدل دوران منخفض، وعلى الأرجح نتيجة كبح التدوير أو من خلال فقدان الزخم الزاوي عندما يخسر النجم السلف غلافة الخارجي .[27]
القزم الأبيض البطئ الدوران لا يمكن أن يتجاوز حد شاندراسيخار 1.44 كتلة شمسية دون أن ينهار لتشكيل نجم نيوتروني أو ينفجر كمستعر أعظم من النوع الأول (أ).وبمجرد أن يصل القزم الأبيض إلى هذه الكتلة، بسبب التراكم أو التصادم، فإن قوة الجاذبية تتجاوز الضغوط التي تمارسها الإلكترونات إذا كان القزم الأبيض يدور بسرعة، ومع ذلك، تتناقص قوة الجاذبية الفعالة في المنطقة الاستوائية، وبالتالي السماح للقزم الأبيض إلى ان يتجاوز حد شاندراسيخار .ويمكن أن يحدث هذا الدوران السريع، على سبيل المثال، نتيجة لتراكم الكتلة الذي يؤدي إلى نقل الزخم الزاوي.[28]
النجم النيوتروني

النجم النيوتروني هو من بقايا كثيفة للغاية من نجم يتكون أساسا من النيوترونات، الجسيمات التي يتم العثور عليها في معظم النوى الذرية وليس لديها شحنة كهربائية . وتتراوح كتلة النجم النيوتروني في نطاق بين 1.2 و 2.1 مرة كتلة الشمس. ونتيجة لانهيار النجم النيوتروني، يمكن ان يكون لنجم نيوتروني شكل حديثا معدل سرعة دوران عالى جدا. قد يصل إلى مئة دورة في الثانية الواحدة.
النجوم النابضة هي نجوم نيوترونية تدور بسرعة عالية، ولها مجال مغناطيسي قوي. وينبعث شعاع ضيق من الإشعاع الكهرومغناطيسي من أقطاب النجوم النابضة الدوارة.. إذا اتجة الشعاع باتجاة النظام الشمسي سوف ينتج النجم نبض دوري الذي يمكن أن يتم رصدة من الأرض.وتبطئ الطاقة المنبعثة من الحقل المغناطيسي تدريجيا من معدل الدوران، بحيث ان النجوم النابضة الكبيرة في السن تستغرق عدة ثوان بين كل نبضة.[29]
الثقب الأسود
الثقب الأسود هو جرم فلكي لة حقل جاذبية قوي بما فيه الكفاية ليمنع الضوء من الهرب وعندما يتم تشكيلها من انهيار الكتلة الدوارة، فإن الثقوب السوداء تحتفظ بكل الزخم الزاوي الذي لم يهدر على شكل غاز مقذوف.هذا الدوران يتسبب في سحب الفضاء حول الثقب الأسود ضمن مجال على شكل كروي مفلطح، يسمى "ergosphere"، الكتلة الواقعة في هذا المجال تكتسب الطاقة عن طريق هذه العملية ويمكن بعد ذلك إخراج جزء من الكتلة من دون الوقوع في الثقب الأسود.وعندما يتم إخراج الكتلة، يفقد الثقب الأسود الزخم الزاوي وتسمى هذة العملية ("عملية بنروز").[30] وقد تبين أن معدل سرعة دوران الثقب الأسود قد تصل إلى 98.7٪ من سرعة الضوء.[31]
معلومات
- تعتيم الجاذبية، هى ظاهرة فلكية . تشير إلى دوران النجوم بسرعة كبيرة بحيث يكون لها شكل كروي مفلطح واضح
- الكبح المغناطيسي هي نظرية لشرح فقدان الزخم الزاوي للنجم بسبب المواد التى يحصل عليها النجم بفعل المجال المغناطيسي النجمي
- gyrochronology هى طريقة تقدير عمر نجم منخفض الكتلة شبية بالشمس من خلال معرفة فترة دورانه حول نفسة بهامش خطأ يصل إلى 10%".
اقرأ أيضا
- غليزا 229
- غليزا 299
مراجع
- Donati, Jean-François (5 نوفمبر 2003)، "Differential rotation of stars other than the Sun"، Laboratoire d’Astrophysique de Toulouse، مؤرشف من الأصل في 19 يناير 2017.
- "دوران النجوم حول نفسها يكشف اعمارها"، مركز هارفارد سميثونيان للفيزياء الفلكية - جامعة هارفارد، مؤرشف من الأصل في 4 يونيو 2019، اطلع عليه بتاريخ 27-فبراير- 2017.
{{استشهاد ويب}}: تحقق من التاريخ في:|تاريخ الوصول=(مساعدة) - Shajn, G.؛ Struve, O. (1929)، "On the rotation of the stars"، الإشعارات الشهرية للجمعية الفلكية الملكية، 89: 222–239، Bibcode:1929MNRAS..89..222S، doi:10.1093/mnras/89.3.222.
- Gould, Andrew (1997)، "Measuring the Rotation Speed of Giant Stars from Gravitational Microlensing"، Astrophysical Journal، 483 (1): 98–102، arXiv:astro-ph/9611057، Bibcode:1996astro.ph.11057G، doi:10.1086/304244.
- Soon, W.؛ Frick, P.؛ Baliunas, S. (1999)، "On the rotation of the stars"، The Astrophysical Journal، 510 (2): L135–L138، arXiv:astro-ph/9811114، Bibcode:1999ApJ...510L.135S، doi:10.1086/311805.
- Collier Cameron, A.؛ Donati, J.-F. (2002)، "Doin' the twist: secular changes in the surface differential rotation on AB Doradus"، Monthly Notices of the Royal Astronomical Society، 329 (1): L23–L27، arXiv:astro-ph/0111235، Bibcode:2002MNRAS.329L..23C، doi:10.1046/j.1365-8711.2002.05147.x.
- McAlister, H. A.؛ ten Brummelaar, T. A.؛ وآخرون (2005)، "First Results from the CHARA Array. I. An Interferometric and Spectroscopic Study of the Fast Rotator Alpha Leonis (Regulus)"، The Astrophysical Journal، 628 (1): 439–452، arXiv:astro-ph/0501261، Bibcode:2005ApJ...628..439M، doi:10.1086/430730.
- See "Achernar the Flattest star" in ‘Sky & Telescope’ P. 20 ‘Newsnotes’.
- Hardorp, J.؛ Strittmatter, P. A. (8–11 سبتمبر 1969)، "Rotation and Evolution of be Stars"، Proceedings of IAU Colloq. 4، Ohio State University, Columbus, Ohio: Gordon and Breach Science Publishers، ص. 48، Bibcode:1970stro.coll...48H.
- Kitchatinov, L. L.؛ Rüdiger, G. (2004)، "Anti-solar differential rotation"، Astronomische Nachrichten، 325 (6): 496–500، arXiv:astro-ph/0504173، Bibcode:2004AN....325..496K، doi:10.1002/asna.200410297.
- Ruediger, G.؛ von Rekowski, B.؛ Donahue, R. A.؛ Baliunas, S. L. (1998)، "Differential Rotation and Meridional Flow for Fast-rotating Solar-Type Stars"، Astrophysical Journal، 494 (2): 691–699، Bibcode:1998ApJ...494..691R، doi:10.1086/305216.
- Donati, J.-F.؛ Collier Cameron, A. (1997)، "Differential rotation and magnetic polarity patterns on AB Doradus"، Monthly Notices of the Royal Astronomical Society، 291 (1): 1–19، Bibcode:1997MNRAS.291....1D، doi:10.1093/mnras/291.1.1.
- Korab, Holly (25 يونيو 1997)، "NCSA Access: 3D Star Simulation"، National Center for Supercomputing Applications، مؤرشف من الأصل في 23 يوليو 2008.
- Küker, M.؛ Rüdiger, G. (2004)، "Differential rotation on the lower main sequence"، Astronomische Nachrichten، 326 (3): 265–268، arXiv:astro-ph/0504411، Bibcode:2005AN....326..265K، doi:10.1002/asna.200410387.
- McNally, D. (1965)، "The distribution of angular momentum among main sequence stars"، The Observatory، 85: 166–169، Bibcode:1965Obs....85..166M.
- Ferreira, J.؛ Pelletier, G.؛ Appl, S. (2000)، "Reconnection X-winds: spin-down of low-mass protostars"، Monthly Notices of the Royal Astronomical Society، 312 (2): 387–397، Bibcode:2000MNRAS.312..387F، doi:10.1046/j.1365-8711.2000.03215.x.
- Devitt, Terry (31 يناير 2001)، "What Puts The Brakes On Madly Spinning Stars?"، University of Wisconsin-Madison، مؤرشف من الأصل في 09 ديسمبر 2015.
- Peterson, Deane M.؛ وآخرون (2004)، "Resolving the effects of rotation in early type stars"، New Frontiers in Stellar Interferometry, Proceedings of SPIE Volume 5491، Bellingham, Washington, USA: The International Society for Optical Engineering، ص. 65، Bibcode:2004SPIE.5491...65P.
- Tassoul, Jean-Louis (2000)، Stellar Rotation (PDF)، Cambridge, MA: Cambridge University Press، ISBN 0-521-77218-4، مؤرشف من الأصل (PDF) في 9 أكتوبر 2018، اطلع عليه بتاريخ 26 يونيو 2007.
- Skumanich, Andrew P. (1972)، "Time Scales for CA II Emission Decay, Rotational Braking, and Lithium Depletion"، The Astrophysical Journal، 171: 565، Bibcode:1972ApJ...171..565S، doi:10.1086/151310.
- Skumanich, Andrew P.؛ Eddy, J. A. (1981)، Bonnet, R. M.؛ Dupree, A. K. (المحررون)، Aspects of Long-Term Variability in Sun and Stars - In: Solar Phenomena In Stars and Stellar Systems، Hingham, MA: D. Reidel، ص. 349–398.
- ليون ميستل, 1968, MNRAS, 138, 359−391
- Barnes, Sydney A. (2007)، "Ages for illustrative field stars using gyrochronology: viability, limitations and errors"، The Astrophysical Journal، 669 (2): 1167–1189، arXiv:0704.3068، Bibcode:2007ApJ...669.1167B، doi:10.1086/519295.
- Nariai, Kyoji (1969)، "Mass Loss from Coronae and Its Effect upon Stellar Rotation"، Astrophysics and Space Science، 3 (1): 150–159، Bibcode:1969Ap&SS...3..150N، doi:10.1007/BF00649601.
- Hut, P. (1999)، "Tidal evolution in close binary systems"، Astronomy and Astrophysics، 99 (1): 126–140، Bibcode:1981A&A....99..126H.
- Weaver, D.؛ Nicholson, M. (4 ديسمبر 1997)، "One Star's Loss is Another's Gain: Hubble Captures Brief Moment in Life of Lively Duo"، NASA Hubble، مؤرشف من الأصل في 17 أغسطس 2016.
- Willson, L. A.؛ Stalio, R. (1990)، Angular Momentum and Mass Loss for Hot Stars (ط. 1st)، Springer، ص. 315–16، ISBN 0-7923-0881-6.
- Yoon, S.-C.؛ Langer, N. (2004)، "Presupernova evolution of accreting white dwarfs with rotation"، Astronomy and Astrophysics، 419 (2): 623–644، arXiv:astro-ph/0402287، Bibcode:2004A&A...419..623Y، doi:10.1051/0004-6361:20035822.
- Lorimer, D. R. (28 أغسطس 1998)، "Binary and Millisecond Pulsars"، Max-Planck-Gesellschaft، مؤرشف من الأصل في 3 أغسطس 2016، اطلع عليه بتاريخ أكتوبر 2020.
{{استشهاد ويب}}: تحقق من التاريخ في:|تاريخ الوصول=(مساعدة) - Begelman, Mitchell C. (2003)، "Evidence for Black Holes"، Science، 300 (5627): 1898–1903، Bibcode:2003Sci...300.1898B، doi:10.1126/science.1085334، PMID 12817138.
- Tune, Lee (29 مايو 2007)، "Spin of Supermassive Black Holes Measured for First Time"، University of Maryland Newsdesk، مؤرشف من الأصل في 20 يناير 2014، اطلع عليه بتاريخ أكتوبر 2020.
{{استشهاد بخبر}}: تحقق من التاريخ في:|تاريخ الوصول=(مساعدة)
- بوابة علم الفلك
- بوابة نجوم