مبرهنة ستيوارت
في الهندسة الرياضية، تظهر مبرهنة ستيوارت العلاقة بين أطوال أضلاع مثلث وطول القطعة المستقيمة الواصلة بين رأس من رؤوسه والضلع المقابل لهذا الرأس.[1]
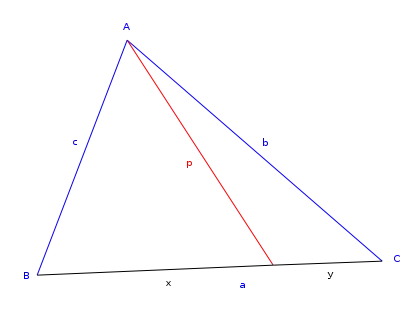
مبرهنة ستيوارت
إذا كانت a, b, c أضلاع مثلث ِABC، وكانت p قطعة مستقيمة من الرأس A إلى نقطة تقسم الضلع a إلى y و x عندها تعطى المبرهنة بالشكل التالي:
البرهان
بتطبيق قانون جيب التمام نجد أن:
و
بضرب المعادلة الأولى بـ x و المعادلة الثانية بـ y ينتج أن:
من خواص دالة الجيب التمام أن:
و لهذا السبب عند جمع المعادلتين سيختفي وسيبقى:
مراجع
- "معلومات عن مبرهنة ستيوارت على موقع mathworld.wolfram.com"، mathworld.wolfram.com، مؤرشف من الأصل في 6 نوفمبر 2019.
- بوابة رياضيات
- بوابة هندسة رياضية
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.