مدار
المدار في الفيزياء هو مسار منحني لجسم ما حول نقطة أو جسم آخر تحت تأثير قوة الجاذبية. على سبيل المثال مدار كوكب حول نجم، مثل دوران كواكب المجموعة الشمسية حول الشمس.[1][2] مدارات الكواكب غالباً ما تكون دائرية أو إهليجية (في شكل القطع الناقص).
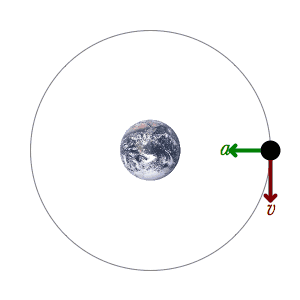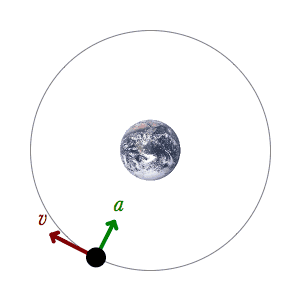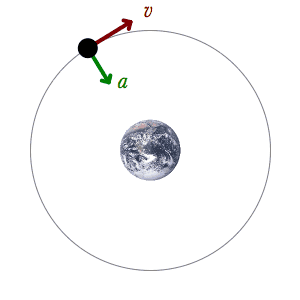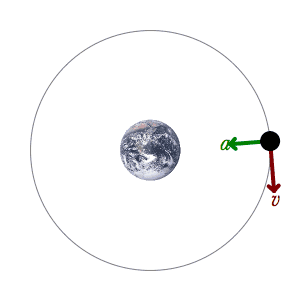
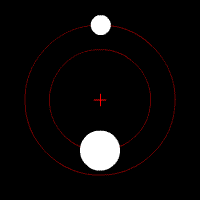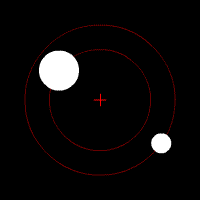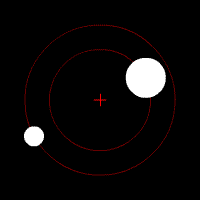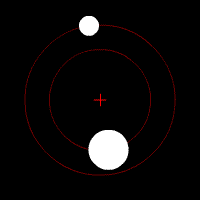
الفهم الحالي للحركة المدارية قائم على نظرية النسبية العامة للعالم ألبرت أينشتاين، والتي تنص على أن الجاذبية هي نتيجة لوجود انحناء في الزمكان، مع اتباع المدارات لقوانين علم الجيوديسيا. ولتسهيل الحسابات، تقرب باستخدام قانون الجذب العام لنيوتن وهو قائم على قوانين حركة الكواكب للعالم كبلر، وتنطبق في حالة حركة الأجسام عند سرعات أقل كثيرا عن سرعة الضوء في الفراغ. [3] أما إذا كانت سرعة الأجسام أو الجسيمات قريبة من سرعة الضوء فلا بد من تطبيق معادلات النظرية النسبية الخاصة لأينشتاين، وإلا حصلنا على نتائج بعيدة عن الحقيقة.
مدار قمر صناعي
تختلف ارتفاعات مدارات الأقمار الصناعية بحسب الغرض منها، ويوجد منها نوعان:
مدار منخفض

معظم مدارات الأقمار الصناعية حول الأرض تكون غالبا قريبة من الأرض على ارتفاع نحو 500 كيلومتر. في هذا المدار يتم القمر الصناعي أو محطة الفضاء الدولية دورة كاملة كل نحو 90 دقيقة. تلك هي الأقمار الصناعية التي تستخدم في الاستشعار عن بعد والتصوير ومسح الأرض، ورصد حالة الطقس.
مدار متوسط
معظم الأقمار الصناعية المتواجدة في هذا المدار تكون على ارتفاع يقارب 20000 كيلومتر. من بين تلك الأقمار التي ترسل إلى هذا الارتفاع الأقمار الصناعية المستخدمة في نظام التموضع العالمي GPS، حيث تقوم بدورة كاملة حول الأرض في 12 ساعة.
المدار الجغرافي الثابت

هذا المدار يكون مدارا عاليا ويسمى المدار الجغرافي الثابت، يبلغ ارتفاعه نحو 35.8 ألف كيلومتر عن الأرض. ميزته أن القمر الصناعي الموجود فيه يظل ثابتا فوق الموقع الجغرافي الذي تحته على الأرض. فهو يتم دورته في هذا المدار خلال 24 ساعة، وهي نفس سرعة دوران الأرض حول محورها.
مدارات كوكبية
توجد داخل مجموعة كوكبية كواكب، وأقزام كواكب، وكويكبات، ومذنبات، يدور كل منها في مدار (يسمى المدار أحيانا فلك). كما تدور نفايات الفضاء أيضا في مدارات. تدور تلك الأجرام حول الشمس، وبالتمام تدور حول ما يسمى مركز الثقل الذي يتحدد بالنسبة بين الجسم الكبير والجسم الصغير ويقع هذا المركز بينهما. شكل المدار يكون في العادة ليس مستديرا تماما وإنما يكون في شكل قطع ناقص. أما المذنبات فقد يكون شكل أفلاكها قطع زائد أو قطع مكافئ وهي تدور حول مركز الثقل بينها وبين الشمس، لأنها ليست مرتبطة ارتباطا جاذبيا مع الشمس، وتعتبر لا تنتمي إلى المجموعة الشمسية. اكتشفت لنجوم أخرى كواكب وربما يكون لها أيضا كويكبات ومذنبات. الأجسام التي ترتبط بالجاذبية بأحد الكواكب قد تكون توابع (أقمار) طبيعية أو أقمارا صناعية، وهي أيضا تدور حول مركز الثقل بينها وبين الكوكب.
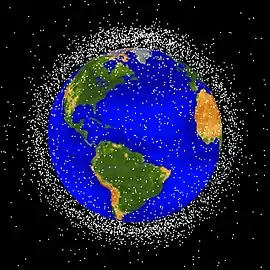
مثال: لدينا في المجموعة الشمسية: تدور الأرض حول مركز الثقل بينها وبين الشمس (يقع مركز الثقل داخل الشمس بسبب الكبر العظيم لكتلة الشمس بالنسبة لكتلة الأرض). ويدور القمر في فلك حول مركز الثقل بينه وبين الأرض. وتدور الأقمار الصناعية ومحطة الفضاء الدولية حول الأرض، كما يوجد الكثير من المخلفات الفضائية التي يسببها النشاط الإنساني في الفضاء، وهي تدور في مدارات منخفضة حول الأرض.
قوانين نيوتن للحركة
في الأحوال عندما تكون تأثيرات النظرية النسبية (في حالة السرعات الأقل بكثير من سرعة الضوء) يمكن إهمالها تعطي قوانين نيوتن وصفا دقيقا لحركة الأجسام. ويكون تسريع كل جسم مساويا لمجموع قوى الجاذبية عليه مقسومة على كتلته. وتكون قوة الجاذبية بين جسمين متناسبة تناسبا طرديا مع حاصل ضرب كتلتيهما، ومتناسبة عكسيا مع مربع لمسافة بينهما. فإذا كانت كتلة أحد الجسمين كبيرة جدا بالنسبة لكتلة الجسم الآخر، مثلما في حالة قمر صناعي مرتبط بالأرض أو حالة الأرض التي تدور حول الشمس، فيمكن حساب حول مركز الجسم الأكبر، ونقول عندئذ أن الجسم الأصغر يدور في مدار حول الجسم الأكبر. أما في حالة أن تكون كتلتي الجسمين متقاربتين، فيمكن أيضا حساب حركتهما بالنسبة لبعضهما البعض بقوانين نيوتن بدقة عن طريق اعتبار أن الجسمين يدوران حول مركز ثقلهما.
يرتبط حقل الجاذبية بطاقة. فيمكن لجسم بعيد عن جسم آخر أن يؤدي شغلا إذا كان منجذبا إليه تحت فعل الجاذبية، ولذلك يكون له طاقة وضع. ونظرا لأنه لا بد من أداء شغل لفصل جسمين عن بعضهما البعض ضد جاذبيتهما تزداد طاقة وضعهما كلما ابتعدا عن بعضهما البعض، وتقل طاقة وضعهما كلما اقتربا من بعضهما. وبالنسبة إلى كتلتين نقطيتين (كل منهما مركزة في نقطة) تزداد طاقة الجاذبية بطريقة لا نهاية عندما تصبح المسافة بينهما صفرا، وبالتالي يمكن اعتبار طاقة الوضع لهما مساوية للصفر عندما تكون المسافة بينهما مقاربة للصفر، وقد تكون سالبة (حيث أنها تقل عن الصفر) عندما تصغر المسافة بينهما إلى أقل من ذلك.
يكون شكل مدار جسم صغير حول جسم كبير في شكل مقطع مخروط. فيمكن أن يكون المدار مفتوحا (أي يبعد الجسم الصغير عن الجسم الكبير ولا يعود)، أو يمكن أن يكون المدار مغلقا (فيكون الجسم الصغير مرتبطا بالكبير) وهذا يعتمد على الطاقة الكلية للنظام (طاقة الحركة + طاقة الوضع). في حالة المدار المفتوح تكون السرعة في المدار عن أي نقطة مساوية على الأقل لسرعة الإفلات فتكون السرعة أقل من سرعة الفرار. ونظرا لكون طاقة الحركة باستمرار موجبة - طبقا للمصطلح عليه حيث تعتبر طاقة الوضع مساوية للصفر في مسافة لا نهائية بين الجسمين - فيكون للمدار المغلق طاقة كلية سالبة، ولفلك في شكل قطع مكافئ تكون الطاقة الكلية مساوية للصفر، وفي حالة القطع الزائد يكون لفلك الجسم طاقة كلية موجبة.
يكون المدار المفتوح في شكل القطع الزائد (عندما تكون السرعة أكبر من سرعة الإفلات)، أو في شكل القطع المكافئ (عندما تكون السرعة مساوية تماما لسرعة الإفلات). يقترب الجسمين من بعضهما البعض وينحني خط سيرهما حول بعضهما عند أقرب نقطة بينهما، ثم يبتعدان عن بعضهما إلى الأبد. وهذا ما يحدث لبعض المذنبات عندما يأتون من خارج المجموعة الشمسية.
يتخذ مدار مغلق شكل قطع ناقص. وفي الحالة الخاصة عندما تكون المسافة بين الجسمين متساوية فيكون المدار دائري، فإذا كان مدار الجسم الذي يدور حول الأرض في شكل قطع الناقص تسمى أقرب نقطة بينهما حضيض، تسمى أبعد نقطة على المدار بينهما أوج. والخط الواصل بين هاتين النقطتين هو المحور الأكبر للقطع الناقص.
تعيد أجسام ذات مدارات مغلقة دورتها حول بعضها خلال فترات زمنية ثابتة (مثل دورة الأرض حول الشمس خلال 25و365 يوم) وهذه الحركة يصفها القانون التجريبي لكيبلر والذي يمكن استنتاجه من قوانين نيوتن. ويمكن صياغة هذا القانون كالآتي:
القانون الأول لكيبلر:
- "يكون مدار كوكب حول الشمس في شكل قطع ناقص بحيث تكون الشمس في أحد مركزي القطع الناقص". ويقع المدار على مستوى يسمى "المستوى المداري".
القانون الثاني لكيبلر":

- "وبينما يدور كوكب في مداره خلال دورة زمنية ثابتة، فيقطع الخط الواصل بينه وبين الشمس مساحات متساوية في المستوى المداري خلال فترة زمنية محددة، بصرف النظر عن موقعه في المدار". وهذا معناه أن الكوكب يتحرك بسرعة أكبر عن اقترابه من اٌقرب نقطة له مع الشمس، وتقل سرعته عند أبعد نقطة عنها. يصاغ هذا القانون أحيانا "مساحات متساوية خلال أزمنة متساوية".
القانون الثالث لكيبلر:
- "بالنسبة إلى مدارات الكواكب، تكون نسبة مكعب نصف المحور الأكبر إلى مربع زمن الدورة مقدار ثابت".
حساب مدار منخفض
عند اعتبار أن المدار دائري الشكل يمكن جعل القوة الوزنية مساوية للقوة المركزية الطاردة، ونحصل على سرعة دوران مثلا الأرض حول الشمس، وزمن الدورة.
حيث:
- = القوة الوزنية،
- = ثابت الجاذبية،
- = كتلة التابع،
- = كتلة الجسم المركزي،
- = نصف قطر الجسم المركزي.
وتعطى القوة الوزنية لقمر صناعي يدور حول الأرض مع استخدام متوسط كثافة الأرض (بدلا من كتلتها) فنحصل على:
وبمساواة هذه المعادلة بمعادلة القوة الوزنية نحصل على التسارع المركزي (في حالة الأرض هو عجلة الجاذبية):
ونفترض أن القوة الوزنية والقوة الطاردة المركزية عند السرعة في المدار متساويتان:
وبحل المعادلة للحصول على السرعة وإجراء الاختصارات لكتلة القمر الصناعي :
نحصل على زمن الدورة
أي أن زمن الدورة = المحيط / السرعة:
وبصرف النظر عن الثوابت الطبيعية يعتمد زمن الدورة على كثافة الجسم المركزي، ولا يعتمد على نصف قطره.
القيــم في حالة الأرض:
يبلغ زمن الدورة 90 دقيقة بالنسبة لمدار منخفض حول الأرض، وهو ينطبق على معظم المركبات الفضائية المأهولة التي تدور حول الأرض.
بغرض المقارنة، فلنعتبر القمر فوبوس:
ورغم أن قطر فوبوس يبلغ 25 كيلومتر فقط، يكون زمن الدورة حوله في مدار منخفض مساويا تقريبا لزمن الدورة على الأرض (وزمن دورته في الحقيقة أكبر). ولكن السرعة في هذا المدار تكون 33 كيلومتر / الساعة. أي أن رائد الفضاء الذي يكون على القمر فوبوس يستطيع قذف كرة تنس بيده إلى مدار فوق فوبوس.
مصادر
- The Space Place :: What's a Barycenter نسخة محفوظة 07 مايو 2011 على موقع واي باك مشين.
- orbit (astronomy) – Britannica Online Encyclopedia نسخة محفوظة 05 مايو 2015 على موقع واي باك مشين.
- Kuhn, The Copernican Revolution, pp. 238, 246–252
اقرأ أيضا
- بوابة نجوم
- بوابة المجموعة الشمسية
- بوابة علوم
- بوابة رياضيات
- بوابة الفيزياء
- بوابة الفضاء
- بوابة علم الفلك
- بوابة رحلات فضائية