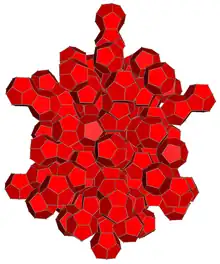
120-cell
In geometry, the 120-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {5,3,3}. It is also called a C120, dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, polydodecahedron, hecatonicosachoron, dodecacontachoron[1] and hecatonicosahedroid.[2]
| 120-cell | |
|---|---|
 Schlegel diagram (vertices and edges) | |
| Type | Convex regular 4-polytope |
| Schläfli symbol | {5,3,3} |
| Coxeter diagram | |
| Cells | 120 {5,3} |
| Faces | 720 {5} |
| Edges | 1200 |
| Vertices | 600 |
| Vertex figure |  tetrahedron |
| Petrie polygon | 30-gon |
| Coxeter group | H4, [3,3,5] |
| Dual | 600-cell |
| Properties | convex, isogonal, isotoxal, isohedral |
| Uniform index | 32 |
The boundary of the 120-cell is composed of 120 dodecahedral cells with 4 meeting at each vertex. Together they form 720 pentagonal faces, 1200 edges, and 600 vertices. It is the 4-dimensional analogue of the regular dodecahedron, since just as a dodecahedron has 12 pentagonal facets, with 3 around each vertex, the dodecaplex has 120 dodecahedral facets, with 3 around each edge.[lower-alpha 1] Its dual polytope is the 600-cell.
Geometry
The 120-cell incorporates the geometries of every convex regular polytope in the first four dimensions (except the polygons {7} and above).[lower-alpha 2] As the sixth and largest regular convex 4-polytope,[lower-alpha 3] it contains inscribed instances of its four predecessors (recursively). It also contains 120 inscribed instances of the first in the sequence, the 5-cell,[lower-alpha 4] which is not found in any of the others.[4] The 120-cell is a four-dimensional Swiss Army knife: it contains one of everything.
It is daunting but instructive to study the 120-cell, because it contains examples of every relationship among all the convex regular polytopes found in the first four dimensions. Conversely, it can only be understood by first understanding each of its predecessors, and the sequence of increasingly complex symmetries they exhibit.[5] That is why Stillwell titled his paper on the 4-polytopes and the history of mathematics[6] of more than 3 dimensions The Story of the 120-cell.[7]
| Regular convex 4-polytopes | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry group | A4 | B4 | F4 | H4 | |||
| Name | 5-cell Hyper-tetrahedron |
16-cell Hyper-octahedron |
8-cell Hyper-cube |
24-cell
|
600-cell Hyper-icosahedron |
120-cell Hyper-dodecahedron | |
| Schläfli symbol | {3, 3, 3} | {3, 3, 4} | {4, 3, 3} | {3, 4, 3} | {3, 3, 5} | {5, 3, 3} | |
| Coxeter mirrors | |||||||
| Mirror dihedrals | 𝝅/3 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/3 𝝅/4 𝝅/2 𝝅/2 𝝅/2 | 𝝅/4 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/4 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/3 𝝅/5 𝝅/2 𝝅/2 𝝅/2 | 𝝅/5 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | |
| Graph |  |
 |
 |
 |
 |
 | |
| Vertices | 5 tetrahedral | 8 octahedral | 16 tetrahedral | 24 cubical | 120 icosahedral | 600 tetrahedral | |
| Edges | 10 triangular | 24 square | 32 triangular | 96 triangular | 720 pentagonal | 1200 triangular | |
| Faces | 10 triangles | 32 triangles | 24 squares | 96 triangles | 1200 triangles | 720 pentagons | |
| Cells | 5 tetrahedra | 16 tetrahedra | 8 cubes | 24 octahedra | 600 tetrahedra | 120 dodecahedra | |
| Tori | 1 5-tetrahedron | 2 8-tetrahedron | 2 4-cube | 4 6-octahedron | 20 30-tetrahedron | 12 10-dodecahedron | |
| Inscribed | 120 in 120-cell | 675 in 120-cell | 2 16-cells | 3 8-cells | 25 24-cells | 10 600-cells | |
| Great polygons | 2 squares x 3 | 4 rectangles x 4 | 4 hexagons x 4 | 12 decagons x 6 | 100 irregular hexagons x 4 | ||
| Petrie polygons | 1 pentagon x 3 | 1 octagon x 3 | 2 octagons x 4 | 2 dodecagons x 4 | 4 30-gons x 6 | 20 30-gons x 4 | |
| Long radius | |||||||
| Edge length | |||||||
| Short radius | |||||||
| Area | |||||||
| Volume | |||||||
| 4-Content | |||||||
Cartesian coordinates
Natural Cartesian coordinates for a 4-polytope centered at the origin of 4-space occur in different frames of reference, depending on the long radius (center-to-vertex) chosen.
√8 radius coordinates
The 120-cell with long radius √8 = 2√2 ≈ 2.828 has edge length 4−2φ = 3−√5 ≈ 0.764.
In this frame of reference, its 600 vertex coordinates are the {permutations} and [even permutations] of the following:[8]
| 24 | ({0, 0, ±2, ±2}) | 24-cell | 600-point 120-cell |
|---|---|---|---|
| 64 | ({±φ, ±φ, ±φ, ±φ−2}) | ||
| 64 | ({±1, ±1, ±1, ±√5}) | ||
| 64 | ({±φ−1, ±φ−1, ±φ−1, ±φ2}) | ||
| 96 | ([0, ±φ−1, ±φ, ±√5]) | Snub 24-cell | |
| 96 | ([0, ±φ−2, ±1, ±φ2]) | Snub 24-cell | |
| 192 | ([±φ−1, ±1, ±φ, ±2]) |
where φ (also called τ) is the golden ratio, 1 + √5/2 ≈ 1.618.
Unit radius coordinates
The unit-radius 120-cell has edge length 1/φ2√2 ≈ 0.270.
In this frame of reference the 120-cell lies vertex up in standard orientation, and its coordinates[9] are the {permutations} and [even permutations] in the left column below:
| 120 | 8 | ({±1, 0, 0, 0}) | 16-cell | 24-cell | 600-cell | 120-cell |
|---|---|---|---|---|---|---|
| 16 | ({±1, ±1, ±1, ±1}) / 2 | Tesseract | ||||
| 96 | ([0, ±φ−1, ±1, ±φ]) / 2 | Snub 24-cell | ||||
| 480 | Diminished 120-cell | 5-point 5-cell | 24-cell | 600-cell | ||
| 32 | ([±φ, ±φ, ±φ, ±φ−2]) / √8 | (1, 0, 0, 0) (−1, √5, √5, √5) / 4 |
({±√1/2, ±√1/2, 0, 0}) | ({±1, 0, 0, 0}) ({±1, ±1, ±1, ±1}) / 2 | ||
| 32 | ([±1, ±1, ±1, ±√5]) / √8 | |||||
| 32 | ([±φ−1, ±φ−1, ±φ−1, ±φ2]) / √8 | |||||
| 96 | ([0, ±φ−1, ±φ, ±√5]) / √8 | |||||
| 96 | ([0, ±φ−2, ±1, ±φ2]) / √8 | |||||
| 192 | ([±φ−1, ±1, ±φ, ±2]) / √8 | |||||
| The unit-radius coordinates of uniform convex 4-polytopes are related by quaternion multiplication. Since the regular 4-polytopes are compounds of each other, their sets of Cartesian 4-coordinates (quaternions) are set products of each other. The unit-radius coordinates of the 600 vertices of the 120-cell (in the left column above) are all the possible quaternion products[10] of the 5 vertices of the 5-cell, the 24 vertices of the 24-cell, and the 120 vertices of the 600-cell (in the other three columns above).[lower-alpha 6] | ||||||
The table gives the coordinates of at least one instance of each 4-polytope, but the 120-cell contains multiples-of-five inscribed instances of each of its precursor 4-polytopes, occupying different subsets of its vertices. The (600-point) 120-cell is the convex hull of 5 disjoint (120-point) 600-cells. Each (120-point) 600-cell is the convex hull of 5 disjoint (24-point) 24-cells, so the 120-cell is the convex hull of 25 disjoint 24-cells. Each 24-cell is the convex hull of 3 disjoint (8-point) 16-cells, so the 120-cell is the convex hull of 75 disjoint 16-cells. Uniquely, the (600-point) 120-cell is the convex hull of 120 disjoint (5-point) 5-cells.[lower-alpha 9]
Chords
The 600-point 120-cell has all 8 of the 120-point 600-cell's distinct chord lengths, plus two additional important chords: its own shorter edges, and the edges of its 120 inscribed regular 5-cells.[lower-alpha 4] These two additional chords give the 120-cell its characteristic isoclinic rotation,[lower-alpha 10] in addition to all the rotations of the other regular 4-polytopes which it inherits.[13] They also give the 120-cell a characteristic great circle polygon: an irregular great hexagon in which three 120-cell edges alternate with three 5-cell edges.[lower-alpha 11]
The 120-cell's edges do not form regular great circle polygons in a single central plane the way the edges of the 600-cell, 24-cell, and 16-cell do. Like the edges of the 5-cell and the 8-cell tesseract, they form zig-zag Petrie polygons instead.[lower-alpha 22] The 120-cell's Petrie polygon is a triacontagon {30} zig-zag skew polygon.[lower-alpha 23]
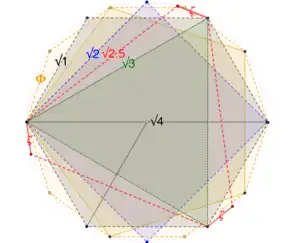
Since the 120-cell has a circumference of 30 edges, it has 15 distinct chord lengths, ranging from its edge length to its diameter.[lower-alpha 27] Every regular convex 4-polytope is inscribed in the 120-cell, and among these 15 chords are all the distinct chords in all the regular 4-polytopes except the 120-cell itself, as enumerated in the 15 rows of the following table.[lower-alpha 13]
The first thing to notice about this table is that it has eight columns, not six: in addition to the six regular convex 4-polytopes, two irregular 4-polytopes occur naturally in the sequence of nested 4-polytopes: the 96-point snub 24-cell and the 480-point diminished 120-cell.[lower-alpha 3]
The second thing to notice is that each numbered row is marked with a triangle △, square ☐, or pentagon ✩. The 15 chords lie in central planes of just three kinds: great square ☐ planes characteristic of the 16-cell, great triangle △ and great hexagon planes characteristic of the 24-cell, or great pentagon ✩ and great decagon planes characteristic of the 600-cell.
| Chords of the 120-cell and its inscribed 4-polytopes[14] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Inscribed[15] | 5-cell | 16-cell | 8-cell | 24-cell | Snub | 600-cell | Dimin | 120-cell | ||||
| Vertices | 5 | 8 | 16 | 24 | 96 | 120 | 480 | 600 | ||||
| Edges | 10[lower-alpha 11] | 24 | 32 | 96 | 432 | 720 | 1200 | 1200[lower-alpha 11] | ||||
| Edge chord | #8[lower-alpha 4] | #7 | #5 | #5 | #3 | #3[lower-alpha 15] | #1 | #1[lower-alpha 15] | ||||
| Isocline chord | #8 | #15 | #10 | #10 | #10 | #5 | #5 | #2 | ||||
| Clifford polygon[lower-alpha 24] | {5/2} | {8/3} | {6/2} | {6/2} | {6/2} | {15/2} | {15/2} | {15/4}[lower-alpha 10] | ||||
| #1 △ |
1/φ2√2 | Petrie 30-gon[lower-alpha 23] | 1 1200[lower-alpha 10] |
4 {3,3} | ||||||||
| 15.5~° | √0.𝜀[lower-alpha 29] | 0.270~ | ||||||||||
| #2 ☐ |
1/φ√2 | face diagonal[lower-alpha 31] | 900 |
| ||||||||
| 25.2~° | √0.19~ | 0.437~ | ||||||||||
| #3 ✩ |
1/φ | great decagon | 10[lower-alpha 9] 720 |
3600 |
24 2{3,5} | |||||||
| 36° | √0.𝚫 | 0.618~ | ||||||||||
| #4 △ |
√3/φ√2 | cell diameter[lower-alpha 12] | 1200 |
4 {3,3} | ||||||||
| 44.5~° | √0.57~ | 0.757~ | ||||||||||
| #5 △ |
great hexagon[lower-alpha 32] | 32 |
225[lower-alpha 9] 96 |
225 |
5[lower-alpha 9] 1200 |
2400 |
8 {4,3} | |||||
| 60° | √1 | 1 | ||||||||||
| #6 ✩ |
√3−φ | great pentagon[lower-alpha 17] | 720 |
3600 |
24 2{3,5} | |||||||
| 72° | √1.𝚫 | 1.175~ | ||||||||||
| #7 ☐ |
great square[lower-alpha 14] | 675[lower-alpha 8] 24 |
675 48 |
72 |
360 |
1800 |
| |||||
| 90° | √2 | 1.414~ | ||||||||||
| #8 △ |
√5/√2 | 5-cell Petrie[lower-alpha 33] | 120[lower-alpha 4] 10 |
720 |
1200[lower-alpha 10] |
4 {3,3} | ||||||
| 104.5~° | √2.5 | 1.581~ | ||||||||||
| #9 ✩ |
φ | golden section | 720 |
3600 |
| |||||||
| 108° | √2.𝚽 | 1.618~ | ||||||||||
| #10 △ |
great triangle | 32 |
25[lower-alpha 9] 96 |
1200 |
2400 |
| ||||||
| 120° | √3 | 1.732~ | ||||||||||
| #11 △ |
{30/11}-gram[lower-alpha 28] | |||||||||||
| 135.5~° | √3.43~ | 1.851~ | ||||||||||
| #12 ✩ |
dihedral | great pent diag | 720 |
3600 |
| |||||||
| 144°[lower-alpha 1] | √3.𝚽 | 1.902~ | ||||||||||
| #13 ☐ |
{30/13}-gram | 900 |
||||||||||
| 154.8~° | √3.81~ | 1.952~ | ||||||||||
| #14 △ |
{30/14}=2{15/7} | |||||||||||
| 164.5~° | √3.93~ | 1.982~ | ||||||||||
| #15 △☐✩ |
𝝅 | diameter | 75[lower-alpha 9] 4 |
8 |
12 |
48 |
60 |
240 |
300[lower-alpha 8] |
1 | ||
| 180° | √4 | 2 | ||||||||||
| Squared total[lower-alpha 34] | 25 | 64 | 256 | 576 | 14400 | 360000[lower-alpha 13] | ||||||
The annotated chord table is a complete bill of materials for constructing the 120-cell. All of the 2-polytopes, 3-polytopes and 4-polytopes in the 120-cell are made from the 15 1-polytopes in the table.
The black integers in table cells are incidence counts of the row's chord in the column's 4-polytope. For example, in the #3 chord row, the 600-cell's 72 great decagons contain 720 #3 chords in all.
The red integers are the number of disjoint 4-polytopes above (the column label) which compounded form a 120-cell. For example, the 120-cell is a compound of 25 disjoint 24-cells (25 * 24 vertices = 600 vertices).
The green integers are the number of distinct 4-polytopes above (the column label) which can be picked out in the 120-cell. For example, the 120-cell contains 225 distinct 24-cells which share components.
The blue integers in the right column are incidence counts of the row's chord at each vertex. For example, in the #3 chord row, 24 #3 chords converge at each of the 120-cell's 600 vertices, forming a double icosahedral vertex figure 2{3,5}.
Relationships among interior polytopes
The 120-cell is the compound of all five of the other regular convex 4-polytopes. All the relationships among the regular 1-, 2-, 3- and 4-polytopes occur in the 120-cell.[lower-alpha 2] It is a four-dimensional jigsaw puzzle in which all those polytopes are the parts.[18] Although there are many sequences in which to construct the 120-cell by putting those parts together, ultimately they only fit together one way. The 120-cell is the unique solution to the combination of all these polytopes.[7]
The regular 1-polytope occurs in only 15 distinct lengths in any of the component regular polytopes of the 120-cell.[lower-alpha 13]
Only 4 of those 15 chords occur in the 16-cell, 8-cell and 24-cell. The four hypercubic chords √1, √2, √3 and √4 are sufficient to build the 24-cell and all its component parts. The 24-cell is the unique solution to the combination of these 4 chords and all the regular polytopes that can be built from them.
An additional 4 of the 15 chords are required to build the 600-cell. The four golden chords are square roots of irrational fractions that are functions of √5. The 600-cell is the unique solution to the combination of these 8 chords and all the regular polytopes that can be built from them. Notable among the new parts found in the 600-cell which do not occur in the 24-cell are pentagons, and icosahedra.
All 15 chords, and 15 other distinct chordal distances not enumerated here, occur in the 120-cell. Notable among the new parts found in the 120-cell which do not occur in the 600-cell are regular 5-cells.[lower-alpha 35] The relationships between the regular 5-cell (the simplex regular 4-polytope) and the other regular 4-polytopes are manifest only in the 120-cell.
Polyhedral graph
Considering the adjacency matrix of the vertices representing the polyhedral graph of the unit-radius 120-cell, the graph diameter is 15, connecting each vertex to its coordinate-negation at a Euclidean distance of 2 away (its circumdiameter), and there are 24 different paths to connect them along the polytope edges. From each vertex, there are 4 vertices at distance 1, 12 at distance 2, 24 at distance 3, 36 at distance 4, 52 at distance 5, 68 at distance 6, 76 at distance 7, 78 at distance 8, 72 at distance 9, 64 at distance 10, 56 at distance 11, 40 at distance 12, 12 at distance 13, 4 at distance 14, and 1 at distance 15. The adjacency matrix has 27 distinct eigenvalues ranging from 1/φ2√2 ≈ 0.270, with a multiplicity of 4, to 2, with a multiplicity of 1. The multiplicity of eigenvalue 0 is 18, and the rank of the adjacency matrix is 582.
The vertices of the 120-cell polyhedral graph are 3-colorable.
The graph is Eulerian having degree 4 in every vertex. Its edge set can be decomposed into two Hamiltonian cycles.[20]
Concentric hulls

Hulls 1, 2, & 7 are each overlapping pairs of Dodecahedrons.
Hull 3 is a pair of Icosidodecahedrons.
Hulls 4 & 5 are each pairs of Truncated icosahedrons.
Hulls 6 & 8 are pairs of Rhombicosidodecahedrons.
Constructions
The 120-cell is the sixth in the sequence of 6 convex regular 4-polytopes (in order of size and complexity).[lower-alpha 3] It can be deconstructed into ten distinct instances (or five disjoint instances) of its predecessor (and dual) the 600-cell,[lower-alpha 7] just as the 600-cell can be deconstructed into twenty-five distinct instances (or five disjoint instances) of its predecessor the 24-cell,[lower-alpha 36] the 24-cell can be deconstructed into three distinct instances of its predecessor the tesseract (8-cell), and the 8-cell can be deconstructed into two disjoint instances of its predecessor (and dual) the 16-cell.[23] The 120-cell contains 675 distinct instances (75 disjoint instances) of the 16-cell.[lower-alpha 8]
The reverse procedure to construct each of these from an instance of its predecessor preserves the radius of the predecessor, but generally produces a successor with a smaller edge length. The 600-cell's edge length is ~0.618 times its radius (the inverse golden ratio), but the 120-cell's edge length is ~0.270 times its radius.
Dual 600-cells

Since the 120-cell is the dual of the 600-cell, it can be constructed from the 600-cell by placing its 600 vertices at the center of volume of each of the 600 tetrahedral cells. From a 600-cell of unit long radius, this results in a 120-cell of slightly smaller long radius (φ2/√8 ≈ 0.926) and edge length of exactly 1/4. Thus the unit edge-length 120-cell (with long radius φ2√2 ≈ 3.702) can be constructed in this manner just inside a 600-cell of long radius 4. The unit radius 120-cell (with edge-length 1/φ2√2 ≈ 0.270) can be constructed in this manner just inside a 600-cell of long radius √8/φ2 ≈ 1.080.
Reciprocally, the unit-radius 120-cell can be constructed just outside a 600-cell of slightly smaller long radius φ2/√8 ≈ 0.926, by placing the center of each dodecahedral cell at one of the 120 600-cell vertices. The 120-cell whose coordinates are given above of long radius √8 = 2√2 ≈ 2.828 and edge-length 2/φ2 = 3−√5 ≈ 0.764 can be constructed in this manner just outside a 600-cell of long radius φ2, which is smaller than √8 in the same ratio of ≈ 0.926; it is in the golden ratio to the edge length of the 600-cell, so that must be φ. The 120-cell of edge-length 2 and long radius φ2√8 ≈ 7.405 given by Coxeter[3] can be constructed in this manner just outside a 600-cell of long radius φ4 and edge-length φ3.
Therefore, the unit-radius 120-cell can be constructed from its predecessor the unit-radius 600-cell in three reciprocation steps.
Cell rotations of inscribed duals
Since the 120-cell contains inscribed 600-cells, it contains its own dual of the same radius. The 120-cell contains five disjoint 600-cells (ten overlapping inscribed 600-cells of which we can pick out five disjoint 600-cells in two different ways), so it can be seen as a compound of five of its own dual (in two ways).[lower-alpha 7] The vertices of each inscribed 600-cell are vertices of the 120-cell, and (dually) each dodecahedral cell center is a tetrahedral cell center in each of the inscribed 600-cells.
The dodecahedral cells of the 120-cell have tetrahedral cells of the 600-cells inscribed in them.[26] Just as the 120-cell is a compound of five 600-cells (in two ways), the dodecahedron is a compound of five regular tetrahedra (in two ways). As two opposing tetrahedra can be inscribed in a cube, and five cubes can be inscribed in a dodecahedron, ten tetrahedra in five cubes can be inscribed in a dodecahedron: two opposing sets of five, with each set covering all 20 vertices and each vertex in two tetrahedra (one from each set, but not the opposing pair of a cube obviously).[27] This shows that the 120-cell contains, among its many interior features, 120 compounds of ten tetrahedra, each of which is dimensionally analogous to the whole 120-cell as a compound of ten 600-cells.
All ten tetrahedra can be generated by two chiral five-click rotations of any one tetrahedron. In each dodecahedral cell, one tetrahedral cell comes from each of the ten 600-cells inscribed in the 120-cell.[lower-alpha 37] Therefore the whole 120-cell, with all ten inscribed 600-cells, can be generated from just one 600-cell by rotating its cells.
Augmentation
Another consequence of the 120-cell containing inscribed 600-cells is that it is possible to construct it by placing 4-pyramids of some kind on the cells of the 600-cell. These tetrahedral pyramids must be quite irregular in this case (with the apex blunted into four 'apexes'), but we can discern their shape in the way a tetrahedron lies inscribed in a dodecahedron.[lower-alpha 38]
Only 120 tetrahedral cells of each 600-cell can be inscribed in the 120-cell's dodecahedra; its other 480 tetrahedra span dodecahedral cells. Each dodecahedron-inscribed tetrahedron is the center cell of a cluster of five tetrahedra, with the four others face-bonded around it lying only partially within the dodecahedron. The central tetrahedron is edge-bonded to an additional 12 tetrahedral cells, also lying only partially within the dodecahedron.[lower-alpha 39] The central cell is vertex-bonded to 40 other tetrahedral cells which lie entirely outside the dodecahedron.
Weyl orbits
Another construction method uses quaternions and the Icosahedral symmetry of Weyl group orbits of order 120.[28] The following describe and 24-cells as quaternion orbit weights of D4 under the Weyl group W(D4):
O(0100) : T = {±1,±e1,±e2,±e3,(±1±e1±e2±e3)/2}
O(1000) : V1
O(0010) : V2
O(0001) : V3
With quaternions where is the conjugate of and and , then the Coxeter group is the symmetry group of the 600-cell and the 120-cell of order 14400.
Given such that and as an exchange of within , we can construct:
- the snub 24-cell
- the 600-cell
- the 120-cell
- the alternate snub 24-cell
- the dual snub 24-cell = .
As a configuration
This configuration matrix represents the 120-cell. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole 120-cell. The nondiagonal numbers say how many of the column's element occur in or at the row's element.[29][30]
Here is the configuration expanded with k-face elements and k-figures. The diagonal element counts are the ratio of the full Coxeter group order, 14400, divided by the order of the subgroup with mirror removal.
| H4 | k-face | fk | f0 | f1 | f2 | f3 | k-fig | Notes | |
|---|---|---|---|---|---|---|---|---|---|
| A3 | ( ) | f0 | 600 | 4 | 6 | 4 | {3,3} | H4/A3 = 14400/24 = 600 | |
| A1A2 | { } | f1 | 2 | 1200 | 3 | 3 | {3} | H4/A2A1 = 14400/6/2 = 1200 | |
| H2A1 | {5} | f2 | 5 | 5 | 720 | 2 | { } | H4/H2A1 = 14400/10/2 = 720 | |
| H3 | {5,3} | f3 | 20 | 30 | 12 | 120 | ( ) | H4/H3 = 14400/120 = 120 |
Visualization
The 120-cell consists of 120 dodecahedral cells. For visualization purposes, it is convenient that the dodecahedron has opposing parallel faces (a trait it shares with the cells of the tesseract and the 24-cell). One can stack dodecahedrons face to face in a straight line bent in the 4th direction into a great circle with a circumference of 10 cells. Starting from this initial ten cell construct there are two common visualizations one can use: a layered stereographic projection, and a structure of intertwining rings.[31]
Layered stereographic projection
The cell locations lend themselves to a hyperspherical description.[32] Pick an arbitrary dodecahedron and label it the "north pole". Twelve great circle meridians (four cells long) radiate out in 3 dimensions, converging at the fifth "south pole" cell. This skeleton accounts for 50 of the 120 cells (2 + 4 × 12).
Starting at the North Pole, we can build up the 120-cell in 9 latitudinal layers, with allusions to terrestrial 2-sphere topography in the table below. With the exception of the poles, the centroids of the cells of each layer lie on a separate 2-sphere, with the equatorial centroids lying on a great 2-sphere. The centroids of the 30 equatorial cells form the vertices of an icosidodecahedron, with the meridians (as described above) passing through the center of each pentagonal face. The cells labeled "interstitial" in the following table do not fall on meridian great circles.
| Layer # | Number of Cells | Description | Colatitude | Region |
|---|---|---|---|---|
| 1 | 1 cell | North Pole | 0° | Northern Hemisphere |
| 2 | 12 cells | First layer of meridional cells / "Arctic Circle" | 36° | |
| 3 | 20 cells | Non-meridian / interstitial | 60° | |
| 4 | 12 cells | Second layer of meridional cells / "Tropic of Cancer" | 72° | |
| 5 | 30 cells | Non-meridian / interstitial | 90° | Equator |
| 6 | 12 cells | Third layer of meridional cells / "Tropic of Capricorn" | 108° | Southern Hemisphere |
| 7 | 20 cells | Non-meridian / interstitial | 120° | |
| 8 | 12 cells | Fourth layer of meridional cells / "Antarctic Circle" | 144° | |
| 9 | 1 cell | South Pole | 180° | |
| Total | 120 cells | |||
The cells of layers 2, 4, 6 and 8 are located over the faces of the pole cell. The cells of layers 3 and 7 are located directly over the vertices of the pole cell. The cells of layer 5 are located over the edges of the pole cell.
Intertwining rings
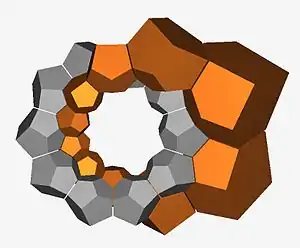
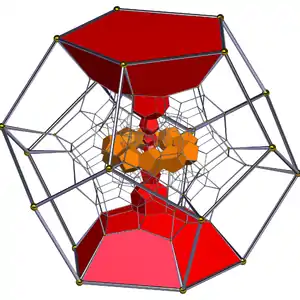
The 120-cell can be partitioned into 12 disjoint 10-cell great circle rings, forming a discrete/quantized Hopf fibration.[33][34][35][36][31] Starting with one 10-cell ring, one can place another ring alongside it that spirals around the original ring one complete revolution in ten cells. Five such 10-cell rings can be placed adjacent to the original 10-cell ring. Although the outer rings "spiral" around the inner ring (and each other), they actually have no helical torsion. They are all equivalent. The spiraling is a result of the 3-sphere curvature. The inner ring and the five outer rings now form a six ring, 60-cell solid torus. One can continue adding 10-cell rings adjacent to the previous ones, but it's more instructive to construct a second torus, disjoint from the one above, from the remaining 60 cells, that interlocks with the first. The 120-cell, like the 3-sphere, is the union of these two (Clifford) tori. If the center ring of the first torus is a meridian great circle as defined above, the center ring of the second torus is the equatorial great circle that is centered on the meridian circle.[37] Also note that the spiraling shell of 50 cells around a center ring can be either left handed or right handed. It's just a matter of partitioning the cells in the shell differently, i.e. picking another set of disjoint (Clifford parallel) great circles.
Other great circle constructs
There is another great circle path of interest that alternately passes through opposing cell vertices, then along an edge. This path consists of 6 edges alternating with 6 cell diameter chords, forming an irregular dodecagon in a central plane.[lower-alpha 12] Both these great circle paths have dual great circle paths in the 600-cell. The 10 cell face to face path above maps to a 10 vertex path solely traversing along edges in the 600-cell, forming a decagon. The alternating cell/edge path maps to a path consisting of 12 tetrahedrons alternately meeting face to face then vertex to vertex (six triangular bipyramids) in the 600-cell. This latter path corresponds to a ring of six icosahedra meeting face to face in the snub 24-cell (or icosahedral pyramids in the 600-cell), and to a great hexagon or a ring of six octahedra meeting face to face in the 24-cell.[lower-alpha 32]
Another great circle polygon path exists which is unique to the 120-cell and has no dual counterpart in the 600-cell. This path consists of 3 120-cell edges alternating with 3 inscribed 5-cell edges (#8 chords), forming the irregular great hexagon with alternating short and long edges illustrated above.[lower-alpha 11] Each 5-cell edge runs through the volume of three dodecahedral cells (in a ring of ten face-bonded dodecahedral cells), to the opposite pentagonal face of the third dodecahedron. This irregular great hexagon lies in the same central plane (on the same great circle) as the irregular great dodecagon described above, but it intersects only {6} of the {12} dodecagon vertices. There are two irregular great hexagons inscribed in each irregular great dodecagon, in alternate positions.[lower-alpha 12]
Perspective projections
| Projections to 3D of a 4D 120-cell performing a simple rotation | |
|---|---|
 |
 |
| From outside the 3-sphere in 4-space. | Inside the 3D surface of the 3-sphere. |
As in all the illustrations in this article, only the edges of the 120-cell appear in these renderings. All the other chords are not shown. The complex interior parts of the 120-cell, all its inscribed 600-cells, 24-cells, 8-cells, 16-cells and 5-cells, are completely invisible in all illustrations. The viewer must imagine them.
These projections use perspective projection, from a specific viewpoint in four dimensions, projecting the model as a 3D shadow. Therefore, faces and cells that look larger are merely closer to the 4D viewpoint.
A comparison of perspective projections of the 3D dodecahedron to 2D (below left), and projections of the 4D 120-cell to 3D (below right), demonstrates two related perspective projection methods, by dimensional analogy. Schlegel diagrams use perspective to show depth in the dimension which has been flattened, choosing a view point above a specific cell, thus making that cell the envelope of the model, with other cells appearing smaller inside it. Stereographic projections use the same approach, but are shown with curved edges, representing the spherical polytope as a tiling of a 3-sphere. Both these methods distort the object, because the cells are not actually nested inside each other (they meet face-to-face), and they are all the same size. Other perspective projection methods exist, such as the rotating animations above, which do not exhibit this particular kind of distortion, but rather some other kind of distortion (as all projections must).
| Projection | Dodecahedron | 120-cell |
|---|---|---|
| Schlegel diagram | 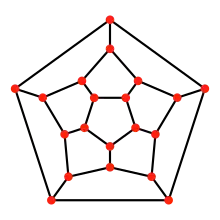 12 pentagon faces in the plane |
 120 dodecahedral cells in 3-space |
| Stereographic projection |  |
 With transparent faces |
| Enhanced perspective projections | |
|---|---|
 |
Cell-first perspective projection at 5 times the distance from the center to a vertex, with these enhancements applied:
|
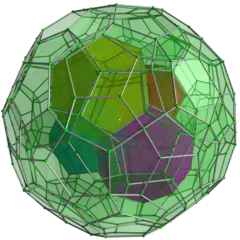 |
Vertex-first perspective projection at 5 times the distance from center to a vertex, with these enhancements:
|
Orthogonal projections
Orthogonal projections of the 120-cell can be done in 2D by defining two orthonormal basis vectors for a specific view direction. The 30-gonal projection was made in 1963 by B. L. Chilton.[39]
The H3 decagonal projection shows the plane of the van Oss polygon.
| H4 | - | F4 |
|---|---|---|
 [30] (Red=1) |
 [20] (Red=1) |
 [12] (Red=1) |
| H3 | A2 / B3 / D4 | A3 / B2 |
 [10] (Red=5, orange=10) |
 [6] (Red=1, orange=3, yellow=6, lime=9, green=12) |
 [4] (Red=1, orange=2, yellow=4, lime=6, green=8) |
3-dimensional orthogonal projections can also be made with three orthonormal basis vectors, and displayed as a 3d model, and then projecting a certain perspective in 3D for a 2d image.
 3D isometric projection |
Animated 4D rotation |
Related polyhedra and honeycombs
H4 polytopes
The 120-cell is one of 15 regular and uniform polytopes with the same H4 symmetry [3,3,5]:[41]
| H4 family polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
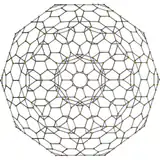
| 120-cell | rectified 120-cell |
truncated 120-cell |
cantellated 120-cell |
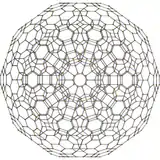
runcinated 120-cell |
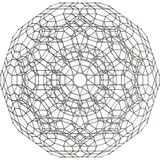
cantitruncated 120-cell |
runcitruncated 120-cell |
omnitruncated 120-cell | ||||
| {5,3,3} | r{5,3,3} | t{5,3,3} | rr{5,3,3} | t0,3{5,3,3} | tr{5,3,3} | t0,1,3{5,3,3} | t0,1,2,3{5,3,3} | ||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
 |
 |
 |
 |
 |
 |
 | |||||
| 600-cell | rectified 600-cell |
truncated 600-cell |
cantellated 600-cell |
bitruncated 600-cell |
cantitruncated 600-cell |
runcitruncated 600-cell |
omnitruncated 600-cell | ||||
| {3,3,5} | r{3,3,5} | t{3,3,5} | rr{3,3,5} | 2t{3,3,5} | tr{3,3,5} | t0,1,3{3,3,5} | t0,1,2,3{3,3,5} | ||||
{p,3,3} polytopes
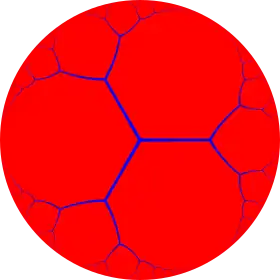
The 120-cell is similar to three regular 4-polytopes: the 5-cell {3,3,3} and tesseract {4,3,3} of Euclidean 4-space, and the hexagonal tiling honeycomb {6,3,3} of hyperbolic space. All of these have a tetrahedral vertex figure {3,3}:
| {p,3,3} polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | S3 | H3 | |||||||||
| Form | Finite | Paracompact | Noncompact | ||||||||
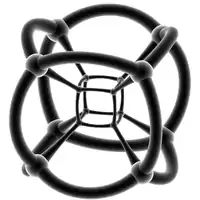
| Name | {3,3,3} | {4,3,3} | {5,3,3} | {6,3,3} | {7,3,3} | {8,3,3} | ...{∞,3,3} | ||||
| Image |  |
 |
 |
 |
 |
 |
 | ||||
| Cells {p,3} |
 {3,3} |
 {4,3} |
 {5,3} |
 {6,3} |
 {7,3} |
 {8,3} |
 {∞,3} | ||||
{5,3,p} polytopes
The 120-cell is a part of a sequence of 4-polytopes and honeycombs with dodecahedral cells:
| {5,3,p} polytopes | |||||||
|---|---|---|---|---|---|---|---|
| Space | S3 | H3 | |||||
| Form | Finite | Compact | Paracompact | Noncompact | |||
| Name | {5,3,3} | {5,3,4} | {5,3,5} | {5,3,6} | {5,3,7} | {5,3,8} | ... {5,3,∞} |
| Image |  |
 |
 |
 |
 |
 |
 |
| Vertex figure |
{3,3} |
{3,4} |
{3,5} |
{3,6} |
{3,7} |
{3,8} |
{3,∞} |
Tetrahedrally diminished 120-cell
Since the 600-point 120-cell has 5 disjoint inscribed 600-cells, it can be diminished by the removal of one of those 120-point 600-cells, creating an irregular 480-point 4-polytope.[lower-alpha 41]

Each dodecahedral cell of the 120-cell is diminished by removal of 4 of its 20 vertices, creating an irregular 16-point polyhedron called the tetrahedrally diminished dodecahedron because the 4 vertices removed formed a tetrahedron inscribed in the dodecahedron. Since the vertex figure of the dodecahedron is the triangle, each truncated vertex is replaced by a triangle. The 12 pentagon faces are replaced by 12 trapezoids, as one vertex of each pentagon is removed and two of its edges are replaced by the pentagon's diagonal chord. The tetrahedrally diminished dodecahedron has 16 vertices and 16 faces: 12 trapezoid faces and four equilateral triangle faces.
Since the vertex figure of the 120-cell is the tetrahedron,[lower-alpha 38] each truncated vertex is replaced by a tetrahedron, leaving 120 tetrahedrally diminished dodecahedron cells and 120 regular tetrahedron cells. The regular dodecahedron and the tetrahedrally diminished dodecahedron both have 30 edges, and the regular 120-cell and the tetrahedrally diminished 120-cell both have 1200 edges.
The 480-point diminished 120-cell may be called the tetrahedrally diminished 120-cell because its cells are tetrahedrally diminished, or the 600-cell diminished 120-cell because the vertices removed formed a 600-cell inscribed in the 120-cell, or even the regular 5-cells diminished 120-cell because removing the 120 vertices removes one vertex from each of the 120 inscribed regular 5-cells, leaving 120 regular tetrahedra.[lower-alpha 4]
Davis 120-cell
The Davis 120-cell, introduced by Davis (1985), is a compact 4-dimensional hyperbolic manifold obtained by identifying opposite faces of the 120-cell, whose universal cover gives the regular honeycomb {5,3,3,5} of 4-dimensional hyperbolic space.
See also
- Uniform 4-polytope family with [5,3,3] symmetry
- 57-cell – an abstract regular 4-polytope constructed from 57 hemi-dodecahedra.
- 600-cell - the dual 4-polytope to the 120-cell
Notes
- In the 120-cell, 3 dodecahedra and 3 pentagons meet at every edge. 4 dodecahedra, 6 pentagons, and 4 edges meet at every vertex. The dihedral angle (between dodecahedral hyperplanes) is 144°.[3]
- The 120-cell contains instances of all of the regular convex 1-polytopes, 2-polytopes, 3-polytopes and 4-polytopes, except for the regular polygons {7} and above, most of which do not occur. {10} is a notable exception which does occur. Various regular skew polygons {7} and above occur in the 120-cell, notably {7}, {11},[lower-alpha 28] {15}[lower-alpha 10] and {30}.[lower-alpha 15]
- The convex regular 4-polytopes can be ordered by size as a measure of 4-dimensional content (hypervolume) for the same radius. Each greater polytope in the sequence is rounder than its predecessor, enclosing more 4-content within the same radius. The 4-simplex (5-cell) is the limit smallest case, and the 120-cell is the largest. Complexity (as measured by comparing configuration matrices or simply the number of vertices) follows the same ordering. This provides an alternative numerical naming scheme for regular polytopes in which the 120-cell is the 600-point 4-polytope: sixth and last in the ascending sequence that begins with the 5-point 4-polytope.
- Inscribed in the unit-radius 120-cell are 120 disjoint regular 5-cells,[11] of edge-length √2.5. No regular 4-polytopes except the 5-cell and the 120-cell contain √2.5 chords (the #8 chord).[lower-alpha 5] The 120-cell contains 10 distinct inscribed 600-cells which can be taken as 5 disjoint 600-cells two different ways. Each √2.5 chord connects two vertices in disjoint 600-cells, and hence in disjoint 24-cells, 8-cells, and 16-cells. These chords and the 120-cell edges occur only in the 120-cell, connecting two vertices in disjoint 600-cells.[lower-alpha 18] Corresponding polytopes of the same kind in disjoint 600-cells are Clifford parallel and √2.5 apart. Each 5-cell contains one vertex from each of 5 disjoint 600-cells (three different ways). Each 5-cell contains three distinct Petrie pentagons of its 5 vertices, pentagonal circuits each binding 5 disjoint 600-cells together in a distinct isoclinic rotation characteristic of the 5-cell.
.svg.png.webp) In triacontagram {30/12}=6{5/2},
In triacontagram {30/12}=6{5/2},
six of the 120 disjoint regular 5-cells of edge-length √2.5 which are inscribed in the 120-cell appear as six pentagrams, the Clifford polygon of the 5-cell. The 30 vertices comprise a Petrie polygon of the 120-cell,[lower-alpha 15] with 30 zig-zag edges (not shown), and 3 inscribed great decagons (edges not shown) which lie Clifford parallel to the projection plane.[lower-alpha 17] - Multiple instances of each of the regular convex 4-polytopes can be inscribed in any of their larger successor 4-polytopes, except for the smallest, the regular 5-cell, which occurs inscribed only in the largest, the 120-cell. To understand the way in which the 4-polytopes nest within each other, it is necessary to carefully distinguish disjoint multiple instances from merely distinct multiple instances of inscribed 4-polytopes. For example, the 600-point 120-cell is the convex hull of a compound of 75 8-point 16-cells that are completely disjoint: they share no vertices, and 75 * 8 = 600. But it is also possible to pick out 675 distinct 16-cells within the 120-cell, most pairs of which share some vertices, because two concentric equal-radius 16-cells may be rotated with respect to each other such that they share 2 vertices (an axis), or even 4 vertices (a great square plane), while their remaining vertices are not coincident.[lower-alpha 8] In 4-space, any two congruent regular 4-polytopes may be concentric but rotated with respect to each other such that they share only a common subset of their vertices. Only in the case of the 4-simplex (the 5-point regular 5-cell) that common subset of vertices must always be empty, unless it is all 5 vertices. It is impossible to rotate two concentric 4-simplexes with respect to each other such that some, but not all, of their vertices are coincident: they may only be completely coincident, or completely disjoint. Only the 4-simplex has this property; the 16-cell, and by extension any larger regular 4-polytope, may lie rotated with respect to itself such that the pair shares some, but not all, of their vertices. Intuitively we may see how this follows from the fact that only the 4-simplex does not possess any opposing vertices (any 2-vertex central axes) which might be invariant after a rotation. The 120-cell contains 120 completely disjoint regular 5-cells, which are its only distinct inscribed regular 5-cells, but every other nesting of regular 4-polytopes features some number of disjoint inscribed 4-polytopes and a larger number of distinct inscribed 4-polytopes.
- To obtain all 600 coordinates by quaternion cross-multiplication of these three 4-polytopes' coordinates with less redundancy, it is sufficient to include just one vertex of the 24-cell: (√1/2, √1/2, 0, 0).[9]
- The vertices of the 120-cell can be partitioned into those of five disjoint 600-cells in two different ways.[25]
- The 120-cell has 600 vertices distributed symmetrically on the surface of a 3-sphere in four-dimensional Euclidean space. The vertices come in antipodal pairs, and the lines through antipodal pairs of vertices define the 300 rays [or axes] of the 120-cell. We will term any set of four mutually orthogonal rays (or directions) a basis. The 300 rays form 675 bases, with each ray occurring in 9 bases and being orthogonal to its 27 distinct companions in these bases and to no other rays. The rays and bases constitute a geometric configuration, which in the language of configurations is written as 30096754 to indicate that each ray belongs to 9 bases, and each basis contains 4 rays.[24] Each basis corresponds to a distinct 16-cell containing four orthogonal axes and six orthogonal great squares. 75 completely disjoint 16-cells containing all 600 vertices of the 120-cell can be selected from the 675 distinct 16-cells.[lower-alpha 5]
- The 120-cell can be constructed as a compound of 5 disjoint 600-cells,[lower-alpha 7] or 25 disjoint 24-cells, or 75 disjoint 16-cells, or 120 disjoint 5-cells. Except in the case of the 120 5-cells,[lower-alpha 5] these are not counts of all the distinct regular 4-polytopes which can be found inscribed in the 120-cell, only the counts of completely disjoint inscribed 4-polytopes which when compounded form the convex hull of the 120-cell. The 120-cell contains 10 distinct 600-cells, 225 distinct 24-cells, and 675 distinct 16-cells.[lower-alpha 8]
- The characteristic isoclinic[lower-alpha 21] rotation of the 120-cell takes place in the invariant planes of its 1200 edges[lower-alpha 22] and its inscribed regular 5-cells' 1200 edges.[lower-alpha 11] There are four distinct characteristic right (and left) isoclinic rotations, each left-right pair corresponding to a discrete Hopf fibration.[12] In each rotation all 600 vertices circulate on helical isoclines of 15 vertices, following a geodesic circle with 15 #2 chords that form a {15/4} pentadecagram.[lower-alpha 20]
.svg.png.webp) In triacontagram {30/8}=2{15/4},
In triacontagram {30/8}=2{15/4},
2 disjoint pentadecagram isoclines are visible: a black and a white isocline (shown here as orange and faint yellow) of the 120-cell's characteristic isoclinic rotation.[lower-alpha 19] The pentadecagram edges are #2 chords joining vertices which are 8 vertices apart on the 30-vertex circumference of this projection, but only 2 zig-zag edges apart in the completely orthogonal projection on a Petrie polygon.[lower-alpha 20] - The invariant central plane of the 120-cell's characteristic isoclinic rotation[lower-alpha 10] contains an irregular great hexagon {6} with alternating edges of two different lengths: 3 120-cell edges of length 𝜁 = √0.𝜀 (#1 chords), and 3 inscribed regular 5-cell edges of length √2.5 (#8 chords). These are, respectively, the shortest and longest edges of any regular 4-polytope. Each √2.5 chord is spanned by 9 zig-zag edges of a Petrie 30-gon.[lower-alpha 23] Each irregular great hexagon lies completely orthogonal to another irregular great hexagon. The 120-cell contains 400 distinct irregular great hexagons (200 completely orthogonal pairs), which can be partitioned into 100 disjoint irregular great hexagons (a discrete fibration of the 120-cell) in four different ways. Each fibration has its distinct left (and right) isoclinic rotation in 50 pairs of completely orthogonal invariant central planes. Two irregular great hexagons occupy the same central plane, in alternate positions, just as two great pentagons occupy a great decagon plane. The two irregular great hexagons form an irregular great dodecagon, a compound great circle polygon of the 120-cell which is illustrated separately.[lower-alpha 12]
- The 120-cell has an irregular dodecagon {12} great circle polygon of 6 edges (#1 chords marked 𝜁) alternating with 6 dodecahedron cell-diameters (#4 chords).[lower-alpha 30] The irregular great dodecagon contains two irregular great hexagons (red) inscribed in alternate positions.[lower-alpha 11] Two regular great hexagons with edges of a third size (√1, the #5 chord) are also inscribed in the dodecagon.[lower-alpha 32] The twelve regular hexagon edges (#5 chords), the six cell-diameter edges of the dodecagon (#4 chords), and the six 120-cell edges of the dodecagon (#1 chords), are all chords of the same great circle, but the other 24 zig-zag edges (#1 chords, not shown) that bridge the six #4 edges of the dodecagon do not lie in this great circle plane. The 120-cell's irregular great dodecagon planes, its irregular great hexagon planes, its regular great hexagon planes, and its equilateral great triangle planes, are the same set of dodecagon planes. The 120-cell contains 200 such {12} central planes (100 completely orthogonal pairs), the same 200 central planes each containing a hexagon that are found in each of the 10 inscribed 600-cells.[lower-alpha 40]
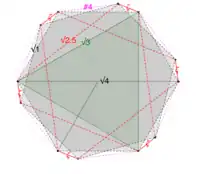 The 120-cell has 200 central planes that each intersect 12 vertices, forming an irregular dodecagon with alternating edges of two different lengths. Inscribed in the dodecagon are two regular great hexagons (black),[lower-alpha 32] two irregular great hexagons (red),[lower-alpha 11] and four equilateral great triangles (only one is shown, in green).
The 120-cell has 200 central planes that each intersect 12 vertices, forming an irregular dodecagon with alternating edges of two different lengths. Inscribed in the dodecagon are two regular great hexagons (black),[lower-alpha 32] two irregular great hexagons (red),[lower-alpha 11] and four equilateral great triangles (only one is shown, in green). - The 120-cell itself contains more chords than the 15 in the table, but those additional chords occur only in the 120-cell, not in any of its components (the other five regular convex 4-polytopes). There are 30 distinct nonzero 4-space chordal distances between vertices of the 120-cell.
- The 120-cell contains 450 great square polygons.[lower-alpha 8] They lie in pairs in 225 central planes. Two great squares in the same central plane belong to completely disjoint 600-cells. Each central plane intersects 8 vertices in an irregular octagon with edges of two different lengths. Four #2 25.2~° chords alternate with four 64.8~° chords (not listed in the table of 15 numbered chords)[lower-alpha 13] to form the octagon. Eight #7 90° √2 chords form the two inscribed great squares. Four #13 154.8~° chords occur as diagonals of the octagon.
 The 120-cell contains an irregular octagon great circle polygon that is a compound of two great square polygons offset from each other by 25.2~°, the arc of the #2 chord.
The 120-cell contains an irregular octagon great circle polygon that is a compound of two great square polygons offset from each other by 25.2~°, the arc of the #2 chord. - The 120-cell and 600-cell both have 30-gon Petrie polygons.[lower-alpha 25] They are two different skew 30-gon helices, composed of 30 120-cell edges (#1 chords) and 30 600-cell edges (#3 chords) respectively, but they occur in pairs that spiral around the same 0-gon great circle axis. The 120-cell's Petrie helix winds closer to the axis than the 600-cell's Petrie helix does, because its 30 edges are shorter than the 600-cell's 30 edges (and they zig-zag at less acute angles). A pair of these two helices of different radii sharing an axis do not have any vertices in common; they are completely disjoint. Both helices twist around the 0-gon axis many times in the course of one circular orbit, forming a {30/8} polygram[lower-alpha 23] or a {30/11} polygram[lower-alpha 28] respectively.
- In 600-cell § Decagons and pentadecagrams, see the illustration of triacontagram {30/6}=6{5}.
- Inscribed in the 3 Clifford parallel great decagons of each 30-tetrahedron helical Petrie polygon are 6 great pentagons[lower-alpha 16] in which the 6 pentagrams (regular 5-cells) appear to be inscribed, but the pentagrams are skew (not parallel to the projection plane); each 5-cell actually has vertices in 5 different decagon-pentagon central planes in 5 completely disjoint 600-cells.
- The 120 regular 5-cells are completely disjoint. Each 5-cell contains three distinct Petrie pentagons of its 5 vertices, pentagonal circuits each binding 5 disjoint 600-cells together. But the vertices of two disjoint 5-cells are not linked by 5-cell edges, so each pentagram isocline of 5 #8 chords is confined to a single 5-cell, and there are no other circuits of 5-cell edges (#8 chords) in the 120-cell.
- Each black or white pentadecagram isocline acts as both a right isocline in a distinct right isoclinic rotation and as a left isocline in a distinct left isoclinic rotation, but no isocline is both a right and left isocline of the same distinct left-right rotation (the same fibration).
- The characteristic isocline of the 120-cell is a skew pentadecagram of 15 #2 chords. Successive #2 chords of each pentadecagram lie in different central planes which are inclined isoclinically to each other at 15.5~°, the arc of a 120-cell edge.[lower-alpha 21] Successive vertices of each pentadecagram are vertices in completely disjoint 5-cells. Each pentadecagram is a chord-path[lower-alpha 22] visiting 15 vertices belonging to three different 5-cells; the two pentadecagrams shown in the {30/8}=2{15/4} projection visit the six 5-cells that appear as six disjoint pentagrams in the {30/12}=6{5/2} projection.[lower-alpha 4]
- Two angles are required to specify the separation between two planes in 4-space. If the two angles are identical, the two planes are called isoclinic. In double rotations, points rotate within invariant central planes of rotation by some angle, and the entire invariant central plane of rotation also tilts sideways (in a completely orthogonal invariant central plane of rotation) by some angle. Therefore each vertex traverses a helical smooth curve called an isocline between two points in different central planes, while traversing an ordinary great circle in each of two completely orthogonal central planes (as the planes tilt relative to their original planes). If the two orthogonal angles are identical, the distance traveled along each great circle is the same, and the double rotation is called isoclinic (also a Clifford displacement). A rotation which takes isoclinic central planes to each other is an isoclinic rotation.
- The 5-cell, 8-cell and 120-cell all have tetrahedral vertex figures. In a 4-polytope with a tetrahedral vertex figure, a path along edges does not lie on an ordinary great circle in a single central plane: each successive edge lies in a different central plane than the previous edge. In the 120-cell the 30-edge circumferential path along edges follows a zig-zag skew Petrie polygon, which is not a great circle. However, there exists a 15-chord circumferential path that is a true geodesic great circle through those 15 vertices: but it is not an ordinary "flat" great circle of circumference 2𝝅𝑟, it is a helical isocline that bends in a circle in two completely orthogonal central planes at once, circling through four dimensions rather than confined to a two dimensional plane.[lower-alpha 20] The chord set of an isocline is called its Clifford polygon.[lower-alpha 24]
- The 120-cell contains 80 distinct 30-gon Petrie polygons, and can be partitioned into 20 disjoint 30-gon Petrie polygons.[lower-alpha 25] The Petrie 30-gon twists around its 0-gon great circle axis 8 times in the course of one circular orbit. Projected to the plane completely orthogonal to the 0-gon plane, the 120-cell Petrie polygon can be seen as a compound triacontagram {30/8}=2{15/4} of 30 #2 chords linking pairs of vertices that are 8 vertices apart on the circumference of the projection.[lower-alpha 10] The {30/8}-gram (with its #2 chord edges) is an alternate sequence of the same 30 vertices as the Petrie 30-gon (with its #1 chord edges).
- The chord-path of an isocline may be called the 4-polytope's Clifford polygon, as it is the skew polygram shape of the rotational circles traversed by the 4-polytope's vertices in its characteristic Clifford displacement.[lower-alpha 21]
- The regular skew 30-gon is the Petrie polygon of the 600-cell and its dual the 120-cell. The Petrie polygons of the 120-cell occur in the 600-cell as duals of the 30-cell Boerdijk–Coxeter helix rings (the Petrie polygons of the 600-cell):[lower-alpha 28] connecting their 30 tetrahedral cell centers together produces the Petrie polygons of the dual 120-cell, as noticed by Rolfdieter Frank (circa 2001). Thus he discovered that the vertex set of the 120-cell partitions into 20 non-intersecting Petrie polygons. This set of 20 disjoint Clifford parallel skew polygons is a discrete Hopf fibration of the 120-cell (just as their 20 dual 30-cell rings are a discrete fibration of the 600-cell).[lower-alpha 15]
- The Petrie polygon of a 3-polytope (polyhedron) with triangular faces (e.g. an icosahedron) can be seen as a linear strip of edge-bonded faces bent into a ring. Within that circular strip of edge-bonded triangles (10 in the case of the icosahedron) the Petrie polygon can be picked out as a skew polygon of edges zig-zagging (not circling) through the 2-space of the polyhedron's surface: alternately bending left and right, and slaloming around a great circle axis that passes through the triangles but does not intersect any vertices. The Petrie polygon of a 4-polytope (polychoron) with tetrahedral cells (e.g. a 600-cell) can be seen as a linear helix of face-bonded cells bent into a ring: a Boerdijk–Coxeter helix ring. Within that circular helix of face-bonded tetrahedra (30 in the case of the 600-cell) the skew Petrie polygon can be picked out as a helix of edges zig-zagging (not circling) through the 3-space of the polychoron's surface: alternately bending left and right, and spiraling around a great circle axis that passes through the tetrahedra but does not intersect any vertices.
- The 30-edge circumference of the 120-cell follows a skew Petrie polygon, not a great circle polygon. The Petrie polygon of any 4-polytope is a skew helix spiraling through the curved 3-space of the 4-polytope's surface.[lower-alpha 26] The 120-cell contains 80 distinct 30-edge Petrie polygons.[lower-alpha 23] Every chord in a 4-polytope inscribed in the 120-cell occurs as the distance between two vertices in one of those 80 30-vertex helical rings. There are exactly 15 distinct Pythagorean distances through 4-space between pairs of vertices in the helical ring, ranging from the 120-cell edge-length which links any two nearest vertices in the ring (the #1 chord), to the 120-cell axis-length (diameter) which links any two antipodal (most distant) vertices in the ring (the #15 chord).[lower-alpha 13]
- The 600-cell Petrie polygon is a helical ring which twists around its 0-gon great circle axis 11 times in the course of one circular orbit. Projected to the plane completely orthogonal to the 0-gon plane, the 600-cell Petrie polygon can be seen to be a triacontagram {30/11} of 30 #11 chords linking pairs of vertices that are 11 vertices apart on the circumference of the projection.[16] The {30/11}-gram (with its #11 chord edges) is an alternate sequence of the same 30 vertices as the Petrie 30-gon (with its #3 chord edges).
 The Petrie polygon of the inscribed 600-cells can be seen in this projection to the plane of a triacontagram {30/11}, a 30-gram of #11 chords. The 600-cell Petrie is a helical ring which winds around its own axis 11 times. This projection along the axis of the ring cylinder shows the 30 vertices 12° apart around the cylinder's circular cross section, with #11 chords connecting every 11th vertex on the circle. The 600-cell edges (#3 chords) which are the Petrie polygon edges are not shown in this illustration, but they could be drawn around the circumference, connecting every 3rd vertex.
The Petrie polygon of the inscribed 600-cells can be seen in this projection to the plane of a triacontagram {30/11}, a 30-gram of #11 chords. The 600-cell Petrie is a helical ring which winds around its own axis 11 times. This projection along the axis of the ring cylinder shows the 30 vertices 12° apart around the cylinder's circular cross section, with #11 chords connecting every 11th vertex on the circle. The 600-cell edges (#3 chords) which are the Petrie polygon edges are not shown in this illustration, but they could be drawn around the circumference, connecting every 3rd vertex. - The fractional square root chord lengths are given as decimal fractions where:
𝚽 ≈ 0.618 is the inverse golden ratio 1/φ
𝚫 = 1 - 𝚽 = 𝚽2 ≈ 0.382
𝜀 = √𝚫2/2 ≈ 0.073
and the 120-cell edge-length 1/φ2√2 is:
𝛇 = √𝜀 ≈ 0.270
For example:
𝛇 = √0.𝜀 = √0.073~ ≈ 0.270 - In the dodecahedral cell of the unit-radius 120-cell, the length of the edge (the #1 chord of the 120-cell) is 1/φ2√2 ≈ 0.270. The orange vertices lie at the Cartesian coordinates (±φ3√8, ±φ3√8, ±φ3√8) relative to origin at the cell center. They form a cube (dashed lines) of edge length 1/φ√2 ≈ 0.437 (the pentagon diagonal, and the #2 chord of the 120-cell). The face diagonals of the cube (not shown) of edge length 1/φ ≈ 0.618 are the edges of tetrahedral cells inscribed in the cube (600-cell edges, and the #3 chord of the 120-cell). The diameter of the dodecahedron is √3/φ√2 ≈ 0.757 (the cube diagonal, and the #4 chord of the 120-cell).
- The face pentagon diagonal (the #2 chord) is in the golden ratio φ ≈ 1.618 to the face pentagon edge (the 120-cell edge, the #1 chord).[lower-alpha 30]
- Each great hexagon edge is the axis of a zig-zag of 5 120-cell edges. The 120-cell's Petrie polygon is a helical zig-zag of 30 120-cell edges, spiraling around a 0-gon great circle axis that does not intersect any vertices.[lower-alpha 15] There are 5 great hexagons inscribed in each Petrie polygon, in five different central planes.[lower-alpha 12]
.svg.png.webp) Triacontagram {30/5}=5{6}, the 120-cell's skew Petrie 30-gon as a compound of 5 great hexagons.
Triacontagram {30/5}=5{6}, the 120-cell's skew Petrie 30-gon as a compound of 5 great hexagons. - The Petrie polygon of the 5-cell is the pentagon (5-gon), and the Petrie polygon of the 120-cell is the triacontagon (30-gon).[lower-alpha 23] Each 120-cell Petrie 30-gon lies completely orthogonal to six 5-cell Petrie 5-gons, which belong to six of the 120 disjoint regular 5-cells inscribed in the 120-cell.[lower-alpha 4]
- The sum of the squared lengths of all the distinct chords of any regular convex n-polytope of unit radius is the square of the number of vertices.[17]
- Dodecahedra emerge as visible features in the 120-cell, but they also occur in the 600-cell as interior polytopes.[19]
- In the 120-cell, each 24-cell belongs to two different 600-cells.[21] The 120-cell can be partitioned into 25 disjoint 24-cells.[22]
- The 10 tetrahedra in each dodecahedron overlap; but the 600 tetrahedra in each 600-cell do not, so each of the 10 must belong to a different 600-cell.
- Each 120-cell vertex figure is actually a low tetrahedral pyramid, an irregular 5-cell with a regular tetrahedron base.
- As we saw in the 600-cell, these 12 tetrahedra belong (in pairs) to the 6 icosahedral clusters of twenty tetrahedral cells which surround each cluster of five tetrahedral cells.
- Each regular great hexagon is shared by two 24-cells,[38] and each 24-cell is shared by two 600-cells.[21] It follows that any two 600-cells either share 16 great hexagons, or they are completely disjoint. All ten 600-cells share the same set of 200 irregular great dodecagon central planes. Any two completely disjoint 600-cells do so by occupying the alternate (disjoint) great hexagons in every great dodecagon plane.
- The diminishment of the 600-point 120-cell to a 480-point 4-polytope by removal of one if its 600-cells is analogous to the diminishment of the 120-point 600-cell by removal of one of its 5 disjoint inscribed 24-cells, creating the 96-point snub 24-cell. Similarly, the 8-cell tesseract can be seen as a 16-point diminished 24-cell from which one 8-point 16-cell has been removed.
Citations
- N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite Symmetry Groups, 11.5 Spherical Coxeter groups, p.249
- Matila Ghyka, The Geometry of Art and Life (1977), p.68
- Coxeter 1973, pp. 292–293, Table I(ii); "120-cell".
- Dechant 2021, p. 20, Remark 5.7, explains why not.[lower-alpha 5]
- Dechant 2021, Abstract; "[E]very 3D root system allows the construction of a corresponding 4D root system via an ‘induction theorem’. In this paper, we look at the icosahedral case of H3 → H4 in detail and perform the calculations explicitly. Clifford algebra is used to perform group theoretic calculations based on the versor theorem and the Cartan-Dieudonné theorem ... shed[ding] light on geometric aspects of the H4 root system (the 600-cell) as well as other related polytopes and their symmetries ... including the construction of the Coxeter plane, which is used for visualising the complementary pairs of invariant polytopes.... This approach therefore constitutes a more systematic and general way of performing calculations concerning groups, in particular reflection groups and root systems, in a Clifford algebraic framework."
- Mathematics and Its History, John Stillwell, 1989, 3rd edition 2010, ISBN 0-387-95336-1
- Stillwell 2001.
- Coxeter 1973, pp. 156–157, §8.7 Cartesian coordinates.
- Mamone, Pileio & Levitt 2010, p. 1442, Table 3.
- Mamone, Pileio & Levitt 2010, p. 1433, §4.1; A Cartesian 4-coordinate point (w,x,y,z) is a vector in 4D space from (0,0,0,0). Four-dimensional real space is a vector space: any two vectors can be added or multiplied by a scalar to give another vector. Quaternions extend the vectorial structure of 4D real space by allowing the multiplication of two 4D vectors and according to
- Coxeter 1973, p. 304, Table VI (iv): 𝐈𝐈 = {5,3,3}.
- Mamone, Pileio & Levitt 2010, pp. 1438–1439, §4.5 Regular Convex 4-Polytopes, Table 2, Symmetry operations; in symmetry group 𝛢4 the operation [15]𝑹q3,q3 is the 15 distinct simple rotations which comprise the pentagram isoclinic rotations of an individual 5-cell; in symmetry group 𝛨4 the operation [1200]𝑹q3,q13 is the 1200 distinct simple rotations which comprise the pentadecagram isoclinic rotations of the 120-cell, the 120-cell's characteristic rotation. Mamone's q3 corresponds to the #8 chord of the 120-cell, the 5-cell's √2.5 edge; q13 corresponds to the #1 chord of the 120-cell, its edge.
- Mamone, Pileio & Levitt 2010, pp. 1438–1439, §4.5 Regular Convex 4-Polytopes, Table 2, Symmetry group 𝛨4; the 120-cell has 7200 distinct simple rotations (and 7200 reflections).
- Coxeter 1973, pp. 300–301, Table V:(v) Simplified sections of {5,3,3} (edge 2𝝓−2√2 [radius 4]) beginning with a vertex.
- Coxeter 1973, p. 147, §8.1 The simple truncations of the general regular polytope; "At a point of contact, [elements of a regular polytope and elements of its dual in which it is inscribed in some manner] lie in completely orthogonal subspaces of the tangent hyperplane to the sphere [of reciprocation], so their only common point is the point of contact itself.... In fact, the [various] radii 0𝑹, 1𝑹, 2𝑹, ... determine the polytopes ... whose vertices are the centers of elements 𝐈𝐈0, 𝐈𝐈1, 𝐈𝐈2, ... of the original polytope."
- Sadoc 2001, pp. 577–578, §2.5 The 30/11 symmetry: an example of other kind of symmetries.
- Copher 2019, p. 6, §3.2 Theorem 3.4.
- Schleimer & Segerman 2013.
- Coxeter 1973, p. 298, Table V: (iii) Sections of {3,3,5} beginning with a vertex.
- Carlo H. Séquin (July 2005). Symmetrical Hamiltonian manifolds on regular 3D and 4D polytopes. Mathartfun.com. pp. 463–472. ISBN 9780966520163. Retrieved March 13, 2023.
- van Ittersum 2020, p. 435, §4.3.5 The two 600-cells circumscribing a 24-cell.
- Denney et al. 2020, p. 5, §2 The Labeling of H4.
- Coxeter 1973, p. 305, Table VII: Regular Compounds in Four Dimensions.
- Waegell & Aravind 2014, pp. 3–4, §2 Geometry of the 120-cell: rays and bases.
- Waegell & Aravind 2014, pp. 5–6.
- Sullivan 1991, pp. 4–5, The Dodecahedron.
- Coxeter et al. 1938, p. 4; "Just as a tetrahedron can be inscribed in a cube, so a cube can be inscribed in a dodecahedron. By reciprocation, this leads to an octahedron circumscribed about an icosahedron. In fact, each of the twelve vertices of the icosahedron divides an edge of the octahedron according to the "golden section". Given the icosahedron, the circumscribed octahedron can be chosen in five ways, giving a compound of five octahedra, which comes under our definition of stellated icosahedron. (The reciprocal compound, of five cubes whose vertices belong to a dodecahedron, is a stellated triacontahedron.) Another stellated icosahedron can at once be deduced, by stellating each octahedron into a stella octangula, thus forming a compound of ten tetrahedra. Further, we can choose one tetrahedron from each stella octangula, so as to derive a compound of five tetrahedra, which still has all the rotation symmetry of the icosahedron (i.e. the icosahedral group), although it has lost the reflections. By reflecting this figure in any plane of symmetry of the icosahedron, we obtain the complementary set of five tetrahedra. These two sets of five tetrahedra are enantiomorphous, i.e. not directly congruent, but related like a pair of shoes. [Such] a figure which possesses no plane of symmetry (so that it is enantiomorphous to its mirror-image) is said to be chiral."
- Koca, Al-Ajmi & Ozdes Koca 2011, pp. 986–988, 6. Dual of the snub 24-cell.
- Coxeter 1973, §1.8 Configurations.
- Coxeter 1991, p. 117.
- Sullivan 1991, p. 15, Other Properties of the 120-cell.
- Schleimer & Segerman 2013, p. 16, §6.1. Layers of dodecahedra.
- Coxeter 1970, pp. 19–23, §9. The 120-cell and the 600-cell.
- Schleimer & Segerman 2013, pp. 16–18, §6.2. Rings of dodecahedra.
- Banchoff 2013.
- Zamboj 2021, pp. 6–12, §2 Mathematical background.
- Zamboj 2021, pp. 23–29, §5 Hopf tori corresponding to circles on B2.
- Denney et al. 2020, p. 438.
- Chilton 1964.
- Dechant 2021, pp. 18–20, 6. The Coxeter Plane.
- Denney et al. 2020.
References
- Coxeter, H.S.M. (1973) [1948]. Regular Polytopes (3rd ed.). New York: Dover.
- Coxeter, H.S.M. (1991). Regular Complex Polytopes (2nd ed.). Cambridge: Cambridge University Press.
- Coxeter, H.S.M. (1995). Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivic (eds.). Kaleidoscopes: Selected Writings of H.S.M. Coxeter (2nd ed.). Wiley-Interscience Publication. ISBN 978-0-471-01003-6.
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Coxeter, H.S.M.; du Val, Patrick; Flather, H.T.; Petrie, J.F. (1938). The Fifty-Nine Icosahedra. Vol. 6. University of Toronto Studies (Mathematical Series).
- Coxeter, H.S.M. (1970), "Twisted Honeycombs", Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics, Providence, Rhode Island: American Mathematical Society, 4
- Stillwell, John (January 2001). "The Story of the 120-Cell" (PDF). Notices of the AMS. 48 (1): 17–25.
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation Archived 2005-03-22 at the Wayback Machine
- Davis, Michael W. (1985), "A hyperbolic 4-manifold", Proceedings of the American Mathematical Society, 93 (2): 325–328, doi:10.2307/2044771, ISSN 0002-9939, JSTOR 2044771, MR 0770546
- Denney, Tomme; Hooker, Da'Shay; Johnson, De'Janeke; Robinson, Tianna; Butler, Majid; Claiborne, Sandernishe (2020). "The geometry of H4 polytopes". Advances in Geometry. 20 (3): 433–444. arXiv:1912.06156v1. doi:10.1515/advgeom-2020-0005. S2CID 220367622.
- Steinbach, Peter (1997). "Golden fields: A case for the Heptagon". Mathematics Magazine. 70 (Feb 1997): 22–31. doi:10.1080/0025570X.1997.11996494. JSTOR 2691048.
- Copher, Jessica (2019). "Sums and Products of Regular Polytopes' Squared Chord Lengths". arXiv:1903.06971 [math.MG].
- Miyazaki, Koji (1990). "Primary Hypergeodesic Polytopes". International Journal of Space Structures. 5 (3–4): 309–323. doi:10.1177/026635119000500312. S2CID 113846838.
- van Ittersum, Clara (2020). "Symmetry groups of regular polytopes in three and four dimensions". TUDelft.
- Mamone, Salvatore; Pileio, Giuseppe; Levitt, Malcolm H. (2010). "Orientational Sampling Schemes Based on Four Dimensional Polytopes". Symmetry. 2 (3): 1423–1449. Bibcode:2010Symm....2.1423M. doi:10.3390/sym2031423.
- Sullivan, John M. (1991). "Generating and Rendering Four-Dimensional Polytopes". Mathematica Journal. 1 (3): 76–85.
- Waegell, Mordecai; Aravind, P.K. (10 Sep 2014). "Parity Proofs of the Kochen–Specker Theorem Based on the 120-Cell". Foundations of Physics. 44 (10): 1085–1095. arXiv:1309.7530v3. Bibcode:2014FoPh...44.1085W. doi:10.1007/s10701-014-9830-0. S2CID 254504443.
- Zamboj, Michal (8 Jan 2021). "Synthetic construction of the Hopf fibration in a double orthogonal projection of 4-space". Journal of Computational Design and Engineering. 8 (3): 836–854. arXiv:2003.09236v2. doi:10.1093/jcde/qwab018.
- Sadoc, Jean-Francois (2001). "Helices and helix packings derived from the {3,3,5} polytope". European Physical Journal E. 5: 575–582. doi:10.1007/s101890170040. S2CID 121229939.
- Chilton, B. L. (September 1964). "On the projection of the regular polytope {5,3,3} into a regular triacontagon". Canadian Mathematical Bulletin. 7 (3): 385–398. doi:10.4153/CMB-1964-037-9.
- Schleimer, Saul; Segerman, Henry (2013). "Puzzling the 120-cell". Notices Amer. Math. Soc. 62 (11): 1309–1316. arXiv:1310.3549. doi:10.1090/noti1297. S2CID 117636740.
- Banchoff, Thomas F. (2013). "Torus Decompostions of Regular Polytopes in 4-space". In Senechal, Marjorie (ed.). Shaping Space. Springer New York. pp. 257–266. doi:10.1007/978-0-387-92714-5_20. ISBN 978-0-387-92713-8.
- Koca, Mehmet; Ozdes Koca, Nazife; Al-Barwani, Muataz (2012). "Snub 24-Cell Derived from the Coxeter-Weyl Group W(D4)". Int. J. Geom. Methods Mod. Phys. 09 (8). arXiv:1106.3433. doi:10.1142/S0219887812500685. S2CID 119288632.
- Koca, Mehmet; Al-Ajmi, Mudhahir; Ozdes Koca, Nazife (2011). "Quaternionic representation of snub 24-cell and its dual polytope derived from E8 root system". Linear Algebra and Its Applications. 434 (4): 977–989. doi:10.1016/j.laa.2010.10.005. ISSN 0024-3795. S2CID 18278359.
- Dechant, Pierre-Philippe (2021). "Clifford Spinors and Root System Induction: H4 and the Grand Antiprism". Advances in Applied Clifford Algebras. Springer Science and Business Media. 31 (3). doi:10.1007/s00006-021-01139-2.
External links
- Weisstein, Eric W. "120-Cell". MathWorld.
- Olshevsky, George. "Hecatonicosachoron". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Klitzing, Richard. "4D uniform polytopes (polychora) o3o3o5x - hi".
- Der 120-Zeller (120-cell) Marco Möller's Regular polytopes in R4 (German)
- 120-cell explorer – A free interactive program that allows you to learn about a number of the 120-cell symmetries. The 120-cell is projected to 3 dimensions and then rendered using OpenGL.
- Construction of the Hyper-Dodecahedron
- YouTube animation of the construction of the 120-cell Gian Marco Todesco.
| H4 family polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 120-cell | rectified 120-cell |
truncated 120-cell |
cantellated 120-cell |
runcinated 120-cell |
cantitruncated 120-cell |
runcitruncated 120-cell |
omnitruncated 120-cell | ||||
| {5,3,3} | r{5,3,3} | t{5,3,3} | rr{5,3,3} | t0,3{5,3,3} | tr{5,3,3} | t0,1,3{5,3,3} | t0,1,2,3{5,3,3} | ||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
 |
 |
 |
 |
 |
 |
 | |||||
| 600-cell | rectified 600-cell |
truncated 600-cell |
cantellated 600-cell |
bitruncated 600-cell |
cantitruncated 600-cell |
runcitruncated 600-cell |
omnitruncated 600-cell | ||||
| {3,3,5} | r{3,3,5} | t{3,3,5} | rr{3,3,5} | 2t{3,3,5} | tr{3,3,5} | t0,1,3{3,3,5} | t0,1,2,3{3,3,5} | ||||