Order-7 triangular tiling

In geometry, the order-7 triangular tiling is a regular tiling of the hyperbolic plane with a Schläfli symbol of {3,7}.

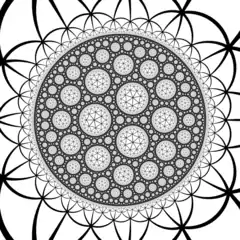
The {3,3,7} honeycomb has {3,7} vertex figures.
Order-7 triangular tiling
Order-7 triangular tiling
Poincaré disk model of the hyperbolic plane
TypeHyperbolic regular tiling
Vertex configuration37
Schläfli symbol{3,7}
Wythoff symbol7 | 3 2
Coxeter diagram
Symmetry group[7,3], (*732)
DualHeptagonal tiling
PropertiesVertex-transitive, edge-transitive, face-transitive

Hurwitz surfaces
Further information: Hurwitz surface

The symmetry group of the tiling is the (2,3,7) triangle group, and a fundamental domain for this action is the (2,3,7) Schwarz triangle. This is the smallest hyperbolic Schwarz triangle, and thus, by the proof of Hurwitz's automorphisms theorem, the tiling is the universal tiling that covers all Hurwitz surfaces (the Riemann surfaces with maximal symmetry group), giving them a triangulation whose symmetry group equals their automorphism group as Riemann surfaces.

The smallest of these is the Klein quartic, the most symmetric genus 3 surface, together with a tiling by 56 triangles, meeting at 24 vertices, with symmetry group the simple group of order 168, known as PSL(2,7). The resulting surface can in turn be polyhedrally immersed into Euclidean 3-space, yielding the small cubicuboctahedron.[1]

The dual order-3 heptagonal tiling has the same symmetry group, and thus yields heptagonal tilings of Hurwitz surfaces.


The symmetry group of the order-7 triangular tiling has fundamental domain the (2,3,7) Schwarz triangle, which yields this tiling.
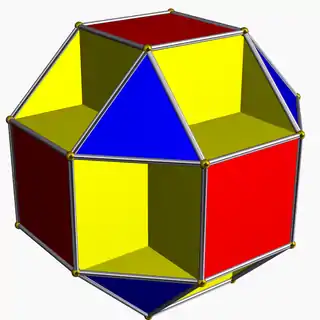The small cubicuboctahedron is a polyhedral immersion of the Klein quartic,[1] which, like all Hurwitz surfaces, is a quotient of this tiling.

It is related to two star-tilings by the same vertex arrangement: the order-7 heptagrammic tiling, {7/2,7}, and heptagrammic-order heptagonal tiling, {7,7/2}.

This tiling is topologically related as a part of sequence of regular polyhedra with Schläfli symbol {3,p}.

*n32 symmetry mutation of regular tilings: {3,n}
Spherical Euclid. Compact hyper. Paraco. Noncompact hyperbolic
3.3 33 34 35 36 37 38 3∞ 312i 39i 36i 33i

This tiling is a part of regular series {n,7}:

Tiles of the form {n,7}
Spherical Hyperbolic tilings

{2,7}
{3,7}
{4,7}
{5,7}
{6,7}
{7,7}
{8,7}
 ...
{∞,7}

From a Wythoff construction there are eight hyperbolic uniform tilings that can be based from the regular heptagonal tiling.

Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms.

Uniform heptagonal/triangular tilings
Symmetry: [7,3], (*732) [7,3]+, (732)
{7,3} t{7,3} r{7,3} t{3,7} {3,7} rr{7,3} tr{7,3} sr{7,3}
Uniform duals
V73 V3.14.14 V3.7.3.7 V6.6.7 V37 V3.4.7.4 V4.6.14 V3.3.3.3.7

See also
Wikimedia Commons has media related to Order-7 triangular tiling.

References
  1. (Richter) Note each face in the polyhedron consist of multiple faces in the tiling – two triangular faces constitute a square face and so forth, as per this explanatory image.
  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
  • "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
  • Richter, David A., How to Make the Mathieu Group M24, retrieved 2010-04-15
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.