Infinite-order apeirogonal tiling
In geometry, the infinite-order apeirogonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {∞,∞}, which means it has countably infinitely many apeirogons around all its ideal vertices.
| Infinite-order apeirogonal tiling | |
|---|---|
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic regular tiling |
| Vertex configuration | ∞∞ |
| Schläfli symbol | {∞,∞} |
| Wythoff symbol | ∞ | ∞ 2 ∞ ∞ | ∞ |
| Coxeter diagram | |
| Symmetry group | [∞,∞], (*∞∞2) [(∞,∞,∞)], (*∞∞∞) |
| Dual | self-dual |
| Properties | Vertex-transitive, edge-transitive, face-transitive |
Symmetry
This tiling represents the fundamental domains of *∞∞ symmetry.
Uniform colorings
This tiling can also be alternately colored in the [(∞,∞,∞)] symmetry from 3 generator positions.
| Domains | 0 | 1 | 2 |
|---|---|---|---|
 symmetry: [(∞,∞,∞)] |
 t0{(∞,∞,∞)} |
 t1{(∞,∞,∞)} |
 t2{(∞,∞,∞)} |
Related polyhedra and tiling
The union of this tiling and its dual can be seen as orthogonal red and blue lines here, and combined define the lines of a *2∞2∞ fundamental domain.

- a{∞,∞} or
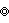



 =
= 


 ∪
∪ 



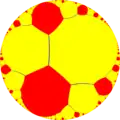
| Paracompact uniform tilings in [∞,∞] family | ||||||
|---|---|---|---|---|---|---|
= = |
= = |
= = |
= = |
= = |
= |
= |
 |
 |
 |
 |
 |
 |
 |
| {∞,∞} | t{∞,∞} | r{∞,∞} | 2t{∞,∞}=t{∞,∞} | 2r{∞,∞}={∞,∞} | rr{∞,∞} | tr{∞,∞} |
| Dual tilings | ||||||
 |
 |
 |
 |
 |
 |
 |
| V∞∞ | V∞.∞.∞ | V(∞.∞)2 | V∞.∞.∞ | V∞∞ | V4.∞.4.∞ | V4.4.∞ |
| Alternations | ||||||
| [1+,∞,∞] (*∞∞2) |
[∞+,∞] (∞*∞) |
[∞,1+,∞] (*∞∞∞∞) |
[∞,∞+] (∞*∞) |
[∞,∞,1+] (*∞∞2) |
[(∞,∞,2+)] (2*∞∞) |
[∞,∞]+ (2∞∞) |
 |
 |
 |
 |
 |
 | |
| h{∞,∞} | s{∞,∞} | hr{∞,∞} | s{∞,∞} | h2{∞,∞} | hrr{∞,∞} | sr{∞,∞} |
| Alternation duals | ||||||
 |
 |
 |
 | |||
| V(∞.∞)∞ | V(3.∞)3 | V(∞.4)4 | V(3.∞)3 | V∞∞ | V(4.∞.4)2 | V3.3.∞.3.∞ |
| Paracompact uniform tilings in [(∞,∞,∞)] family | ||||||
|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
| (∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) h2{∞,∞} |
(∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) h2{∞,∞} |
(∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) r{∞,∞} |
t(∞,∞,∞) t{∞,∞} |
| Dual tilings | ||||||
 |
 |
 |
 |
 |
 |
 |
| V∞∞ | V∞.∞.∞.∞ | V∞∞ | V∞.∞.∞.∞ | V∞∞ | V∞.∞.∞.∞ | V∞.∞.∞ |
| Alternations | ||||||
| [(1+,∞,∞,∞)] (*∞∞∞∞) |
[∞+,∞,∞)] (∞*∞) |
[∞,1+,∞,∞)] (*∞∞∞∞) |
[∞,∞+,∞)] (∞*∞) |
[(∞,∞,∞,1+)] (*∞∞∞∞) |
[(∞,∞,∞+)] (∞*∞) |
[∞,∞,∞)]+ (∞∞∞) |
 |
 |
 |
 |
 |
 |
 |
| Alternation duals | ||||||
 |
 |
 |
 |
 |
 |
|
| V(∞.∞)∞ | V(∞.4)4 | V(∞.∞)∞ | V(∞.4)4 | V(∞.∞)∞ | V(∞.4)4 | V3.∞.3.∞.3.∞ |
See also
Wikimedia Commons has media related to Infinite-order apeirogonal tiling.
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

