Gamma process

Also known as the (Moran-)Gamma Process,[1] the gamma process is a random process studied in mathematics, statistics, probability theory, and stochastics. The gamma process is a stochastic or random process consisting of independently distributed gamma distributions where $N(t)$ represents the number of event occurrences from time 0 to time $t$ . The gamma distribution has scale parameter $\gamma$ and shape parameter $\lambda$ , often written as $\Gamma (\gamma ,\lambda )$ .[1] Both $\gamma$ and $\lambda$ must be greater than 0. The gamma process is often written as $\Gamma (t,\gamma ,\lambda )$ where $t$ represents the time from 0. The process is a pure-jump increasing Lévy process with intensity measure $\nu (x)=\gamma x^{-1}\exp(-\lambda x),$ for all positive $x$ . Thus jumps whose size lies in the interval $[x,x+dx)$ occur as a Poisson process with intensity $\nu (x)\,dx.$ The parameter $\gamma$ controls the rate of jump arrivals and the scaling parameter $\lambda$ inversely controls the jump size. It is assumed that the process starts from a value 0 at t = 0 meaning $N(0)=0$ .

The gamma process is sometimes also parameterised in terms of the mean ( $\mu$ ) and variance ( $v$ ) of the increase per unit time, which is equivalent to $\gamma =\mu ^{2}/v$ and $\lambda =\mu /v$ .

Plain English definition

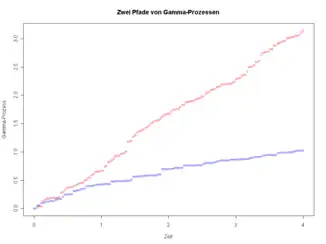
The gamma process is a process which measures the number of occurrences of independent gamma-distributed variables over a span of time. This image below displays two different gamma processes on from time 0 until time 4. The red process has more occurrences in the timeframe compared to the blue process because its shape parameter is larger than the blue shape parameter.

Gamma-Process

Properties

We use the Gamma function in these properties, so the reader should distinguish between $\Gamma (\cdot )$ (the Gamma function) and $\Gamma (t;\gamma ,\lambda )$ (the Gamma process). We will sometimes abbreviate the process as $X_{t}\equiv \Gamma (t;\gamma ,\lambda )$ .

Some basic properties of the gamma process are:

Marginal distribution

The marginal distribution of a gamma process at time $t$ is a gamma distribution with mean $\gamma t/\lambda$ and variance $\gamma t/\lambda ^{2}.$

That is, the probability distribution $f$ of the random variable $X_{t}$ is given by the density

f(x;t,\gamma ,\lambda )={\frac {\lambda ^{\gamma t}}{\Gamma (\gamma t)}}x^{\gamma t\,-\,1}e^{-\lambda x}.

Scaling

Multiplication of a gamma process by a scalar constant $\alpha$ is again a gamma process with different mean increase rate.

\alpha \Gamma (t;\gamma ,\lambda )\simeq \Gamma (t;\gamma ,\lambda /\alpha )

Adding independent processes

The sum of two independent gamma processes is again a gamma process.

\Gamma (t;\gamma _{1},\lambda )+\Gamma (t;\gamma _{2},\lambda )\simeq \Gamma (t;\gamma _{1}+\gamma _{2},\lambda )

Moments

The moment function helps mathematicians find expected values, variances, skewness, and kurtosis.

\operatorname {E} (X_{t}^{n})=\lambda ^{-n}\cdot {\frac {\Gamma (\gamma t+n)}{\Gamma (\gamma t)}},\ \quad n\geq 0,

where

\Gamma (z)

is the Gamma function.

Moment generating function

The moment generating function is the expected value of

\exp(tX)

where X is the random variable.

\operatorname {E} {\Big (}\exp(\theta X_{t}){\Big )}=\left(1-{\frac {\theta }{\lambda }}\right)^{-\gamma t},\ \quad \theta <\lambda

Correlation

Correlation displays the statistical relationship between any two gamma processes.

\operatorname {Corr} (X_{s},X_{t})={\sqrt {\frac {s}{t}}},\ s<t

, for any gamma process

X(t).

The gamma process is used as the distribution for random time change in the variance gamma process.

Literature

Lévy Processes and Stochastic Calculus by David Applebaum, CUP 2004, ISBN 0-521-83263-2.

References

Klenke, Achim, ed. (2008), "The Poisson Point Process", Probability Theory: A Comprehensive Course, London: Springer, pp. 525–542, doi:10.1007/978-1-84800-048-3_24, ISBN 978-1-84800-048-3, retrieved 2023-04-04

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[:0-1] Klenke, Achim, ed. (2008), "The Poisson Point Process", Probability Theory: A Comprehensive Course, London: Springer, pp. 525–542, doi:10.1007/978-1-84800-048-3_24, ISBN 978-1-84800-048-3, retrieved 2023-04-04

Stochastic processes
Discrete time	Bernoulli process Branching process Chinese restaurant process Galton–Watson process Independent and identically distributed random variables Markov chain Moran process Random walk Loop-erased Self-avoiding Biased Maximal entropy
Continuous time	Additive process Bessel process Birth–death process pure birth Brownian motion Bridge Excursion Fractional Geometric Meander Cauchy process Contact process Continuous-time random walk Cox process Diffusion process Empirical process Feller process Fleming–Viot process Gamma process Geometric process Hawkes process Hunt process Interacting particle systems Itô diffusion Itô process Jump diffusion Jump process Lévy process Local time Markov additive process McKean–Vlasov process Ornstein–Uhlenbeck process Poisson process Compound Non-homogeneous Schramm–Loewner evolution Semimartingale Sigma-martingale Stable process Superprocess Telegraph process Variance gamma process Wiener process Wiener sausage
Both	Branching process Galves–Löcherbach model Gaussian process Hidden Markov model (HMM) Markov process Martingale Differences Local Sub- Super- Random dynamical system Regenerative process Renewal process Stochastic chains with memory of variable length White noise
Fields and other	Dirichlet process Gaussian random field Gibbs measure Hopfield model Ising model Potts model Boolean network Markov random field Percolation Pitman–Yor process Point process Cox Poisson Random field Random graph
Time series models	Autoregressive conditional heteroskedasticity (ARCH) model Autoregressive integrated moving average (ARIMA) model Autoregressive (AR) model Autoregressive–moving-average (ARMA) model Generalized autoregressive conditional heteroskedasticity (GARCH) model Moving-average (MA) model
Financial models	Binomial options pricing model Black–Derman–Toy Black–Karasinski Black–Scholes Chan–Karolyi–Longstaff–Sanders (CKLS) Chen Constant elasticity of variance (CEV) Cox–Ingersoll–Ross (CIR) Garman–Kohlhagen Heath–Jarrow–Morton (HJM) Heston Ho–Lee Hull–White LIBOR market Rendleman–Bartter SABR volatility Vašíček Wilkie
Actuarial models	Bühlmann Cramér–Lundberg Risk process Sparre–Anderson
Queueing models	Bulk Fluid Generalized queueing network M/G/1 M/M/1 M/M/c
Properties	Càdlàg paths Continuous Continuous paths Ergodic Exchangeable Feller-continuous Gauss–Markov Markov Mixing Piecewise-deterministic Predictable Progressively measurable Self-similar Stationary Time-reversible
Limit theorems	Central limit theorem Donsker's theorem Doob's martingale convergence theorems Ergodic theorem Fisher–Tippett–Gnedenko theorem Large deviation principle Law of large numbers (weak/strong) Law of the iterated logarithm Maximal ergodic theorem Sanov's theorem Zero–one laws (Blumenthal, Borel–Cantelli, Engelbert–Schmidt, Hewitt–Savage, Kolmogorov, Lévy)
Inequalities	Burkholder–Davis–Gundy Doob's martingale Doob's upcrossing Kunita–Watanabe Marcinkiewicz–Zygmund
Tools	Cameron–Martin formula Convergence of random variables Doléans-Dade exponential Doob decomposition theorem Doob–Meyer decomposition theorem Doob's optional stopping theorem Dynkin's formula Feynman–Kac formula Filtration Girsanov theorem Infinitesimal generator Itô integral Itô's lemma Karhunen–Loève theorem Kolmogorov continuity theorem Kolmogorov extension theorem Lévy–Prokhorov metric Malliavin calculus Martingale representation theorem Optional stopping theorem Prokhorov's theorem Quadratic variation Reflection principle Skorokhod integral Skorokhod's representation theorem Skorokhod space Snell envelope Stochastic differential equation Tanaka Stopping time Stratonovich integral Uniform integrability Usual hypotheses Wiener space Classical Abstract
Disciplines	Actuarial mathematics Control theory Econometrics Ergodic theory Extreme value theory (EVT) Large deviations theory Mathematical finance Mathematical statistics Probability theory Queueing theory Renewal theory Ruin theory Signal processing Statistics Stochastic analysis Time series analysis Machine learning
List of topics Category