List of Wenninger polyhedron models

This is an indexed list of the uniform and stellated polyhedra from the book Polyhedron Models, by Magnus Wenninger.

The book was written as a guide book to building polyhedra as physical models. It includes templates of face elements for construction and helpful hints in building, and also brief descriptions on the theory behind these shapes. It contains the 75 nonprismatic uniform polyhedra, as well as 44 stellated forms of the convex regular and quasiregular polyhedra.

Models listed here can be cited as "Wenninger Model Number N", or WN for brevity.

The polyhedra are grouped in 5 tables: Regular (1–5), Semiregular (6–18), regular star polyhedra (20–22,41), Stellations and compounds (19–66), and uniform star polyhedra (67–119). The four regular star polyhedra are listed twice because they belong to both the uniform polyhedra and stellation groupings.

Platonic solids (regular convex polyhedra) W1 to W5
Index Name Picture Dual name Dual picture Wythoff symbol Vertex figure
and Schläfli symbol		 Symmetry group U# K# V E F Faces by type
1 Tetrahedron Tetrahedron 3|2 3
{3,3}		 Td U01 K06 4 6 4 4{3}
2 Octahedron Hexahedron 4|2 3
{3,4}		 Oh U05 K10 6 12 8 8{3}
3 Hexahedron (Cube) Octahedron 3|2 4
{4,3}		 Oh U06 K11 8 12 6 6{4}
4 Icosahedron Dodecahedron 5|2 3
{3,5}		 Ih U22 K27 12 30 20 20{3}
5 Dodecahedron Icosahedron 3|2 5
{5,3}		 Ih U23 K28 20 30 12 12{5}

Archimedean solids (Semiregular) W6 to W18
Index Name Picture Dual name Dual picture Wythoff symbol Vertex figure Symmetry group U# K# V E F Faces by type
6 Truncated tetrahedron triakis tetrahedronTriakis tetrahedron 2 3|3
3.6.6		 Td U02 K07 12 18 8 4{3} + 4{6}
7 Truncated octahedron 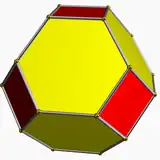tetrakis hexahedronTetrakis hexahedron 2 4|3
4.6.6		 Oh U08 K13 14 36 24 6{4} + 8{6}
8 Truncated hexahedron triakis octahedronTriakis octahedron 2 3|4
3.8.8		 Oh U09 K14 24 36 14 8{3} + 6{8}
9 Truncated icosahedron pentakis dodecahedronPentakis dodecahedron 2 5|3
5.6.6		 Ih U25 K30 60 90 32 12{5} + 20{6}
10 Truncated dodecahedron triakis icosahedronTriakis icosahedron 2 3|5
3.10.10		 Ih U26 K31 60 90 32 20{3} + 12{10}
11 Cuboctahedron 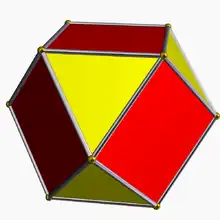rhombic dodecahedronRhombic dodecahedron 2|3 4
3.4.3.4		 Oh U07 K12 12 24 14 8{3} + 6{4}
12 Icosidodecahedron rhombic triacontahedronRhombic triacontahedron 2|3 5
3.5.3.5		 Ih U24 K29 30 60 32 20{3} + 12{5}
13 Small rhombicuboctahedron deltoidal icositetrahedronDeltoidal icositetrahedron 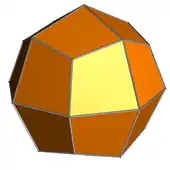3 4|2
3.4.4.4		 Oh U10 K15 24 48 26 8{3}+(6+12){4}
14 Small rhombicosidodecahedron deltoidal hexecontahedronDeltoidal hexecontahedron 3 5|2
3.4.5.4		 Ih U27 K32 60 120 62 20{3} + 30{4} + 12{5}
15 Truncated cuboctahedron
(Great rhombicuboctahedron)		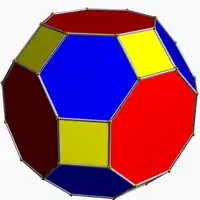 disdyakis dodecahedronDisdyakis dodecahedron 2 3 4|
4.6.8		 Oh U11 K16 48 72 26 12{4} + 8{6} + 6{8}
16 Truncated icosidodecahedron
(Great rhombicosidodecahedron)		 disdyakis triacontahedronDisdyakis triacontahedron 2 3 5|
4.6.10		 Ih U28 K33 120 180 62 30{4} + 20{6} + 12{10}
17 Snub cube pentagonal icositetrahedronPentagonal icositetrahedron |2 3 4
3.3.3.3.4		 O U12 K17 24 60 38 (8 + 24){3} + 6{4}
18 Snub dodecahedron pentagonal hexecontahedronPentagonal hexecontahedron |2 3 5
3.3.3.3.5		 I U29 K34 60 150 92 (20 + 60){3} + 12{5}

Kepler–Poinsot polyhedra (Regular star polyhedra) W20, W21, W22 and W41
Index Name Picture Dual name Dual picture Wythoff symbol Vertex figure
and Schläfli symbol		 Symmetry group U# K# V E F Faces by type
20 Small stellated dodecahedron Great dodecahedron 5|25/2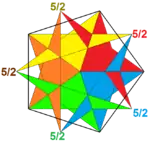
{5/2,5}		 Ih U34 K39 12 30 12 12{5/2}
21 Great dodecahedron Small stellated dodecahedron 5/2|2 5
{5,5/2}		 Ih U35 K40 12 30 12 12{5}
22 Great stellated dodecahedron Great icosahedron 3|25/2
{5/2,3}		 Ih U52 K57 20 30 12 12{5/2}
41 Great icosahedron
(16th stellation of icosahedron)		 Great stellated dodecahedron 5/2|2 3
{3,5/2}		 Ih U53 K58 12 30 20 20{3}

Stellations: models W19 to W66

Stellations of octahedron
Index Name Symmetry group Picture Facets
2 Octahedron
(regular)		 Oh
19 Stellated octahedron
(Compound of two tetrahedra)		 Oh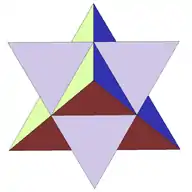

Stellations of dodecahedron
Index Name Symmetry group Picture Facets
5 Dodecahedron (regular) Ih
20 Small stellated dodecahedron (regular)
(First stellation of dodecahedron)		 Ih
21 Great dodecahedron (regular)
(Second stellation of dodecahedron)		 Ih
22 Great stellated dodecahedron (regular)
(Third stellation of dodecahedron)		 Ih

Stellations of icosahedron
Index Name Symmetry group Picture Facets
4 Icosahedron (regular) Ih
23 Compound of five octahedra
(First compound stellation of icosahedron)		 Ih
24 Compound of five tetrahedra
(Second compound stellation of icosahedron)		 I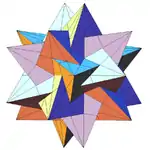
25 Compound of ten tetrahedra
(Third compound stellation of icosahedron)		 Ih
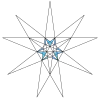26 Small triambic icosahedron
(First stellation of icosahedron)
(Triakis icosahedron)		 Ih
27 Second stellation of icosahedron Ih
28 Excavated dodecahedron
(Third stellation of icosahedron)		 Ih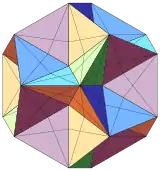
29 Fourth stellation of icosahedron Ih
30 Fifth stellation of icosahedron Ih
31 Sixth stellation of icosahedron Ih
32 Seventh stellation of icosahedron Ih
33 Eighth stellation of icosahedron Ih
34 Ninth stellation of icosahedron
Great triambic icosahedron
 Ih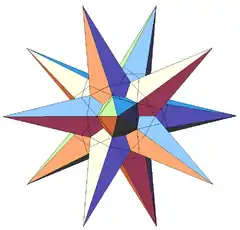
35 Tenth stellation of icosahedron I
36 Eleventh stellation of icosahedron I
37 Twelfth stellation of icosahedron Ih
38 Thirteenth stellation of icosahedron I
39 Fourteenth stellation of icosahedron I
40 Fifteenth stellation of icosahedron I
41 Great icosahedron (regular)
(Sixteenth stellation of icosahedron)		 Ih
42 Final stellation of the icosahedron Ih

Stellations of cuboctahedron
Index Name Symmetry group Picture Facets (octahedral planes) Facets (cube planes)
11 Cuboctahedron (regular) Oh
43 Compound of cube and octahedron
(First stellation of cuboctahedron)		 Oh
44 Second stellation of cuboctahedron Oh
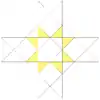45 Third stellation of cuboctahedron Oh
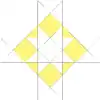46 Fourth stellation of cuboctahedron Oh

Stellations of icosidodecahedron
Index Name Symmetry group Picture Facets (icosahedral planes) Facets (dodecahedral planes)
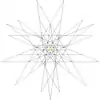
12 Icosidodecahedron
(regular)		 Ih
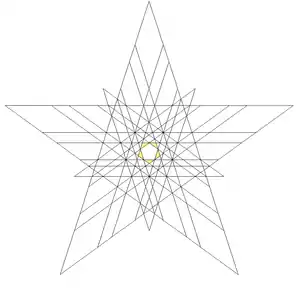
47 (First stellation of icosidodecahedron)
Compound of dodecahedron and icosahedron		 Ih
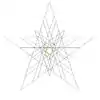
48 Second stellation of icosidodecahedron Ih
49 Third stellation of icosidodecahedron Ih
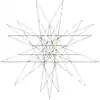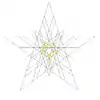50 Fourth stellation of icosidodecahedron
(Compound of small stellated dodecahedron
and triakis icosahedron)		 Ih
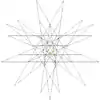51 Fifth stellation of icosidodecahedron
(Compound of small stellated dodecahedron
and five octahedra)		 Ih
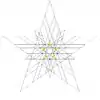52 Sixth stellation of icosidodecahedron Ih
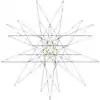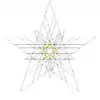53 Seventh stellation of icosidodecahedron Ih
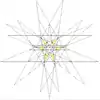54 Eighth stellation of icosidodecahedron
(Compound of five tetrahedra
and great dodecahedron)		 I
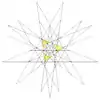55 Ninth stellation of icosidodecahedron Ih
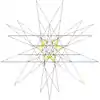56 Tenth stellation of icosidodecahedron Ih
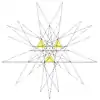57 Eleventh stellation of icosidodecahedron Ih
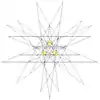58 Twelfth stellation of icosidodecahedron Ih
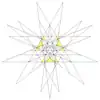59 Thirteenth stellation of icosidodecahedron Ih
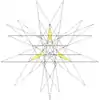60 Fourteenth stellation of icosidodecahedron Ih
61 Compound of great stellated dodecahedron and great icosahedron Ih
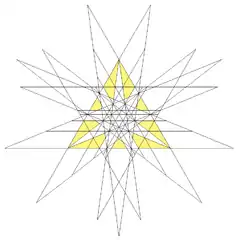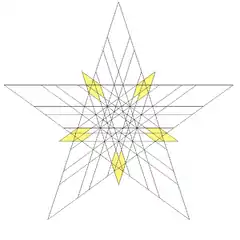62 Fifteenth stellation of icosidodecahedron Ih
63 Sixteenth stellation of icosidodecahedron Ih
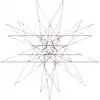64 Seventeenth stellation of icosidodecahedron Ih
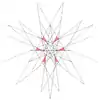65 Eighteenth stellation of icosidodecahedron Ih
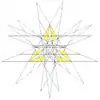66 Nineteenth stellation of icosidodecahedron Ih

Uniform nonconvex solids W67 to W119
Index Name Picture Dual name Dual picture Wythoff symbol Vertex figure Symmetry group U# K# V E F Faces by type
67TetrahemihexahedronTetrahemihexacron3/23|2
4.3/2.4.3		TdU04K0961274{3}+3{4}
68OctahemioctahedronOctahemioctacron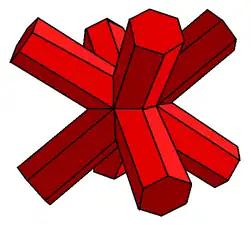3/23|3
6.3/2.6.3		OhU03K081224128{3}+4{6}
69Small cubicuboctahedron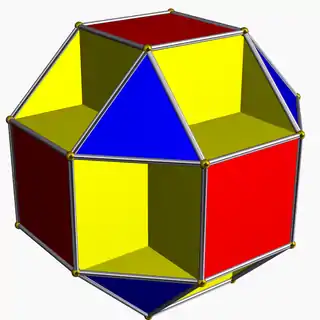Small hexacronic icositetrahedron3/24|4
8.3/2.8.4		OhU13K182448208{3}+6{4}+6{8}
70Small ditrigonal icosidodecahedronSmall triambic icosahedron3|5/23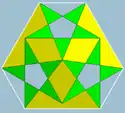
(5/2.3)3		IhU30K3520603220{3}+12{5/2}
71Small icosicosidodecahedronSmall icosacronic hexecontahedron5/23|3
6.5/2.6.3		IhU31K36601205220{3}+12{5/2}+20{6}
72Small dodecicosidodecahedronSmall dodecacronic hexecontahedron3/25|5
10.3/2.10.5		IhU33K38601204420{3}+12{5}+12{10}
73DodecadodecahedronMedial rhombic triacontahedron2|5/25
(5/2.5)2		IhU36K4130602412{5}+12{5/2}
74Small rhombidodecahedronSmall rhombidodecacron25/25|
10.4.10/9.4/3		IhU39K44601204230{4}+12{10}
75Truncated great dodecahedron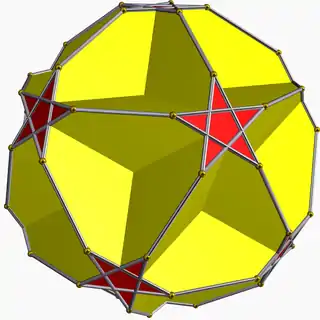Small stellapentakis dodecahedron25/2|5
10.10.5/2		IhU37K4260902412{5/2}+12{10}
76RhombidodecadodecahedronMedial deltoidal hexecontahedron5/25|2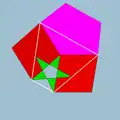
4.5/2.4.5		IhU38K43601205430{4}+12{5}+12{5/2}
77Great cubicuboctahedronGreat hexacronic icositetrahedron3 4|4/3
8/3.3.8/3.4		OhU14K192448208{3}+6{4}+6{8/3}
78CubohemioctahedronHexahemioctacron4/34|3
6.4/3.6.4		OhU15K201224106{4}+4{6}
79Cubitruncated cuboctahedron
(Cuboctatruncated cuboctahedron)		Tetradyakis hexahedron4/33 4|
8/3.6.8		OhU16K214872208{6}+6{8}+6{8/3}
80Ditrigonal dodecadodecahedronMedial triambic icosahedron3|5/35
(5/3.5)3		IhU41K4620602412{5}+12{5/2}
81Great ditrigonal dodecicosidodecahedronGreat ditrigonal dodecacronic hexecontahedron3 5|5/3
10/3.3.10/3.5		IhU42K47601204420{3}+12{5}+12{10/3}
82Small ditrigonal dodecicosidodecahedronSmall ditrigonal dodecacronic hexecontahedron5/33|5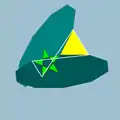
10.5/3.10.3		IhU43K48601204420{3}+12{5/2}+12{10}
83IcosidodecadodecahedronMedial icosacronic hexecontahedron5/35|3
6.5/3.6.5		IhU44K49601204412{5}+12{5/2}+20{6}
84Icositruncated dodecadodecahedron
(Icosidodecatruncated icosidodecahedron)		Tridyakis icosahedron5/33 5|
10/3.6.10		IhU45K501201804420{6}+12{10}+12{10/3}
85Nonconvex great rhombicuboctahedron
(Quasirhombicuboctahedron)		Great deltoidal icositetrahedron3/24|2
4.3/2.4.4		OhU17K222448268{3}+(6+12){4}
86Small rhombihexahedronSmall rhombihexacron3/22 4|
4.8.4/3.8		OhU18K2324481812{4}+6{8}
87Great ditrigonal icosidodecahedronGreat triambic icosahedron3/2|3 5
(5.3.5.3.5.3)/2		IhU47K5220603220{3}+12{5}
88Great icosicosidodecahedronGreat icosacronic hexecontahedron3/25|3
6.3/2.6.5		IhU48K53601205220{3}+12{5}+20{6}
89Small icosihemidodecahedronSmall icosihemidodecacron3/23|5
10.3/2.10.3		IhU49K5430602620{3}+6{10}
90Small dodecicosahedronSmall dodecicosacron3/23 5|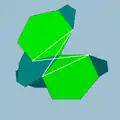
10.6.10/9.6/5		IhU50K55601203220{6}+12{10}
91Small dodecahemidodecahedronSmall dodecahemidodecacron5/45|5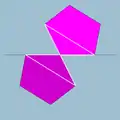
10.5/4.10.5		IhU51K5630601812{5}+6{10}
92Stellated truncated hexahedron
(Quasitruncated hexahedron)		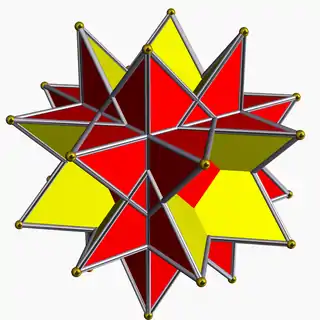Great triakis octahedron2 3|4/3
8/3.8/3.3		OhU19K242436148{3}+6{8/3}
93Great truncated cuboctahedron
(Quasitruncated cuboctahedron)		Great disdyakis dodecahedron4/32 3|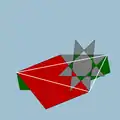
8/3.4.6		OhU20K2548722612{4}+8{6}+6{8/3}
94Great icosidodecahedronGreat rhombic triacontahedron2|5/23
(5/2.3)2		IhU54K5930603220{3}+12{5/2}
95Truncated great icosahedronGreat stellapentakis dodecahedron25/2|3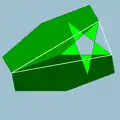
6.6.5/2		IhU55K6060903212{5/2}+20{6}
96RhombicosahedronRhombicosacron25/23|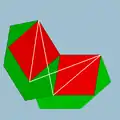
6.4.6/5.4/3		IhU56K61601205030{4}+20{6}
97Small stellated truncated dodecahedron
(Quasitruncated small stellated dodecahedron)		Great pentakis dodecahedron2 5|5/3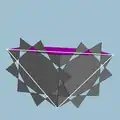
10/3.10/3.5		IhU58K6360902412{5}+12{10/3}
98Truncated dodecadodecahedron
(Quasitruncated dodecahedron)		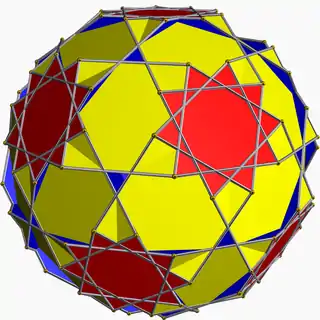Medial disdyakis triacontahedron5/32 5|
10/3.4.10		IhU59K641201805430{4}+12{10}+12{10/3}
99Great dodecicosidodecahedronGreat dodecacronic hexecontahedron5/23|5/3
10/3.5/2.10/3.3		IhU61K66601204420{3}+12{5/2}+12{10/3}
100Small dodecahemicosahedronSmall dodecahemicosacron5/35/2|3
6.5/3.6.5/2		IhU62K6730602212{5/2}+10{6}
101Great dodecicosahedronGreat dodecicosacron5/35/23|
6.10/3.6/5.10/7		IhU63K68601203220{6}+12{10/3}
102Great dodecahemicosahedronGreat dodecahemicosacron5/45|3
6.5/4.6.5		IhU65K7030602212{5}+10{6}
103Great rhombihexahedronGreat rhombihexacron4/33/22|
4.8/3.4/3.8/5		OhU21K2624481812{4}+6{8/3}
104Great stellated truncated dodecahedron
(Quasitruncated great stellated dodecahedron)		Great triakis icosahedron2 3|5/3
10/3.10/3.3		IhU66K7160903220{3}+12{10/3}
105Nonconvex great rhombicosidodecahedron
(Quasirhombicosidodecahedron)		Great deltoidal hexecontahedron5/33|2
4.5/3.4.3		IhU67K72601206220{3}+30{4}+12{5/2}
106Great icosihemidodecahedronGreat icosihemidodecacron3 3|5/3
10/3.3/2.10/3.3		IhU71K7630602620{3}+6{10/3}
107Great dodecahemidodecahedronGreat dodecahemidodecacron5/35/2|5/3
10/3.5/3.10/3.5/2		IhU70K7530601812{5/2}+6{10/3}
108Great truncated icosidodecahedron
(Great quasitruncated icosidodecahedron)		Great disdyakis triacontahedron5/32 3|
10/3.4.6		IhU68K731201806230{4}+20{6}+12{10/3}
109Great rhombidodecahedronGreat rhombidodecacron3/25/32|
4.10/3.4/3.10/7		IhU73K78601204230{4}+12{10/3}
110Small snub icosicosidodecahedronSmall hexagonal hexecontahedron|5/23 3
3.3.3.3.3.5/2		IhU32K3760180112(40+60){3}+12{5/2}
111Snub dodecadodecahedronMedial pentagonal hexecontahedron|25/25
3.3.5/2.3.5		IU40K45601508460{3}+12{5}+12{5/2}
112Snub icosidodecadodecahedron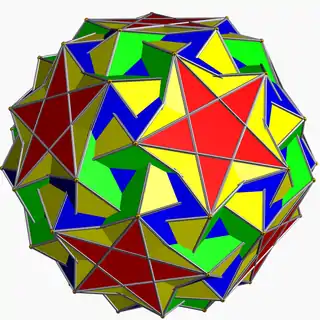Medial hexagonal hexecontahedron|5/33 5
3.3.3.3.5.5/3		IU46K5160180104(20+6){3}+12{5}+12{5/2}
113Great inverted snub icosidodecahedronGreat inverted pentagonal hexecontahedron|5/32 3
3.3.3.3.5/3		IU69K746015092(20+60){3}+12{5/2}
114Inverted snub dodecadodecahedron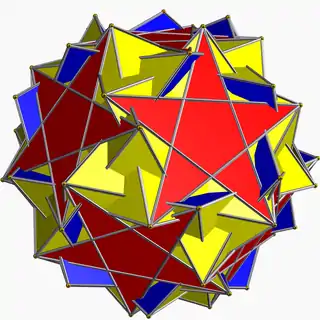Medial inverted pentagonal hexecontahedron|5/32 5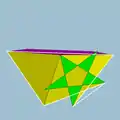
3.5/3.3.3.5		IU60K65601508460{3}+12{5}+12{5/2}
115Great snub dodecicosidodecahedronGreat hexagonal hexecontahedron|5/35/23
3.5/3.3.5/2.3.3		IU64K6960180104(20+60){3}+(12+12){5/2}
116Great snub icosidodecahedronGreat pentagonal hexecontahedron|25/25/2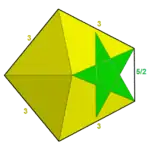
3.3.3.3.5/2		IU57K626015092(20+60){3}+12{5/2}
117Great retrosnub icosidodecahedronGreat pentagrammic hexecontahedron|3/25/32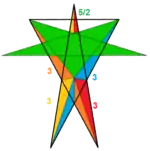
(3.3.3.3.5/2)/2		IU74K796015092(20+60){3}+12{5/2}
118Small retrosnub icosicosidodecahedronSmall hexagrammic hexecontahedron|3/23/25/2
(3.3.3.3.3.5/2)/2		IhU72K7718060112(40+60){3}+12{5/2}
119Great dirhombicosidodecahedronGreat dirhombicosidodecacron|3/25/335/2
(4.5/3.4.3.4.5/2.4.3/2)/2		IhU75K806024012440{3}+60{4}+24{5/2}

See also

References
  • Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
    • Errata
      • In Wenninger, the vertex figure for W90 is incorrectly shown as having parallel edges.
  • Wenninger, Magnus (1979). Spherical Models. Cambridge University Press. ISBN 0-521-29432-0.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.