Icosahedral honeycomb
In geometry, the icosahedral honeycomb is one of four compact, regular, space-filling tessellations (or honeycombs) in hyperbolic 3-space. With Schläfli symbol {3,5,3}, there are three icosahedra around each edge, and 12 icosahedra around each vertex, in a regular dodecahedral vertex figure.
| Icosahedral honeycomb | |
|---|---|
 Poincaré disk model | |
| Type | Hyperbolic regular honeycomb Uniform hyperbolic honeycomb |
| Schläfli symbol | {3,5,3} |
| Coxeter diagram | |
| Cells | {5,3} (regular icosahedron) |
| Faces | {3} (triangle) |
| Edge figure | {3} (triangle) |
| Vertex figure |  dodecahedron |
| Dual | Self-dual |
| Coxeter group | J3, [3,5,3] |
| Properties | Regular |
A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.
Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.
Description
The dihedral angle of a regular icosahedron is around 138.2°, so it is impossible to fit three icosahedra around an edge in Euclidean 3-space. However, in hyperbolic space, properly scaled icosahedra can have dihedral angles of exactly 120 degrees, so three of those can fit around an edge.

Related regular honeycombs
There are four regular compact honeycombs in 3D hyperbolic space:
 {5,3,4} |
 {4,3,5} |
 {3,5,3} |
 {5,3,5} |
Related regular polytopes and honeycombs
It is a member of a sequence of regular polychora and honeycombs {3,p,3} with deltrahedral cells:
| {3,p,3} polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | S3 | H3 | |||||||||
| Form | Finite | Compact | Paracompact | Noncompact | |||||||
| {3,p,3} | {3,3,3} | {3,4,3} | {3,5,3} | {3,6,3} | {3,7,3} | {3,8,3} | ... {3,∞,3} | ||||
| Image |  |
 |
 |
 |
 |
 |
 | ||||
| Cells |  {3,3} |
 {3,4} |
 {3,5} |
 {3,6} |
 {3,7} |
 {3,8} |
 {3,∞} | ||||
| Vertex figure |
 {3,3} |
 {4,3} |
 {5,3} |
 {6,3} |
 {7,3} |
 {8,3} |
 {∞,3} | ||||
It is also a member of a sequence of regular polychora and honeycombs {p,5,p}, with vertex figures composed of pentagons:
| {p,5,p} regular honeycombs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | H3 | ||||||||||
| Form | Compact | Noncompact | |||||||||
| Name | {3,5,3} | {4,5,4} | {5,5,5} | {6,5,6} | {7,5,7} | {8,5,8} | ...{∞,5,∞} | ||||
| Image |  |
 |
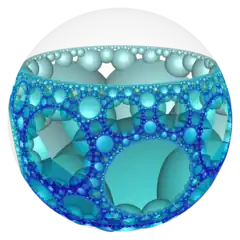 |
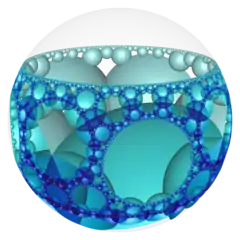 |
 | ||||||
| Cells {p,5} |
 {3,5} |
 {4,5} |
 {5,5} |
 {6,5} |
 {7,5} |
 {8,5} |
 {∞,5} | ||||
| Vertex figure {5,p} |
 {5,3} |
 {5,4} |
 {5,5} |
 {5,6} |
 {5,7} |
 {5,8} |
 {5,∞} | ||||
Uniform honeycombs
There are nine uniform honeycombs in the [3,5,3] Coxeter group family, including this regular form as well as the bitruncated form, t1,2{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , also called truncated dodecahedral honeycomb, each of whose cells are truncated dodecahedra.
, also called truncated dodecahedral honeycomb, each of whose cells are truncated dodecahedra.
| {3,5,3} |
t1{3,5,3} |
t0,1{3,5,3} |
t0,2{3,5,3} |
t0,3{3,5,3} |
|---|---|---|---|---|
 |
 |
 |
 |
 |
| t1,2{3,5,3} |
t0,1,2{3,5,3} |
t0,1,3{3,5,3} |
t0,1,2,3{3,5,3} | |
 |
 |
 |
 |
Rectified icosahedral honeycomb
| Rectified icosahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | r{3,5,3} or t1{3,5,3} |
| Coxeter diagram | |
| Cells | r{3,5} {5,3} |
| Faces | triangle {3} pentagon {5} |
| Vertex figure |  triangular prism |
| Coxeter group | , [3,5,3] |
| Properties | Vertex-transitive, edge-transitive |
The rectified icosahedral honeycomb, t1{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has alternating dodecahedron and icosidodecahedron cells, with a triangular prism vertex figure:
, has alternating dodecahedron and icosidodecahedron cells, with a triangular prism vertex figure:


Perspective projections from center of Poincaré disk model
Related honeycomb
There are four rectified compact regular honeycombs:
| Image |  |
 |
 |
 |
|---|---|---|---|---|
| Symbols | r{5,3,4} |
r{4,3,5} |
r{3,5,3} |
r{5,3,5} |
| Vertex figure |
 |
 |
 |
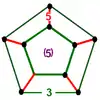 |
Truncated icosahedral honeycomb
| Truncated icosahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | t{3,5,3} or t0,1{3,5,3} |
| Coxeter diagram | |
| Cells | t{3,5} {5,3} |
| Faces | pentagon {5} hexagon {6} |
| Vertex figure |  triangular pyramid |
| Coxeter group | , [3,5,3] |
| Properties | Vertex-transitive |
The truncated icosahedral honeycomb, t0,1{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has alternating dodecahedron and truncated icosahedron cells, with a triangular pyramid vertex figure.
, has alternating dodecahedron and truncated icosahedron cells, with a triangular pyramid vertex figure.

Related honeycombs
| Image |  |
 |
 |
 |
|---|---|---|---|---|
| Symbols | t{5,3,4} |
t{4,3,5} |
t{3,5,3} |
t{5,3,5} |
| Vertex figure |
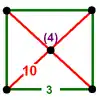 |
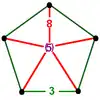 |
 |
 |
Bitruncated icosahedral honeycomb
| Bitruncated icosahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | 2t{3,5,3} or t1,2{3,5,3} |
| Coxeter diagram | |
| Cells | t{5,3} |
| Faces | triangle {3} decagon {10} |
| Vertex figure |  tetragonal disphenoid |
| Coxeter group | , [[3,5,3]] |
| Properties | Vertex-transitive, edge-transitive, cell-transitive |
The bitruncated icosahedral honeycomb, t1,2{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has truncated dodecahedron cells with a tetragonal disphenoid vertex figure.
, has truncated dodecahedron cells with a tetragonal disphenoid vertex figure.

Related honeycombs
| Image |  |
 |
 |
|---|---|---|---|
| Symbols | 2t{4,3,5} |
2t{3,5,3} |
2t{5,3,5} |
| Vertex figure |
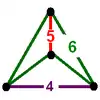 |
 |
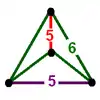 |
Cantellated icosahedral honeycomb
| Cantellated icosahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | rr{3,5,3} or t0,2{3,5,3} |
| Coxeter diagram | |
| Cells | rr{3,5} r{5,3} {}x{3} |
| Faces | triangle {3} square {4} pentagon {5} |
| Vertex figure | 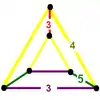 wedge |
| Coxeter group | , [3,5,3] |
| Properties | Vertex-transitive |
The cantellated icosahedral honeycomb, t0,2{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has rhombicosidodecahedron, icosidodecahedron, and triangular prism cells, with a wedge vertex figure.
, has rhombicosidodecahedron, icosidodecahedron, and triangular prism cells, with a wedge vertex figure.

Related honeycombs
| Four cantellated regular compact honeycombs in H3 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Cantitruncated icosahedral honeycomb
| Cantitruncated icosahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | tr{3,5,3} or t0,1,2{3,5,3} |
| Coxeter diagram | |
| Cells | tr{3,5} t{5,3} {}x{3} |
| Faces | triangle {3} square {4} hexagon {6} decagon {10} |
| Vertex figure |  mirrored sphenoid |
| Coxeter group | , [3,5,3] |
| Properties | Vertex-transitive |
The cantitruncated icosahedral honeycomb, t0,1,2{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has truncated icosidodecahedron, truncated dodecahedron, and triangular prism cells, with a mirrored sphenoid vertex figure.
, has truncated icosidodecahedron, truncated dodecahedron, and triangular prism cells, with a mirrored sphenoid vertex figure.

Related honeycombs
| Image |  |
 |
 |
 |
|---|---|---|---|---|
| Symbols | tr{5,3,4} |
tr{4,3,5} |
tr{3,5,3} |
tr{5,3,5} |
| Vertex figure |
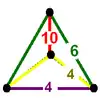 |
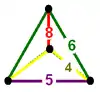 |
 |
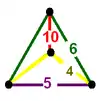 |
Runcinated icosahedral honeycomb
| Runcinated icosahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | t0,3{3,5,3} |
| Coxeter diagram | |
| Cells | {3,5} {}×{3} |
| Faces | triangle {3} square {4} |
| Vertex figure |  pentagonal antiprism |
| Coxeter group | , [[3,5,3]] |
| Properties | Vertex-transitive, edge-transitive |
The runcinated icosahedral honeycomb, t0,3{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has icosahedron and triangular prism cells, with a pentagonal antiprism vertex figure.
, has icosahedron and triangular prism cells, with a pentagonal antiprism vertex figure.

- Viewed from center of triangular prism
Related honeycombs
| Image |  |
 |
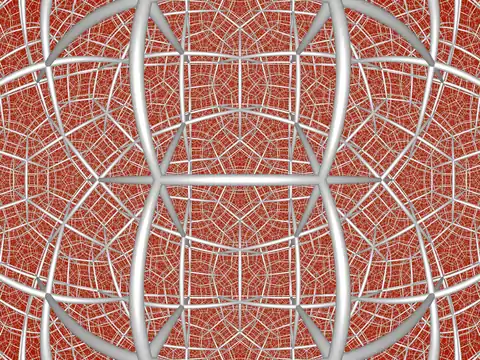 |
|---|---|---|---|
| Symbols | t0,3{4,3,5} |
t0,3{3,5,3} |
t0,3{5,3,5} |
| Vertex figure |
 |
 |
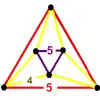 |
Runcitruncated icosahedral honeycomb
| Runcitruncated icosahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | t0,1,3{3,5,3} |
| Coxeter diagram | |
| Cells | t{3,5} rr{3,5} {}×{3} {}×{6} |
| Faces | triangle {3} square {4} pentagon {5} hexagon {6} |
| Vertex figure |  isosceles-trapezoidal pyramid |
| Coxeter group | , [3,5,3] |
| Properties | Vertex-transitive |
The runcitruncated icosahedral honeycomb, t0,1,3{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has truncated icosahedron, rhombicosidodecahedron, hexagonal prism, and triangular prism cells, with an isosceles-trapezoidal pyramid vertex figure.
, has truncated icosahedron, rhombicosidodecahedron, hexagonal prism, and triangular prism cells, with an isosceles-trapezoidal pyramid vertex figure.
The runcicantellated icosahedral honeycomb is equivalent to the runcitruncated icosahedral honeycomb.

- Viewed from center of triangular prism
Related honeycombs
| Four runcitruncated regular compact honeycombs in H3 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Omnitruncated icosahedral honeycomb
| Omnitruncated icosahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | t0,1,2,3{3,5,3} |
| Coxeter diagram | |
| Cells | tr{3,5} {}×{6} |
| Faces | square {4} hexagon {6} dodecagon {10} |
| Vertex figure | 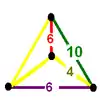 phyllic disphenoid |
| Coxeter group | , [[3,5,3]] |
| Properties | Vertex-transitive |
The omnitruncated icosahedral honeycomb, t0,1,2,3{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has truncated icosidodecahedron and hexagonal prism cells, with a phyllic disphenoid vertex figure.
, has truncated icosidodecahedron and hexagonal prism cells, with a phyllic disphenoid vertex figure.

- Centered on hexagonal prism
Related honeycombs
| Three omnitruncated regular compact honeycombs in H3 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Omnisnub icosahedral honeycomb
| Omnisnub icosahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs in hyperbolic space |
| Schläfli symbol | h(t0,1,2,3{3,5,3}) |
| Coxeter diagram | |
| Cells | sr{3,5} s{2,3} irr. {3,3} |
| Faces | triangle {3} pentagon {5} |
| Vertex figure | 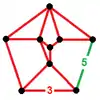 |
| Coxeter group | [[3,5,3]]+ |
| Properties | Vertex-transitive |
The omnisnub icosahedral honeycomb, h(t0,1,2,3{3,5,3}), ![]()
![]()
![]()
![]()
![]()
![]()
![]() , has snub dodecahedron, octahedron, and tetrahedron cells, with an irregular vertex figure. It is vertex-transitive, but cannot be made with uniform cells.
, has snub dodecahedron, octahedron, and tetrahedron cells, with an irregular vertex figure. It is vertex-transitive, but cannot be made with uniform cells.
Partially diminished icosahedral honeycomb
| Partially diminished icosahedral honeycomb Parabidiminished icosahedral honeycomb | |
|---|---|
| Type | Uniform honeycombs |
| Schläfli symbol | pd{3,5,3} |
| Coxeter diagram | - |
| Cells | {5,3} s{2,5} |
| Faces | triangle {3} pentagon {5} |
| Vertex figure | 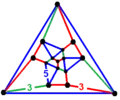 tetrahedrally diminished dodecahedron |
| Coxeter group | 1/5[3,5,3]+ |
| Properties | Vertex-transitive |
The partially diminished icosahedral honeycomb or parabidiminished icosahedral honeycomb, pd{3,5,3}, is a non-Wythoffian uniform honeycomb with dodecahedron and pentagonal antiprism cells, with a tetrahedrally diminished dodecahedron vertex figure. The icosahedral cells of the {3,5,3} are diminished at opposite vertices (parabidiminished), leaving a pentagonal antiprism (parabidiminished icosahedron) core, and creating new dodecahedron cells above and below.[1][2]


See also
References
- Wendy Y. Krieger, Walls and bridges: The view from six dimensions, Symmetry: Culture and Science Volume 16, Number 2, pages 171–192 (2005) Archived 2013-10-07 at the Wayback Machine
- "Pd{3,5,3".}
- Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
- Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999 ISBN 0-486-40919-8 (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables II,III,IV,V, p212-213)
- Norman Johnson Uniform Polytopes, Manuscript
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- N.W. Johnson: Geometries and Transformations, (2018) Chapter 13: Hyperbolic Coxeter groups
- Klitzing, Richard. "Hyperbolic H3 honeycombs hyperbolic order 3 icosahedral tesselation".