Run-and-tumble motion

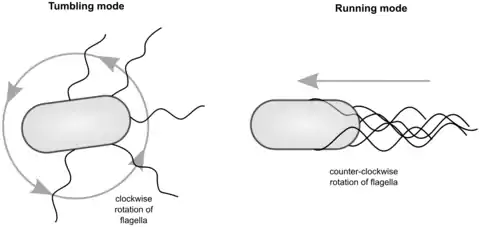
Many bacteria swim, propelled by rotation of the flagella outside the cell body. In contrast to protist flagella, bacterial flagella are rotors and—irrespective of species and type of flagellation—they have only two modes of operation: clockwise or counterclockwise rotation. Bacterial swimming is used in bacterial taxis (mediated by specific receptors and signal transduction pathways) for the bacterium to move in a directed manner along gradients and reach more favorable conditions for life.[3][4] The direction of flagellar rotation is controlled by the type of molecules detected by the receptors on the surface of the cell: in the presence of an attractant gradient, the rate of smooth swimming increases, while the presence of a repellent gradient increases the rate of tumbling.[1][5]

Run-and-tumble motion is found in many peritrichous bacteria, including E. coli, Salmonella typhimurium, and Bacillus subtilis.[6] It has also been observed in the alga Chlamydomonas reinhardtii[7] and the cyanobacterium Synechocystis.[8]

Escherichia coli

An archetype of bacterial swimming is represented by the well-studied model organism Escherichia coli.[5] With its peritrichous flagellation, E. coli performs a run-and-tumble swimming pattern, as shown in the diagrams below. Counterclockwise rotation of the flagellar motors leads to flagellar bundle formation that pushes the cell in a forward run, parallel to the long axis of the cell. Clockwise rotation disassembles the bundle and the cell rotates randomly (tumbling). After the tumbling event, straight swimming is recovered in a new direction.[1] That is, counterclockwise rotation results in steady motion and clockwise rotation in tumbling; counterclockwise rotation in a given direction is maintained longer in the presence of molecules of interest (like sugars or aminoacids).[1][5]

E. coli have flagella which project in all directions. Clockwise (CW) rotation of flagellar motors results in random re-orientation for the bacterium, but counter-clockwise (CCW) rotation produces approximate straight-line motion.[10]

Run-and-tumble swimming pattern [5]

Diagram of E. coli, with flagella projecting in all directions

In a uniform medium, run-and-tumble trajectories appear as a sequence of nearly straight segments interspersed by erratic reorientation events, during which the bacterium remains stationary. The straight segments correspond to the runs, and the reorientation events correspond to the tumbles. Because they exist at low Reynolds number, bacteria starting at rest quickly reach a fixed terminal velocity, so the runs can be approximated as constant velocity motion. The deviation of real-world runs from straight lines is usually attributed to rotational diffusion, which causes small fluctuations in the orientation over the course of a run.

In contrast with the more gradual effect of rotational diffusion, the change in orientation (turn angle) during a tumble is large; for an isolated E. Coli in a uniform aqueous medium, the mean turn angle is about 70 degrees, with a relatively broad distribution. In more complex environments, the tumbling distribution and run duration may depend on the agent's local environment, which allows for goal-oriented navigation (taxis).[11][12] For example, a tumbling distribution that depends on a chemical gradient can guide bacteria toward a food source or away from a repellant, a behavior referred to as chemotaxis.[13] Tumbles are typically faster than runs: tumbling events of E. Coli last about 0.1 seconds, compared to ~ 1 second for a run.

Synechocystis

Synechocystis

Cross section of a Synechocystis cell with pili. These cells lack flagella, but achieve motility using retractile type IV pili [14]

Run-and-tumble motion of a Synechocystis cyanobacterium. During run the cell moves quickly from one point to another, while during tumble it remains constrained in a given area and tends to change directions.[8]

Another example is Synechocystis, a genus of cyanobacterium. Cyanobacterium do not have flagella. Nonetheless, Synechocystis species can move in cell suspensions and on moist surfaces and by using retractile type IV pili, displaying an intermittent two phase motion; a high-motility run and a low-motility tumble (see diagram).[14][15] The two phases can be modified under various external stressors. Increasing the light intensity, uniformly over the space, increases the probability of Synechocystis being in the run state randomly in all directions. This feature, however, vanishes after a typical characteristic time of about one hour, when the initial probability is recovered. These results were well described by a mathematical model based on a linear response theory proposed by Vourc’h et al.[15][8]

Synechocystis cells can also undergo biased motility under directional illumination. Under directional light flux, Synehcocystis cells perform phototactic motility and head toward the light source (in positive phototaxis). Vourc’h et al. (2020) showed that this biased motility stems from the averaged displacements during run periods, which is no longer random (as it was in the uniform illumination).[15] They showed the bias is the result of the number of runs, which is greater toward the light source, and not of longer runs in this direction.[15] Brought together, these results suggest distinct pathways for the recognition of light intensity and light direction in this prokaryotic microorganism. This effect can be used in the active control of bacterial flows.[8]

It has also been observed that very strong local illumination inactivates the motility apparatus.[16] Increasing the light intensity of more than ~475 µmol m⁻² s⁻¹ reverses the direction of Synechocystis cells to move away from the high levels of radiation source.[17][18] Moreover, Synechocystis cells show a negative phototaxis behavior under ultraviolet radiation as an effective escape mechanism to avoid damage to DNA and other cellular components of Synechocystis.[19][18][20][8] Contrary to the run phase that can extend from a fraction of a second to several minutes, the tumble lasts only a fraction of a second. The tumbling phase is a clockwise rotation that allows the cell to change the motility direction of the next run.[21][22][8]

Chemotaxis is another scheme that allows an organism to move toward or away from gradients of nutrients or other chemical stimuli. Detecting by transmembrane chemoreceptors [23][24][25] the microorganism performs a three-dimensional random walk is observed in a homogenous environment, and the direction of each run is identified after a tumble.[21][8]

Theoretically and computationally, run-and-tumble motion can be modeled as a stochastic process. One of the simplest models is based on the following assumptions:[26][27]

• Runs are straight and performed at constant velocity v₀ (initial speed-up is instantaneous)
• Tumbling events are uncorrelated and occur at average rate α, i.e., the number of tumbling events in a given time interval has a Poisson distribution. This implies that the run durations are exponentially distributed with mean α⁻¹.
• Tumble duration is negligible
• Interactions with other agents are negligible (dilute limit)

With a few other simplifying assumptions, an integro-differential equation can be derived for the probability density function f (r, ŝ, t), where r is the particle position and ŝ is the unit vector in the direction of its orientation. In d-dimensions, this equation is

${\displaystyle {\frac {\partial f(\mathbf {r} ,{\hat {\mathbf {s} }},t)}{\partial t}}+v_{0}\,{\hat {\mathbf {s} }}\cdot \nabla f(\mathbf {r} ,{\hat {\mathbf {s} }},t)=\xi ^{-1}\nabla \cdot (\nabla V(\mathbf {r} )f(\mathbf {r} ,{\hat {\mathbf {s} }},t))-\alpha f(\mathbf {r} ,{\hat {\mathbf {s} }},t)+{\frac {\alpha }{\Omega _{d}}}\int g({\hat {\mathbf {s} }}-{\hat {\mathbf {s} }}')f(\mathbf {r} ,{\hat {\mathbf {s} }}',t)d{\hat {\mathbf {s} }}'}$

where Ω_d = 2π^d/2/Γ(d/2) is the d-dimensional solid angle, V(r) is an external potential, ξ is the friction, and the function g (ŝ - ŝ') is a scattering cross section describing transitions from orientation ŝ' to ŝ. For complete reorientation, g = 1. The integral is taken over all possible unit vectors, i.e., the d-dimensional unit sphere.

In free space (far from boundaries), the mean squared displacement ⟨r(t)²⟩ generically scales as ⟨r(t)²⟩ ~ t² for small t and ⟨r(t)²⟩ ~ t for large t. In two dimensions, the mean squared displacement corresponding to initial condition f (r, ŝ, 0) = δ(r)/(2π) is

${\displaystyle \langle \mathbf {r} ^{2}\rangle ={\frac {2v_{0}^{2}}{\alpha ^{2}(1-\sigma _{1})}}\left[\alpha \,t+{\frac {e^{-\alpha (1-\sigma _{1})t}-1}{1-\sigma _{1}}}\right]}$

where

${\displaystyle \sigma _{1}=\int _{0}^{2\pi }g({\hat {\mathbf {s} }})(\cos \theta )d\theta }$

with ŝ parametrized as ŝ = (cos θ, sin θ).[28]

In real-world systems, more complex models may be required. In such cases, specialized analysis methods have been developed to infer model parameters from experimental trajectory data.[29][30][31]

The mathematical abstraction of run-and-tumble motion also appears outside of biology—for example, in idealized models of radiative transfer and neutron transport.[32][33][34]